Calculus AB/BC – 6.6 Applying Properties of Definite Integrals

The Algebros

22 Dec 202015:39

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, Mr. Bean explores the properties of definite integrals, using visual examples to explain how to calculate the area under a curve. He covers the effects of reversing limits, constant multiplication, and the addition and subtraction of integrals. The video also touches on more complex topics like piecewise functions and absolute values, emphasizing the importance of practice and the use of a calculator for accurate calculations.

Takeaways

📚 Properties of definite integrals are explored, including the effects of changing limits and the impact of constants.
🔄 When the limits of integration are reversed, the sign of the integral changes, as demonstrated by the example of integrating from 0 to 12 versus from 12 to 0.
🎯 The area under a curve from a specific point to the same point (e.g., from a to a) results in zero, as there is no width in the interval.
🔢 Multiplying the function by a constant factor moves the constant to the front of the integral, following a similar rule to the constant rule in derivatives.
📈 The properties of integrals allow for breaking up the integration interval (e.g., from a to c and then from c to b) and adding the results.
➕ The addition and subtraction properties of integrals enable the separate calculation of integrals for different functions and the combination of their results.
🤔 Sometimes, based on the given information, it's not possible to determine the value of an integral, which is an acceptable answer on exams like the AP exam.
📊 Piecewise functions are treated like regular functions when calculating definite integrals; their geometric shapes are used to find the area under the curve.
🏷️ Absolute value functions create V-shaped graphs and are treated as piecewise functions, with the integral representing the area under the curve up to a certain point.
🧮 The use of a calculator is essential for calculating integrals, especially when the shapes are complex or not easily calculated by hand.
🛠️ Practice with a calculator is crucial for mastering the calculation of integrals, and students should familiarize themselves with the specific functions of their calculator model.

Q & A

What is the main topic of the video?
-The main topic of the video is the properties of definite integrals and how they can be used to calculate the area under a curve.
How does Mr. Bean introduce the concept of definite integrals in the video?
-Mr. Bean introduces the concept of definite integrals by discussing the area under a curve and using an example of a definite integral from 0 to 12, explaining how to account for areas under the x-axis.
What is the significance of reversing the limits of integration in the video's examples?
-Reversing the limits of integration changes the sign of the area under the curve. This is important because it affects how the area is calculated when moving from one point to another in the opposite direction.
What happens when the lower and upper limits of a definite integral are the same?
-When the lower and upper limits of a definite integral are the same, the area under the curve is zero, as there is no width to the region being integrated.
How does the video explain the property of multiplying a definite integral by a constant?
-The video explains that when a definite integral is multiplied by a constant, the constant can be factored out and brought to the front of the integral, similar to the constant rule with derivatives.
What is the rule for integrating over a piecewise function as explained in the video?
-The rule for integrating over a piecewise function is to treat each piece of the function separately, calculating the area under each piece and then summing these areas to find the total area under the curve.
How does the video demonstrate the difference between taking the absolute value of an integral and integrating the absolute value of a function?
-The video shows that taking the absolute value of an integral means calculating the integral and then taking the absolute value of the result, making all areas positive. In contrast, integrating the absolute value of a function means that the negative areas under the x-axis are flipped to become positive, changing the result significantly.
Why does Mr. Bean emphasize the use of a calculator for certain integrals in the video?
-Mr. Bean emphasizes the use of a calculator for certain integrals because it is a fast and easy way to calculate the area under the curve when a geometric approach is not straightforward or when the calculator is allowed in an exam setting.
What is the specific example given in the video for demonstrating the use of a calculator to find an integral?
-The specific example given is the integral of (x - 1) square root from 2 to 3. Mr. Bean demonstrates how to use a calculator to find this integral, showing that the result is approximately 1.218 or 1.219.
What advice does Mr. Bean give for practicing the concepts discussed in the video?
-Mr. Bean advises viewers to practice sketching graphs, understanding piecewise functions, and using a calculator to calculate integrals, especially when it is allowed in an exam setting.

Outlines

00:00

📚 Properties of Definite Integrals

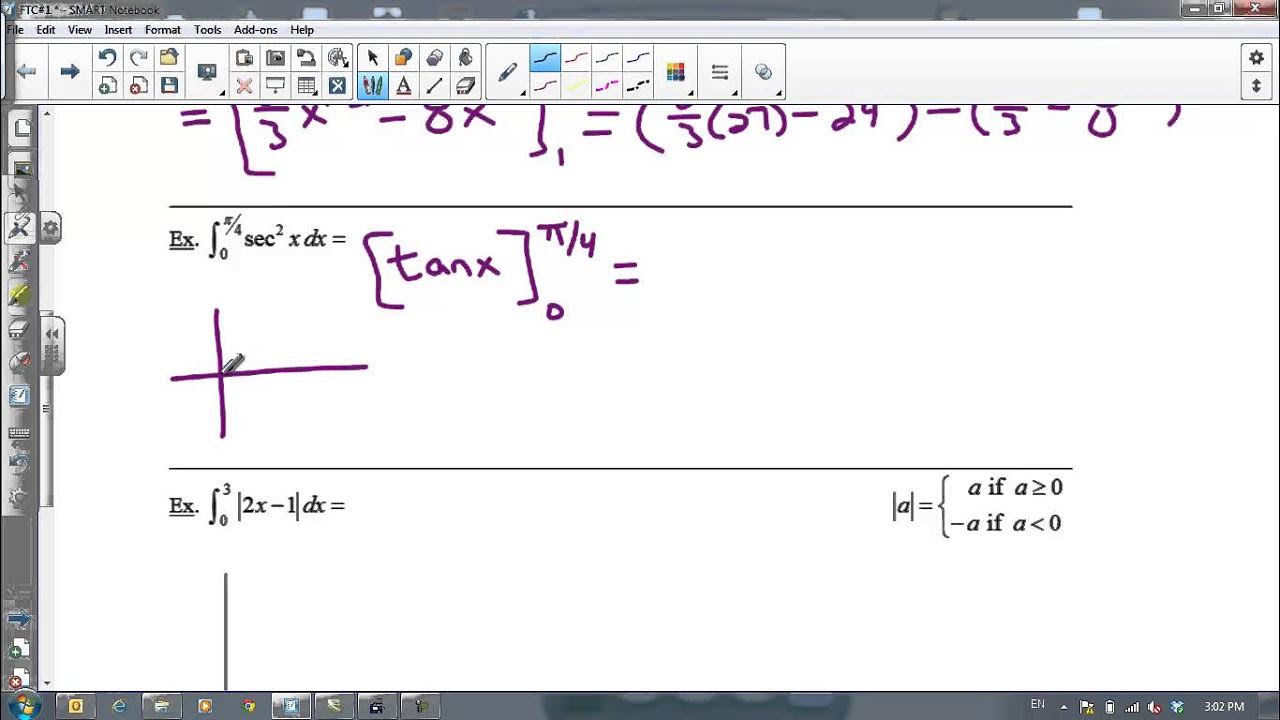
This paragraph introduces the properties of definite integrals, using examples to illustrate how integrals work with areas under curves. Mr. Bean explains how to calculate the area from 0 to 12 and how the area changes when the limits of integration are reversed. He also discusses the properties of integrals when the limits are the same (resulting in zero), and when constants are involved in the integration process. The concept of breaking down an integral into smaller parts (from a to c and then c to b) is also explained, along with the basic operations of addition and subtraction of integrals.

05:02

🔢 Solving Integrals with Different Limits

In this section, the speaker continues to explore definite integrals by demonstrating how to solve them when the limits of integration are different. He uses the properties of integrals to manipulate expressions and find solutions. The paragraph covers the calculation of integrals with negative limits, the addition of integrals from different intervals, and the concept of 'cannot be determined' when there's insufficient information. The speaker also introduces piecewise functions and explains how to calculate the area under such functions, emphasizing the importance of geometric understanding.

10:02

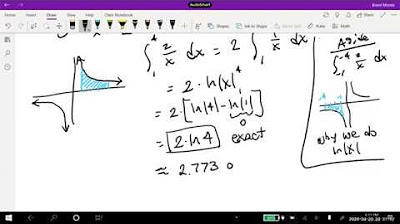
📊 Absolute Value Functions and Calculator Practice

This paragraph delves into the specifics of dealing with absolute value functions in the context of integration. The speaker clarifies the difference between taking the absolute value of an integral and integrating the absolute value of a function. He provides visual examples and explains how to interpret the results. Additionally, the speaker highlights the importance of calculator usage for solving integrals, especially when it's allowed, and guides through the process of using a calculator to find the area under a curve, specifically for a square root function over a given interval.

15:03

🎓 Mastery Check and Next Steps

The final paragraph wraps up the lesson with a mastery check, encouraging viewers to practice the concepts learned. The speaker advises on the use of calculators for quick and easy calculations of integrals, especially when they are allowed in assessments. He also previews upcoming lessons, hinting at more in-depth exploration of calculating areas under curves by hand, and encourages viewers to practice sketching graphs and using calculators to solidify their understanding of the material.

Mindmap

Keywords

💡Definite Integrals

Definite integrals are a mathematical concept used to calculate the area under a curve between two points on the x-axis. In the video, Mr. Bean introduces the properties of definite integrals and uses them to find areas under curves, starting with a basic example from 0 to 12 and then exploring more complex scenarios.

💡Properties of Integrals

The properties of integrals are rules that govern how integrals behave under various operations such as changing the order of integration, combining integrals, or dealing with constants. These properties are crucial for solving more complex integral problems and are discussed in the video, including the reversal of limits and the addition and subtraction of integrals.

💡Area Under the Curve

The area under the curve refers to the region enclosed by the graph of a function and the x-axis between two points. This concept is central to the understanding of definite integrals, as it represents the quantity being calculated. In the video, Mr. Bean uses this concept to explain how integrals can be visualized and calculated.

💡Piecewise Functions

A piecewise function is a function that is defined by different formulas for different parts of its domain. These functions can be more complex to integrate because the area under the curve may consist of multiple shapes. In the video, Mr. Bean demonstrates how to calculate the area under a piecewise function by breaking it down into simpler shapes.

💡Absolute Value Functions

Absolute value functions are mathematical functions that take a real number as an input and output the non-negative value of that number. In the context of the video, absolute value functions are discussed as piecewise functions, which can be visualized as V-shaped graphs and integrated using the properties of definite integrals.

💡Calculus

Calculus is a branch of mathematics that deals with rates of change and accumulation. It includes both differential calculus, which examines how quantities change as other quantities vary, and integral calculus, which focuses on finding accumulated quantities such as areas under curves. The video's content is centered around integral calculus.

💡Limits

In calculus, limits are used to describe the behavior of a function as the input (or another variable) approaches a certain value. In the context of definite integrals, the limits define the interval under the curve that is being integrated. The video discusses how changing the limits affects the calculation of the integral.

💡Constant Multiplication

Constant multiplication is a property of integrals that states a constant factor can be pulled out in front of the integral sign. This simplifies the calculation by allowing the constant to be multiplied by the result of the integral, rather than having to be integrated term by term.

💡Geometry

Geometry is the branch of mathematics concerned with the properties and relations of points, lines, angles, surfaces, and solids. In the context of the video, geometry is used to visualize and calculate the areas under curves, which are the integrals.

💡Calculator

A calculator is an electronic device used to perform mathematical calculations. In the video, Mr. Bean emphasizes the importance of practicing the use of a calculator for calculating integrals, especially when it is allowed in an exam setting.

💡Master Check

A master check is a term used in the context of the video to refer to a practice test or a review session that students can use to assess their understanding of the material covered in the lesson. It is a tool for mastery and reinforcement of the concepts learned.

Highlights

Introduction to the properties of definite integrals and their applications.

Explanation of how the area under a curve can be calculated using definite integrals.

Illustration of how the definite integral from 0 to 12 is computed.

Discussion on reversing limits of integration and the resulting change in sign of the integral.

Explanation of what happens when the lower and upper limits of integration are the same.

Clarification on multiplying the integral by a constant and the effect it has on the result.

Demonstration of how to break down an integral into smaller parts when the limits are not in order.

Introduction to the property of addition for integrals and how to apply it.

Explanation of the subtraction property for integrals and its application.

Example of how to deal with piecewise functions in the context of integration.

Discussion on the treatment of absolute value functions in integration.

Explanation of the difference between taking the absolute value of the integral and integrating the absolute value of a function.

Emphasis on the importance of practicing the calculation of integrals using a calculator.

Demonstration of how to use a calculator to find the area under a curve defined by a function.

Explanation of the graphical approach to understanding the area under the curve of a square root function.

Conclusion and encouragement to practice the concepts learned in the lesson.

Transcripts

Browse More Related Video

Calculus AB/BC – 6.4 The Fundamental Theorem of Calculus and Accumulation Functions

Calculus AB/BC – 6.7 The Fundamental Theorem of Calculus and Definite Integrals

Fundamental Theorem of Calculus

Riemann Sums and Definite Integrals

Math 11 - Section 4.3

Math 1325 Lecture 13 2