Tensor Calculus Lecture 15: Geodesic Curvature Preview
TLDRThis video delves into the relationship between curves and surfaces in differential geometry, focusing on the curvature normal and its interpretation. The script explores the formula that links the behavior of a curve embedded in a surface to the ambient Euclidean space, highlighting the concepts of principal curvatures, Gaussian curvature, and geodesic curvature. The presenter uses an apple to intuitively demonstrate how the geodesic, the shortest path between two points on a surface, has zero geodesic curvature, illustrating the fundamental role of curvature in determining the shortest distances on a surface.
Takeaways
- 📚 The video script discusses differential geometry and tensor calculus, focusing on the relationship between curves and surfaces in an ambient Euclidean space.
- 🧩 It revisits a complex formula that connects various aspects of curves embedded in surfaces, emphasizing the importance of understanding the behavior of both the curve and the surface.
- 🔍 The script introduces the concept of principal curvatures and Gaussian curvature, using a derived formula to explain these geometric properties.
- 📐 The 'V alpha beta' term from the formula represents the curvature tensor for the surface in the Euclidean space, which is key to understanding the surface's curvature.
- 🌐 The 'geodesic curvature' is highlighted as the main focus of the video, explaining it as the mean curvature for a curve embedded in a surface.
- 📈 The script explains how to construct the curvature tensor for a curve embedded in a surface by applying the same logic used for a surface in Euclidean space, but with adjustments for the curved space.
- 📉 The 'curvature normal' is described as an invariant vector that represents the rate of change of the unit tangent vector along the curve, providing an intuitive understanding of curvature.
- 🌀 The script uses an analogy of a spiral to illustrate the concept of the curvature normal being orthogonal to the axis of the spiral, helping to visualize the concept.
- 📍 The formula presented in the script decomposes the curvature normal into components related to the surface normal and the tangential normal, providing a deeper understanding of the curve's embedding.
- 🌍 The concept of 'geodesic' is introduced as the shortest path between two points on a surface, with the script suggesting that the geodesic curvature is zero for the shortest path.
- 🍏 An intuitive demonstration using an apple as a curved surface helps to visualize the geodesic and its curvature, emphasizing the idea that the geodesic curvature vanishes for the shortest path.
Q & A
What is the main topic of discussion in the video script?
-The main topic of discussion in the video script is the relationship between the curvatures of a curve embedded in a surface and the surface itself, with a focus on differential geometry and tensor calculus.
What is the significance of the formula derived in the last video?
-The formula derived in the last video is significant as it relates the behavior of a curve with the behavior of the surface in which it is embedded, connecting various aspects of curvatures in the context of differential geometry.
What are the two main normals mentioned in the script when discussing an embedded curve?
-The two main normals mentioned are the unit normal of the surface (denoted as n) and the tangential normal of the curve (denoted as little n), which lies in the plane tangential to the surface.
What is the curvature tensor V_alpha_beta mentioned in the script?
-V_alpha_beta is the curvature tensor for the surface as embedded in the overall Euclidean space, representing the curvature normal, which is a key concept in the script's discussion.
What is the geodesic curvature and why is it the focus of the video?
-The geodesic curvature is the curvature tensor or mean curvature for the curve as embedded in the surface. It is the focus of the video because it provides an intuitive understanding of how curves behave when embedded in surfaces and is central to the concept of shortest paths or geodesics.
How is the curvature normal related to the rate of change of the unit tangent vector along a curve?
-The curvature normal is directly related to the rate of change of the unit tangent vector along a curve, representing the vector rate of change that points inward and is proportional to the curvature of the curve.
What is the physical interpretation of the curvature normal?
-The physical interpretation of the curvature normal is the acceleration of a material particle moving along the curve with unit speed, where the derivative points in the direction of the inward normal to the curve.
How does the script relate the curvature normal to the surface normal and the tangential normal?
-The script explains that the curvature normal can be decomposed into components along the surface normal and the tangential normal, expressing any vector orthogonal to the curve as a linear combination of these two normals.
What is the concept of principal curvatures mentioned in the script?
-Principal curvatures are the components of the curvature normal in the direction normal to the surface, leading to the concept of in-plane or tangential curvature, which is part of the analysis of the curve embedded in the surface.
Why is the geodesic curvature considered to be zero for the shortest path between two points on a surface?
-The geodesic curvature is considered to be zero for the shortest path, or geodesic, because this path does not meander and goes straight over the surface, lacking an in-plane component to its curvature normal, thus making the total geodesic curvature zero.
How does the script use an apple to illustrate the concept of geodesics and curvature normals?
-The script uses an apple as a curved surface to visually demonstrate the shortest path between two points (geodesic) and how the curvature normal aligns with the surface normal for this path, indicating zero geodesic curvature.
Outlines
📚 Introduction to Differential Geometry and Tensor Calculus
The speaker returns to the topic of differential geometry and tensor calculus after a break, focusing on the relationship between curves and surfaces in Euclidean space. They introduce the concept of principal curvatures and Gaussian curvature, reminding viewers of a previously derived formula that connects the behavior of a curve embedded in a surface to the behavior of the surface itself. The formula is explained in the context of a surface in an ambient Euclidean space, with the curve having its own normal vector, tangential to the surface. The speaker also discusses the curvature tensor for the surface and the geodesic curvature, which is central to the video's theme.
🔍 Exploring Curvature Normals and Their Intuitive Interpretation
This paragraph delves into the concept of curvature normals, which represent the rate of change of the unit tangent vector along a curve. The speaker uses a simple analogy with a phone to illustrate how the curvature normal points inward and is proportional to the curve's steepness. They explain that the curvature normal can be decomposed into components related to the surface and the curve's embedding, leading to the idea of principal curvatures. The paragraph also touches on the concept of geodesics, the shortest paths between points on a surface, and their connection to zero geodesic curvature, suggesting an intuitive understanding of why geodesics are characterized by minimal curvature.
🌐 Geodesics and the Intuitive Link to Zero Curvature
The speaker uses an apple as a model for a curved surface to explain the concept of geodesics as the shortest paths between two points on a surface. They argue intuitively that the curvature normal for a geodesic should be aligned with the surface's normal, implying that the in-plane component of the curvature normal is zero for geodesics. This results in the geodesic curvature being zero, which is a key point in understanding the relationship between shortest distances on a surface and the curvature properties of that surface. The paragraph aims to provide a visual and intuitive grasp of why geodesics are significant in the study of surfaces and their curvature.
Mindmap
Keywords
💡Differential Geometry
💡Tensor Calculus
💡Principal Curvatures
💡Gaussian Curvature
💡Euclidean Space
💡Curve Embedded in a Surface
💡Tangential Normal
💡Curvature Tensor
💡Geodesic Curvature
💡Curvature Normal
💡Geodesic
Highlights
Introduction to the continuation of the discussion on differential geometry and tensor calculus.
Derivation of a formula connecting the behavior of a curve with the surface it is embedded in.
Explanation of the complex situation involving a surface in Euclidean space and a curve within that surface.
Introduction of principal curvatures and Gaussian curvature as part of the formula.
Discussion on the curve embedded in the surface as a hypersurface with its own normal.
Introduction of the geodesic curvature as the main focus of the video.
Vector form representation of the identity relating curvatures for clarity.
Explanation of the curvature tensor for the surface in Euclidean space.
Construction of the curvature tensor for a curve embedded in a surface.
Differentiation between the curvature normal and geodesic curvature.
Visual representation of the curvature normal as the rate of change of the unit tangent vector.
Intuitive understanding of the curvature normal as the physical acceleration of a material particle.
Decomposition of the curvature normal into components using the surface normal and the tangential normal.
Concept of geodesics as the shortest path between two points on a surface.
Intuitive explanation of geodesic curvature being zero for the shortest path.
Demonstration using an apple to visualize the concept of geodesics and their curvature.
Final intuition that the geodesic curvature vanishes for minimal curves, known as geodesics.
Transcripts
Browse More Related Video
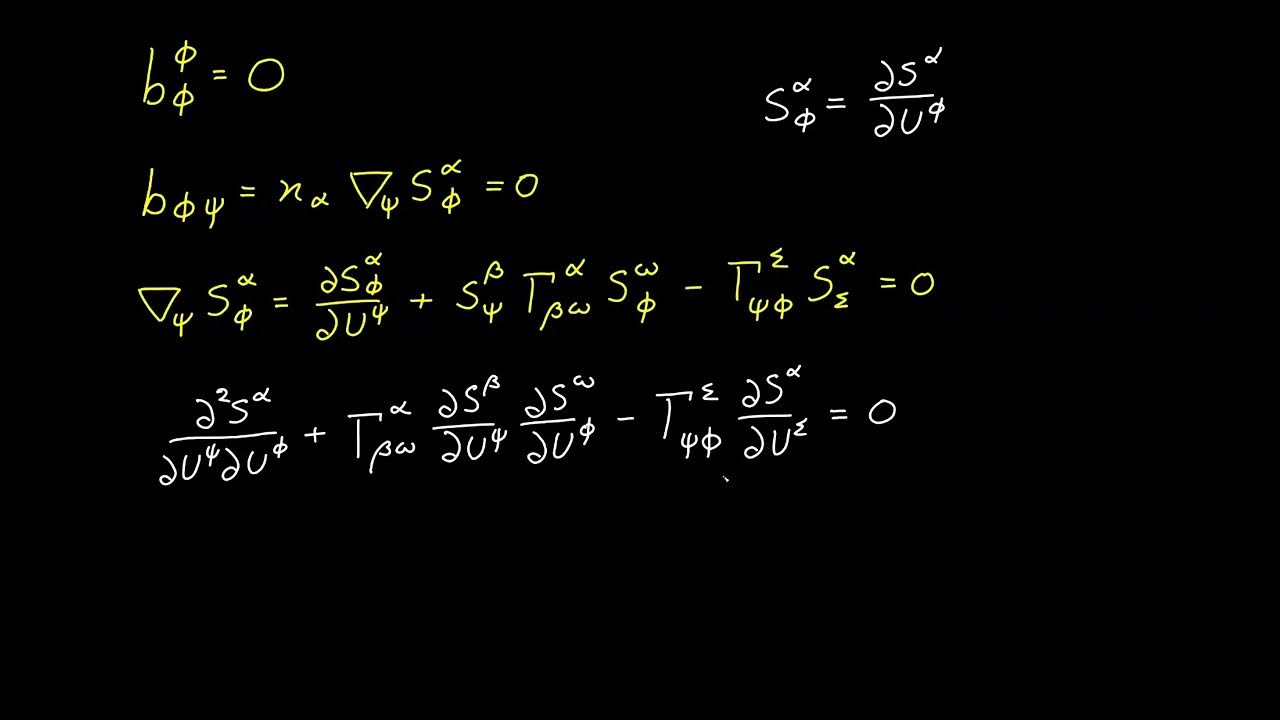
Video 95 - Geodesic Curves

Video 93 - Geodesic Curvature Tensor
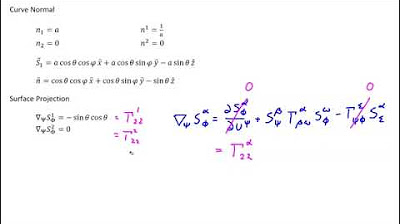
Video 94 - Sample Embedded Curve
Video 90 - Embedded Curves - Part 2

Tensor Calculus Lecture 14e: Non-hypersurfaces - Relationship Among Curvature Tensors 2

Tensor Calculus Lecture 14c: Non-hypersurfaces - Relationship Among The Shift Tensors
5.0 / 5 (0 votes)
Thanks for rating: