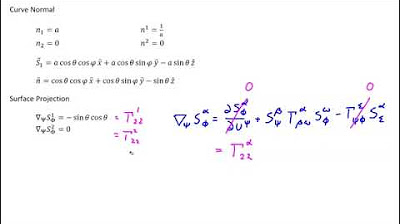Video 90 - Embedded Curves - Part 2
TLDRThis video, the 90th in a series on tensor calculus, continues the exploration of surface analysis applied to curves. It delves into the vector curvature normal, its relationship with the Laplacian of the position vector, and its expression as the product of curvature and the principal normal. The video draws parallels between surface and curve analysis, highlighting that all curves are intrinsically flat, with no intrinsic curvature like Gaussian curvature in surfaces. The script concludes with a detailed example of analyzing a spiral curve, demonstrating concepts such as the unit tangent vector, curvature, and the principal normal.
Takeaways
- 📚 The video is part of a series on tensor calculus, focusing on completing the review of surface analysis as it applies to curves.
- 🔍 The vector curvature normal is defined and shown to be equal to the Laplacian of the position vector, with alternate forms presented for evaluation using curve coordinates.
- 📈 The vector curvature normal is analogous to the mean curvature in surface analysis, representing a projection away from the manifold.
- 🔗 The Christoffel symbols for curves are simplified due to the nature of having only one index value, leading to a single Christoffel symbol for the curve.
- 📐 The covariant derivative for a curve is defined similarly to that for a surface, with specific attention to vectors lying on the manifold (tangent to the curve).
- 📉 The metric objects for a curve are metronomic, except for the basis vectors, which have non-zero covariant derivatives related to the principal normal.
- 🧩 The Laplacian for a curve, when applied to an invariant object, simplifies to the second derivative with respect to arc length, a property used in analyzing the vector curvature normal.
- 🔍 For a curve, the Riemann Christoffel tensor has only one component, which is equal to zero, indicating that all curves are intrinsically flat with no intrinsic curvature.
- 🌐 The analysis of a curve can be achieved by applying surface relationships, limiting Greek index values to 1 and replacing the surface normal with the principal normal.
- 🌀 A specific example of a spiral curve is used to demonstrate the application of the concepts discussed, including the calculation of various tensors and vectors.
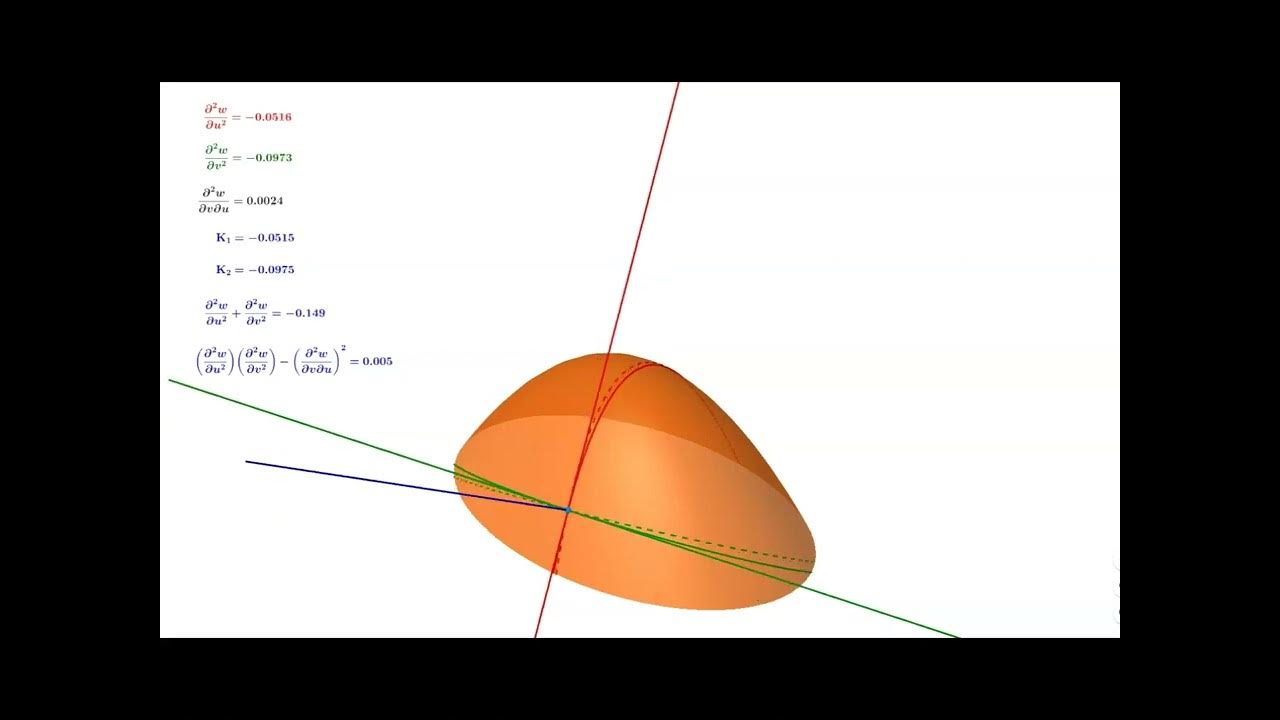
- 📉 The curvature of the spiral decreases as it moves outward, as the curve sweeps larger circles, which is visualized through the changing numerical value of curvature along the curve.
Q & A
What is the main focus of this video in the series on tensor calculus?
-The main focus of this video is to complete the review of surface analysis as it applies to curves, specifically by analyzing the vector curvature normal and its various representations.
What is the vector curvature normal in the context of this video?
-The vector curvature normal is a new object in the analysis that is equal to the Laplacian of the position vector and can be represented in several alternate forms using curve coordinates.
How is the vector curvature normal related to the curvature and the principal normal?
-The vector curvature normal is equal to the product of the curvature and the principal normal, which are both defined in a previous video, and it can be expressed as the product of the magnitude of this vector times the principal normal.
What is the mean curvature in the context of surface analysis?
-The mean curvature is a contraction of the curvature tensor, which is also equal to the sum of the principal curvatures of the surface, as discussed in a previous video.
How does the vector curvature normal's magnitude relate to the curvature of the line?
-The magnitude of the vector curvature normal is simply the curvature of the line, indicating the degree to which the curve deviates from being a straight line.
What is the Christoffel symbol and how does it apply to curves?
-The Christoffel symbol is a concept from differential geometry that describes the rate at which one vector field changes with respect to another. For a curve, there is only one Christoffel symbol, simplifying calculations as all indexes have to be a value of one.
What is the covariant derivative and how is it defined for a curve?
-The covariant derivative is a generalization of the derivative to curved spaces. For a curve, it is defined in the same form as for a surface but is limited to vectors that lie on the manifold, specifically tangent to the curve.
What is the significance of the Laplacian in the context of curves?
-For a curve, if the object is an invariant object, the Laplacian will always resolve to the equivalent of the second derivative of that object with respect to the arc length of the curve, providing a measure of how the object changes along the curve.
Why are all curves intrinsically flat according to the Riemann-Christoffel tensor?
-All curves are intrinsically flat because the Riemann-Christoffel tensor has only one component for a curve, and that component is equal to zero, indicating no intrinsic curvature.
What is the process of analyzing a curve in terms of surface relationships?
-To analyze a curve, one must apply the surface relationships derived earlier, limiting the values of the Greek indexes to 1 and replacing the surface normal n-hat with the principal normal p-hat.
Can you provide an example of how the concepts discussed are applied to a specific curve?
-The video provides a detailed example of analyzing a spiral curve, including deriving the parametric equations, shift tensor, covariant basis vector, covariant metric tensor, volume element, contravariant metric tensor, and other properties such as the unit tangent vector, curvature, and principal normal.
Outlines
📚 Completing Surface Analysis for Curves
This paragraph wraps up the discussion on surface analysis as it pertains to curves, following from video 88. The focus is on the vector curvature normal, which is identified as the Laplacian of the position vector and is shown to have multiple representations. The paragraph explains how the vector curvature normal can be evaluated using curve coordinates and how it relates to the curvature and the principal normal, concepts introduced in a previous video. It also draws an analogy between the vector curvature normal and the mean curvature from surface analysis, highlighting the projection away from the manifold in both cases. The paragraph concludes with a transition to further analysis of surface relationships as they apply to curves, starting with the Christoffel symbol and its properties.
🔍 Analyzing Curves Using Surface Relationships
The second paragraph delves into the application of surface analysis principles to curves, simplifying the process by limiting the indices to a value of one. It discusses the Christoffel symbol for curves, showing that there is only one such symbol due to the nature of curves, and demonstrates how to derive it and the second kind of Christoffel symbol. The paragraph also covers the covariant derivative, its definitions, and how it applies to vectors lying on the manifold, with specific attention to the tangential nature of these vectors for both surfaces and curves. The metronomic property of metric objects, the definition of the contravariant derivative, and the Laplacian for curves are also explained, emphasizing the intrinsic flatness of all curves due to the Riemann Christoffel tensor's sole component being zero.
🌀 Parametric Equations and Tensors for a Spiral
This paragraph introduces a specific example of a curve—a spiral—and outlines the process of assigning a parameter, identifying ambient coordinates, and deriving parametric equations that relate the curve coordinate to the ambient Cartesian coordinates. It then moves on to calculate the shift tensor, covariant basis vector, covariant metric tensor, and volume element for the spiral, highlighting the unique characteristics of these tensors for a curve, such as the single column in the shift tensor and the single component in the covariant metric tensor. The paragraph also covers the calculation of the contravariant metric tensor, the inverse shift tensor, and the metric equation, which leads to the expression for the arc length of the curve.
📐 Deriving Geometric Properties of a Spiral
The fourth paragraph continues the analysis of the spiral curve by deriving its unit tangent vector, vector curvature normal, curvature, and principal normal. It explains the process of finding the derivative of the unit tangent vector with respect to the curve coordinate and how to adjust this derivative to obtain the vector curvature normal. The curvature is calculated as the magnitude of this vector, and the principal normal is determined by dividing the vector curvature normal by its magnitude. The paragraph emphasizes the importance of understanding these calculations and encourages a review of the process at one's own pace.
📊 Visualizing Curvature and Tangent Vectors of a Spiral
The final paragraph provides a visual demonstration of the spiral curve, showing how various geometric properties change as a point moves along the curve. It discusses the relationship between the curve parameter and the Euclidean distance from the origin, the covariant basis vector's length and its tangential nature, and the unit tangent vector's constant length. The paragraph also introduces the contravariant basis vector, whose length is the reciprocal of the covariant basis vector's length, and the principal normal, which is perpendicular to the unit tangent vector and lies in the curvature plane. The curvature value is visualized, showing how it decreases as the curve extends outward. The paragraph concludes with a preview of the next video's topic, the Frenet formulas.
Mindmap
Keywords
💡Tensor Calculus
💡Vector Curvature Normal
💡Laplacian
💡Curvature
💡Principal Normal
💡Christoffel Symbols
💡Covariant Derivative
💡Metric Tensor
💡Riemann Curvature Tensor
💡Frenet Formulas
💡Arc Length
Highlights
Introduction of the vector curvature normal, a key object in the study of curves, which is analogous to the mean curvature in surface analysis.
Explanation of the vector curvature normal as the Laplacian of the position vector, providing an alternate form for evaluation using curve coordinates.
Demonstration that the vector curvature normal equals the product of curvature and the principal normal, emphasizing its geometric interpretation.
Analogy between the vector curvature normal and the mean curvature tensor in surface analysis, highlighting the projection away from the manifold.
Simplification of the Christoffel symbols for curves, showing that there is only one Christoffel symbol due to the limitation of index values.
Derivation of the covariant derivative for curves, including its application to vectors lying on the manifold and the use of the chain rule.
Metronomic property for curves, revealing that all metric objects are metronomic except for the basis vectors, which have non-zero covariant derivatives.
Definition and properties of the contravariant derivative and Laplacian for curves, emphasizing their straightforward application from surface analysis.
Special case of the Laplacian for curves, showing that for invariant objects, it resolves to the second derivative with respect to arc length.
Introduction of the Riemann-Christoffel tensor for curves, and the unique property that it has only one component which is zero, indicating that all curves are intrinsically flat.
Geometric interpretation of the intrinsic flatness of curves, explaining that curves can be parameterized by arc length and appear as Euclidean spaces.
Application of surface relationships to curves by limiting Greek index values to 1 and replacing the surface normal with the principal normal.
Example analysis of a spiral curve, including parameter assignment, parametric equations, and the shift tensor.
Derivation of the covariant basis vector, covariant metric tensor, and volume element for the spiral curve.
Calculation of the contravariant metric tensor and the magnitude of the contravariant basis vectors for the curve.
Determination of the inverse shift tensor and the metric equation for the spiral curve, leading to the arc length expression.
Derivation of the Christoffel symbols for the spiral curve, showcasing the ease of finding these symbols due to the single index limitation.
Calculation of the unit tangent vector for the spiral, illustrating its relationship with the covariant basis vector and the volume element.
Determination of the vector curvature normal, curvature, and principal normal for the spiral curve, providing a comprehensive understanding of its geometric properties.
Visual demonstration of the spiral curve's properties, including coordinates, arc length, line element, and basis vectors.
Conclusion and preview of the next video, which will introduce the Frenet formulas for curves.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: