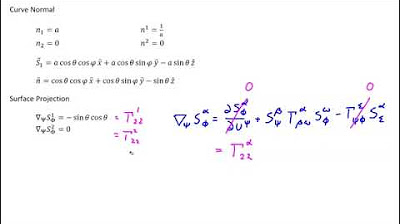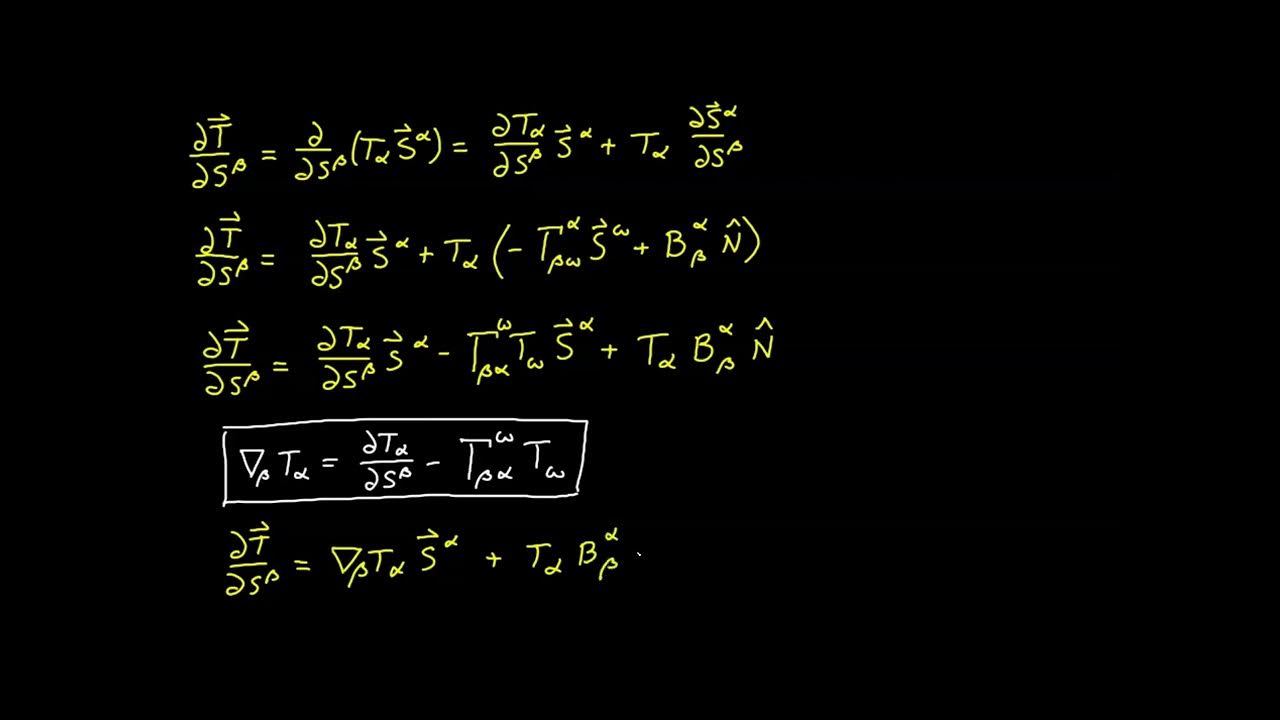Video 89 - Curve Projections
TLDRIn this video on tensor calculus, the decomposition of vectors into projections is explored, highlighting the differences between curves and surfaces. The covariant derivative and Christoffel symbols are discussed, with an emphasis on their application to flat and curved surfaces. The video delves into the projection of partial derivatives onto tangent planes and introduces the curvature tensor. It also examines the analogous process for curves, introducing the vector curvature normal and its relationship to the curvature of a line, providing a foundation for further exploration in subsequent videos.
Takeaways
- 📚 The video script is a continuation of a series on tensor calculus, focusing on the decomposition of vectors into projections on curves and surfaces.
- 🔍 It begins with a review of the covariant derivative and the role of the Christoffel symbol in flat Euclidean manifolds, and how it does not apply to curved surfaces without modification.
- 📉 The script explains that the partial derivative on a curved surface may not lie in the tangent plane, necessitating a projection onto the tangent plane for a correct expression.
- 📐 An enhanced definition of the Christoffel symbol is introduced to represent the projection of the partial derivative onto the tangent plane.
- 📈 The script discusses the need for an additional term in the expression for the covariant derivative on a surface, involving the curvature tensor, to account for the normal component.
- 🧵 When analyzing curves, the script points out that the covariant derivative along a curve may result in a vector pointing in any direction, not just along the tangent line.
- 📊 The concept of a vector curvature normal is introduced for curves, which is similar to the curvature tensor for surfaces but involves a projection onto a plane perpendicular to the curve.
- 📘 The script derives expressions for the vector curvature normal and shows its relationship to the Laplacian of the position vector and the second derivative of the curve.
- 🔗 It is highlighted that the vector curvature normal is orthogonal to the contravariant basis vector, indicating it is perpendicular to the curve at a given point.
- 📚 The video script concludes by drawing parallels between the equations for surface manifolds and curves, emphasizing the role of the principal normal vector in curvature calculations for curves.
- 🔍 The takeaway is that the script provides a detailed mathematical exploration of tensor calculus concepts, particularly focusing on the decomposition of vectors and the role of curvature in both surfaces and curves.
Q & A
What is the main focus of video 89 in the series on tensor calculus?
-The main focus of video 89 is to examine how vectors are decomposed into projections and to understand the differences in this process between curves and surfaces in the context of tensor calculus.
What was the initial definition of the covariant derivative discussed in video 68?
-In video 68, the initial definition of the covariant derivative was discussed in the context of a plane, as a simple flat two-dimensional Euclidean manifold, based on the original definition of the Christoffel symbol.
Why can't the initial definition of the covariant derivative be applied to a curved surface?
-The initial definition of the covariant derivative cannot be applied to a curved surface because the partial derivative may result in a vector that points in any direction in space, not necessarily lying in the tangent plane.
What is the role of the Christoffel symbol in the context of a curved surface?
-The Christoffel symbol is used in conjunction with basis vectors to form linear combinations that represent the partial derivative. However, its definition had to be modified for curved surfaces to account for the projection of the partial derivative onto the tangent plane.
What is the significance of the curvature tensor in the modified expression for the covariant derivative on a curved surface?
-The curvature tensor is introduced as a numerical value assigned to the magnitude of the projection of the partial derivative onto the normal, which, when added to the surface projection, gives the correct form for the covariant derivative on a curved surface.
How does the covariant derivative differ when applied to curves compared to surfaces?
-When applied to curves, the covariant derivative must account for the possibility that the partial derivative could result in a vector pointing in any direction in space, unlike on surfaces where the tangent plane provides a clear direction.
What is the vector curvature normal and how is it related to the covariant derivative on a curve?
-The vector curvature normal is a new vector defined to represent the projection of the covariant derivative onto a plane perpendicular to the curve at a point of interest. It is used to account for the additional components of the covariant derivative that are not covered by the tangential projection.
Why is the vector curvature normal orthogonal to the contravariant basis vector along the curve?
-The vector curvature normal is orthogonal to the contravariant basis vector because it is defined as the projection of the covariant derivative onto a plane perpendicular to the curve, ensuring it is perpendicular at the point of interest.
How does the covariant basis vector's non-metronormality relate to the vector curvature normal?
-The covariant basis vector's non-metronormality means that its covariant derivative does not give zero but is equal to the vector curvature normal, indicating a relationship between the basis vector's change and the curvature of the curve.
What is the significance of expressing the vector curvature normal as a linear combination in the context of the covariant derivative on a curve?
-Expressing the vector curvature normal as a linear combination allows for a direct comparison with the analogous expression for curvature on a surface, facilitating a deeper understanding of the curvature properties in both scenarios.
Outlines
📚 Introduction to Vector Decomposition on Curves and Surfaces
This paragraph introduces the topic of vector decomposition, focusing on how vectors are projected differently on curves and surfaces. It reviews the covariant derivative and the role of the Christoffel symbol in flat and curved manifolds. The key takeaway is that the partial derivative may not always lie in the tangent plane, necessitating a modification of the Christoffel symbol to account for the projection onto the tangent plane. This sets the stage for a deeper dive into the decomposition process.
🔍 Analyzing Vector Decomposition on Curves
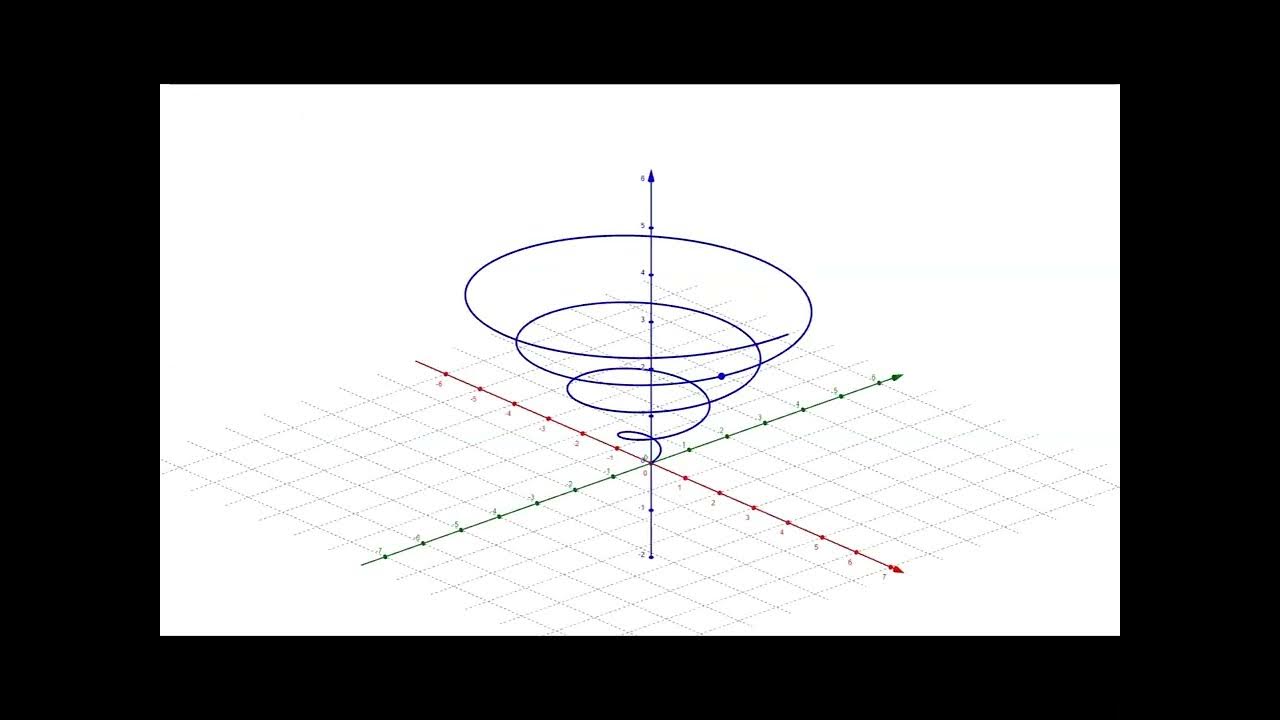
The second paragraph delves into the specifics of vector decomposition on curves. It contrasts the covariant derivative on a curve with that on a surface, highlighting the limitations of the one-dimensional tangent space. The paragraph discusses the need for additional terms to account for the vector components not lying along the tangent. It introduces the concept of a plane perpendicular to the curve at a point of interest, leading to the definition of the vector curvature normal, which is essential for capturing the full three-dimensional behavior of vectors on curves.
📐 Deriving the Vector Curvature Normal
In this paragraph, the focus shifts to deriving the vector curvature normal for curves. It explains the process of taking projections onto the newly defined plane and the significance of the vector curvature normal in describing the general expression for the covariant derivative on a curve. The paragraph also discusses the symmetric properties of the indexes involved and the orthogonal relationship between the vector curvature normal and the contravariant basis vector.
🧩 Exploring the Properties of the Vector Curvature Normal
The fourth paragraph explores the properties of the vector curvature normal in detail. It discusses the orthogonality of the vector to the curve, the non-metronic nature of the covariant basis vector, and the relationship between the vector curvature normal and the Laplacian of the position vector. The paragraph also presents a method to evaluate the vector curvature normal in real terms, using the chain rule and the concept of the derivative with respect to the curve's parameter.
🔗 Relating Curve and Surface Manifold Equations
The final paragraph ties together the concepts discussed throughout the script, drawing parallels between the equations for surface manifolds and those for curves. It emphasizes the role of the principal normal vector in place of the surface normal for curvature calculations on curves. The paragraph concludes by suggesting that by replacing the surface normal with the principal normal, the equations for surfaces can be adapted for curves, setting the stage for further exploration in the next video.
Mindmap
Keywords
💡Covariant Derivative
💡Christophel Symbol
💡Tangent Plane
💡Basis Vectors
💡Normal Component
💡Curvature Tensor
💡Projection
💡Vector Curvature Normal
💡Metronomic
💡Laplacian
💡Principal Normal
Highlights
Introduction to the decomposition of vectors into projections on curves and surfaces in tensor calculus.
Review of the covariant derivative and the role of the Christoffel symbol in flat manifolds.
Exploration of the limitations of the covariant derivative on curved surfaces and the introduction of the normal component.
Diagrammatic explanation of the tangent plane and basis vectors in relation to curved surfaces.
Modified definition of the Christoffel symbol to account for projections onto the tangent plane.
Analysis of the covariant derivative in the context of curves and the need for additional terms.
Introduction of the curvature tensor and its role in the projection of the partial derivative onto the normal.
The process of constructing a plane perpendicular to a curve for the analysis of vector projections.
Definition of the vector curvature normal and its significance in the context of curves.
Dot product analysis to demonstrate the orthogonality of the vector curvature normal to the contravariant basis vector.
Derivation of the covariant derivative of the covariant basis vector and its implications.
Expression of the vector curvature normal in terms of the Laplacian of the position vector.
Evaluation of the vector curvature normal using the chain rule and its relation to the curvature of a line.
Connection between the vector curvature normal and the principal normal of a curve.
Discussion on the analogy between the expressions for curvature on surfaces and curves, emphasizing the use of p-hat instead of n-hat.
Summary of the relationships and expressions involving the vector curvature normal and its practical applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: