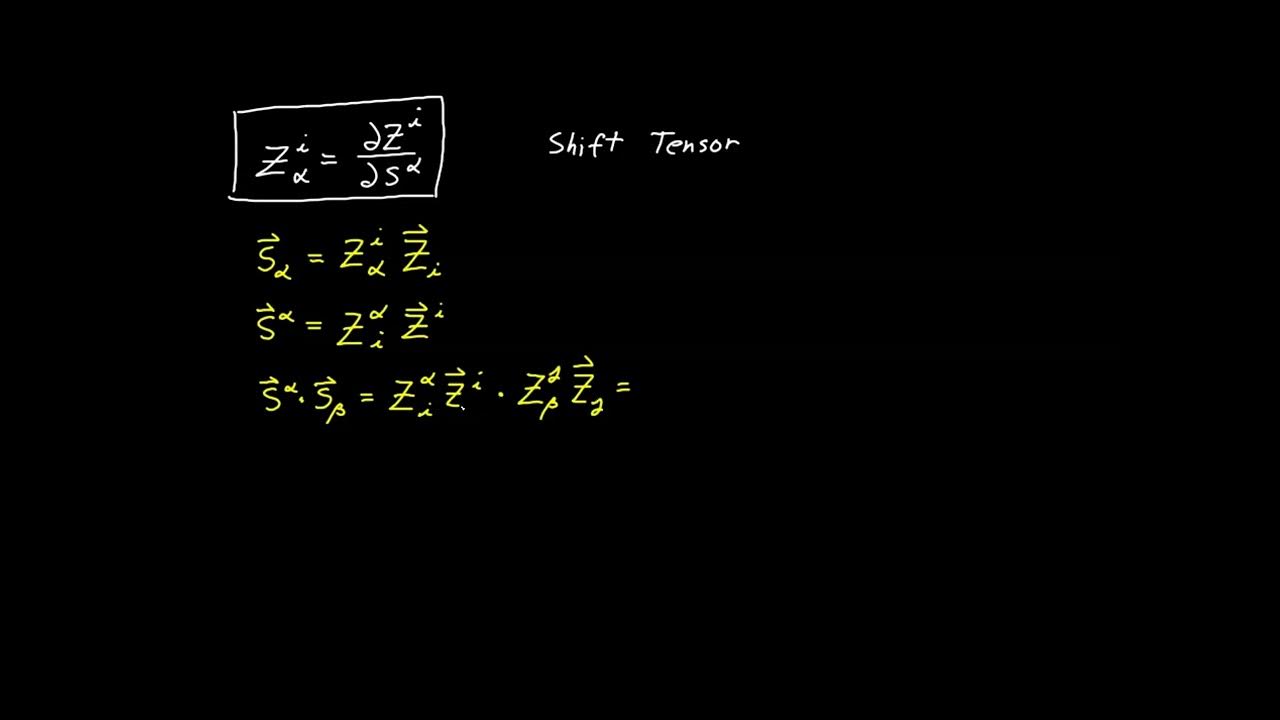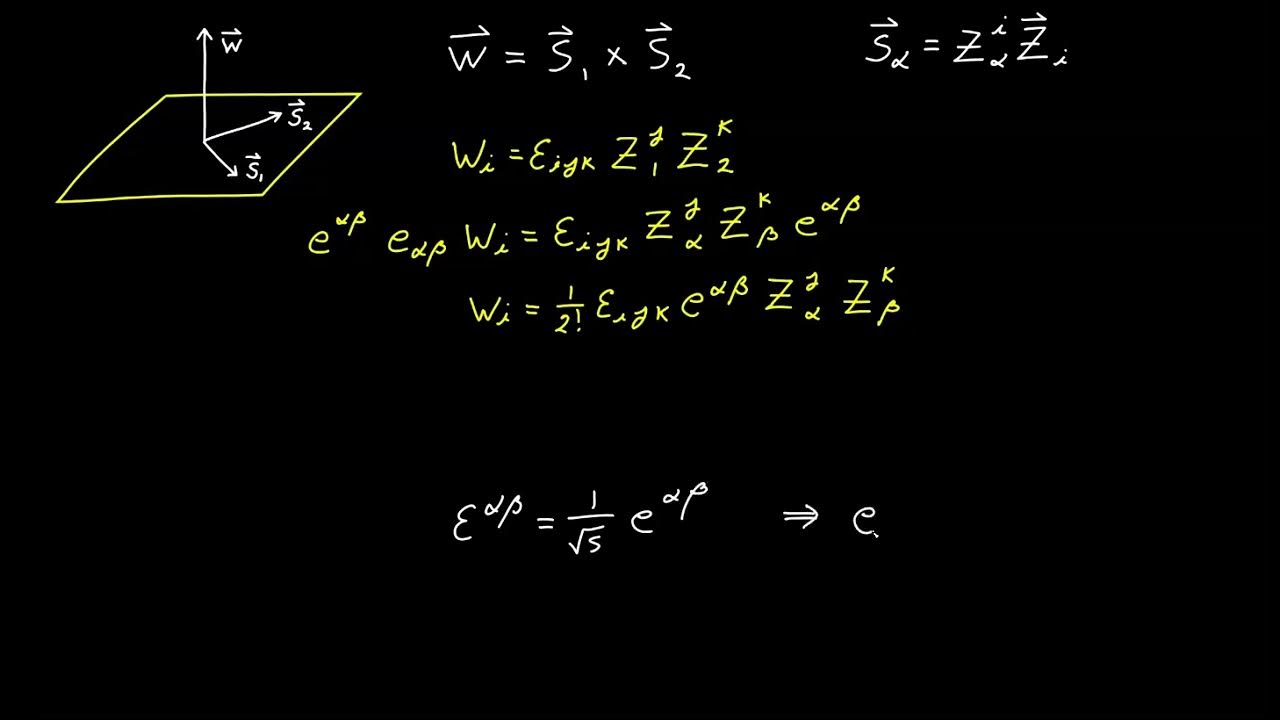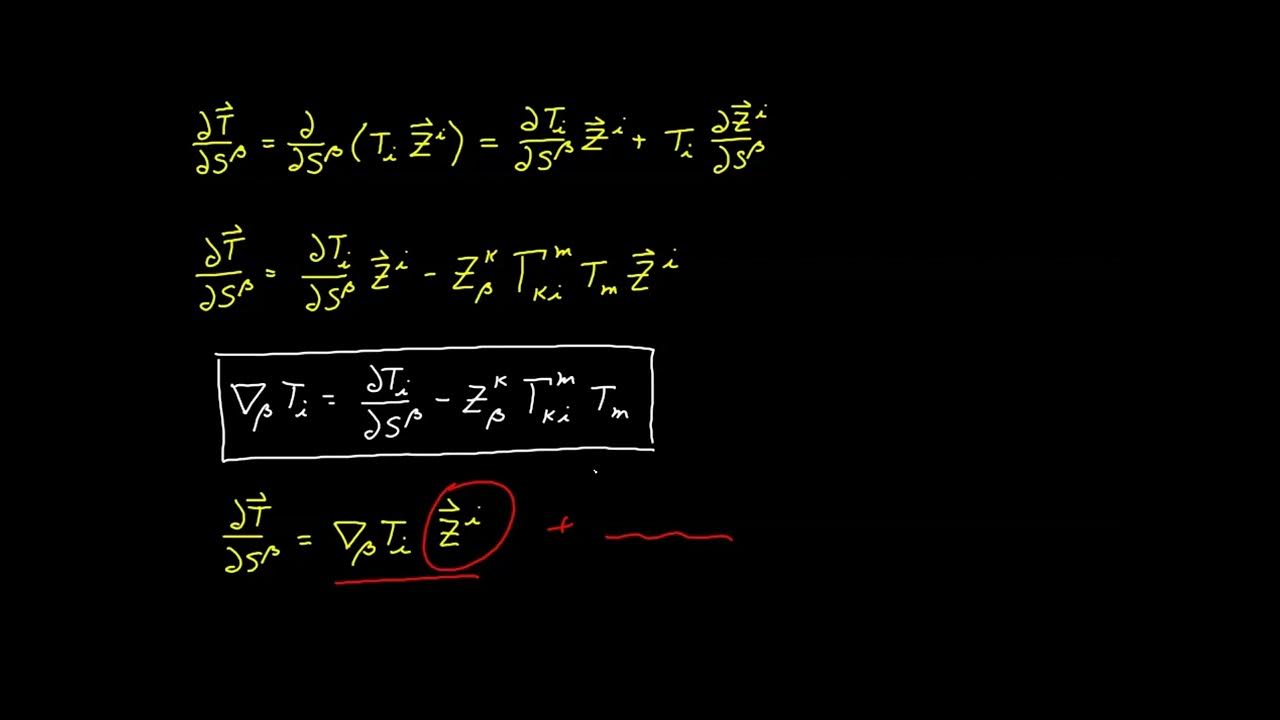Video 65 - Tangent Space Transformations

Tensor Calculus

5 Jun 202222:38

EducationalLearning

32 Likes 10 Comments

TLDRThis video, part of a series on tensor calculus, explores the manipulation of vectors within the tangent space. It explains how to decompose a vector into its surface and normal projections, represented by vectors t and p, respectively. The script delves into transforming these vectors between ambient and tangent spaces using basis vectors and the shift tensor. It concludes by demonstrating how to convert between the two spaces using derived expressions, setting the stage for further discussion on projection operators in upcoming videos.

Takeaways

📚 The video is part of a series on tensor calculus, focusing on working with vectors in tangent space and their transformations between ambient and tangent spaces.
📐 The concept of a tangent space, introduced in a previous video, includes a tangent plane and a normal vector perpendicular to the point of interest.
🔍 The script explains how to decompose a general vector 'v' into its projection components on the tangent plane (vector 't') and away from the surface (vector 'p').
🌟 Vector 't' is the surface projection of 'v', representing the shadow of 'v' when light shines perpendicularly onto the tangent plane.
📍 Vector 'p' is the normal projection of 'v', indicating the component of 'v' that is perpendicular to the tangent plane.
🔄 The script demonstrates the relationship between vector 'v', 't', and 'p', showing that 'v' is the sum of 't' and 'p'.
🧠 The basis vectors 's1' and 's2' represent any vector on the tangent plane, while the normal vector defines the third basis vector in the tangent space.
🔬 The transformation from ambient space to tangent space is achieved by expressing the vector 't' as a linear combination of the surface basis vectors and 'p' as a scalar multiple of the normal basis vector.
⚙️ The video derives expressions for 't alpha' and 'p' as functions of the ambient space vector components 'v i', using the shift tensor and normal vector.
🔄 The reverse transformation from tangent space to ambient space is also discussed, with expressions for 't i' and 'p i' as functions of the tangent space components 't alpha' and 'p'.
🔑 The final expressions allow for the representation of a vector 'v' in terms of the basis vectors of either the ambient or tangent space, depending on the known components.

Q & A

What is the main focus of this video in the series on tensor calculus?
-The main focus of this video is to teach how to work with vectors in the tangent space, specifically how to transform them back and forth between ambient space and tangent space.
What is the significance of the tangent space in the context of this video?
-The tangent space is significant as it is the space where vectors can be decomposed into their projection components, which is essential for understanding transformations between ambient and tangent spaces.
What is the first step in decomposing a vector in the tangent space?
-The first step in decomposing a vector in the tangent space is to drop a perpendicular from the tip of the vector to the tangent plane, creating a projection vector t that lies on the tangent plane.
What is the term used to describe the vector t in the tangent space?
-The vector t is referred to as the projection of vector v onto the surface, also known as the surface projection.
How is the vector t related to the shadow of vector v if a light source is shining from above?
-Vector t is the shadow of vector v on the plane, as it represents the projection of v onto the tangent plane, similar to how a shadow is cast.
What is the normal projection and how is it represented in the video?
-The normal projection is the projection of vector v onto the normal, represented as vector p in the video. It is the component of v that is perpendicular to the tangent plane.
What is the relationship between vector v and the projection vectors t and p?
-The relationship between vector v and the projection vectors t and p is that vector v is equal to the sum of vectors t and p (v = t + p), representing the decomposition of v into its projection components.
What are the basis vectors used to represent any vector that lies on the tangent plane?
-The basis vectors used to represent any vector on the tangent plane are s1 and s2, which are the surface basis vectors, along with the normal vector n-hat.
How can the components of a vector in ambient space be transformed to the tangent space?
-The components of a vector in ambient space can be transformed to the tangent space by finding the relationship between the ambient space components (vi) and the tangent space components (t_alpha and p), using the shift tensor and the normal vector.
What is the process to transform a vector from the tangent space back to the ambient space?
-To transform a vector from the tangent space back to the ambient space, one needs to find the expressions for ti and pi as functions of t_alpha and p, and then substitute these into the formula that represents the vector as a linear combination using the basis vectors in the ambient space.
What is the purpose of introducing projection operators in the next video?
-The purpose of introducing projection operators in the next video is to further elaborate on the concept of transforming vectors between ambient and tangent spaces, providing a more formalized and mathematical approach to the process.

Outlines

00:00

📚 Introduction to Tangent Space and Vector Decomposition

This paragraph introduces the concept of tangent space, revisiting the basis vectors defined in a previous video (Video 58). It explains the process of working with vectors in tangent space, specifically focusing on transforming vectors between ambient and tangent spaces. The paragraph describes the decomposition of a general vector 'v' into its projection components: a surface projection 't' onto the tangent plane and a normal projection 'p' away from the surface. The key takeaway is the understanding that vector 'v' can be represented as the sum of these two projections, 't' and 'p'.

05:01

🔍 Decomposing Vectors Using Basis Vectors

The second paragraph delves into the mathematical representation of the decomposition process. It outlines the use of basis vectors 's1' and 's2' for the tangent plane and a normal vector for the third dimension to express any vector on the tangent plane. The paragraph explains how to express the surface projection 't' and the normal projection 'p' as linear combinations of these basis vectors. The goal is to find relationships that allow the transformation of vector components from ambient space to tangent space, and vice versa, using these basis vectors.

10:01

🔬 Deriving the Relationship Between Ambient and Tangent Space Vectors

This paragraph focuses on the derivation of the relationship between the components of a vector in ambient space ('v_i') and its projections in tangent space ('t_alpha' and 'p'). It uses the dot product and the properties of the shift tensor to establish these relationships. The process involves taking the dot product of the decomposed vector 't' with the contravariant surface basis vector 's_alpha' and simplifying the expression using the orthogonality of 'p' to the tangent plane. The result is an expression for 't_alpha' in terms of 'v_i', which is a crucial step in transforming vectors from ambient to tangent space.

15:04

📐 Geometric Interpretation of Vector Projection

The fourth paragraph provides a geometric interpretation of the normal projection 'p'. It explains that 'p' can be found using the right triangle formed by the vector 'v' and the normal to the tangent plane. The magnitude of 'p' is derived as the magnitude of 'v' multiplied by the cosine of the angle between 'v' and the normal vector. The paragraph then translates this geometric relationship into an algebraic one using the dot product, leading to an expression for 'p' in terms of 'v_i' by substituting the cosine of the angle with the relevant dot product terms.

20:05

🔄 Transformation Between Ambient and Tangent Spaces

The final paragraph summarizes the process of transforming vectors from ambient space to tangent space and back. It provides the formulas for these transformations, which involve substituting the derived expressions for 't_alpha' and 'p' back into the linear combinations of basis vectors. The paragraph clarifies the distinction between the scalar value 'p' and its vector components 'p_i' in ambient space. It concludes by reiterating the method for representing a vector 'v' in terms of the basis vectors in both spaces, emphasizing the utility of these transformations in understanding and working with vectors in differential geometry.

Mindmap

Keywords

💡Tensor

A tensor is a mathematical object that generalizes scalars, vectors, and matrices to handle multi-dimensional data. In the context of the video, tensors are used to describe the properties of space, particularly in the study of manifolds and their tangent spaces. The script discusses the manipulation of tensors to understand and work with vectors in a tangent space.

💡Tangent Space

The tangent space is a concept in differential geometry where it is defined as a vector space that is tangent to a manifold at a given point. In the video, the tangent space is introduced as a critical structure that includes a tangent plane and a normal vector, which are used to decompose and understand vectors in the vicinity of a point on a manifold.

💡Basis Vectors

Basis vectors are the fundamental vectors in a vector space that can be combined through scalar multiplication to form any vector in that space. The script mentions basis vectors s1 and s2 that define the tangent plane, and a normal basis vector that defines the direction perpendicular to the tangent plane, essential for understanding the transformations between ambient and tangent spaces.

💡Projection

Projection in the video refers to the process of mapping a vector onto a subspace, resulting in a new vector that lies within that subspace. There are two types discussed: the surface projection (vector t) which lies on the tangent plane, and the normal projection (vector p) which is perpendicular to the tangent plane. These projections are key to decomposing a vector into components that can be analyzed within the tangent space.

💡Ambient Space

Ambient space is the larger space in which a manifold is embedded. In the video, the concept of ambient space is used to contrast with the tangent space, where vectors are initially defined and then transformed into the tangent space for analysis. The script discusses the process of transforming vectors from ambient to tangent space and vice versa.

💡Decomposition

Decomposition in this context refers to the breakdown of a vector into its components along different basis vectors. The script explains how a general vector v can be decomposed into its projection on the tangent plane (vector t) and its projection away from the surface (vector p), which together make up the original vector v.

💡Shift Tensor

The shift tensor is a tool used in differential geometry to transform between covariant and contravariant vector components. In the script, it is used to express the relationship between the components of a vector in ambient space and its representation in the tangent space, facilitating the transformation process.

💡Covariant Basis Vectors

Covariant basis vectors are used to express vectors in a coordinate system where the basis vectors change with the coordinates. In the video, the script describes how vector t can be represented as a linear combination of covariant basis vectors s1 and s2, which lie on the tangent plane.

💡Contravariant Basis Vectors

Contravariant basis vectors are dual to covariant basis vectors and are used in the context of dual spaces. The script mentions the use of contravariant basis vectors to express the normal vector n-hat, which is perpendicular to the tangent plane and part of the basis for the tangent space.

💡Transformation

Transformation in the video refers to the mathematical process of converting vector components from one coordinate system to another. The script details the formulas for transforming vectors from ambient space, where they are initially defined, to the tangent space, and the reverse process, which involves understanding the relationships between the components in both spaces.

💡Projection Operators

Projection operators are mathematical tools used to project vectors onto subspaces. Although not deeply discussed in the provided script, they are mentioned as the next topic in the series. Projection operators would be essential for further analysis of vectors within the tangent space and their decomposition.

Highlights

Introduction to working with vectors in tangent space and transforming them between ambient and tangent space.

Explanation of the concept of a tangent space, including a tangent plane and a normal.

Decomposition of a general vector 'v' into its projection components.

Construction of a vector 't' as the projection of vector 'v' onto the tangent plane.

Vector 't' described as the shadow of vector 'v' on the plane, illustrating the projection concept.

Introduction of vector 'p' as the normal projection of 'v' away from the surface.

The relationship that vector 'v' equals the sum of vectors 't' and 'p'.

Use of basis vectors 's1' and 's2' to represent any vector on the tangent plane.

Expression of vector 't' as a linear combination of surface basis vectors.

Vector 'p' expressed as a scalar value times the normal basis vector.

Derivation of the relationship between vector components 'vi' in ambient space and 't alpha'.

Finding the value of 'p' as a function of 'vi' using geometric concepts and the dot product.

Transformation from ambient space to tangent space using the derived expressions.

Transformation from tangent space to ambient space and the reverse process.

Final expressions for transforming vector 'v' between ambient and tangent spaces.

Recap of the process and the significance of the projection operators in tensor calculus.

Transcripts

Browse More Related Video

Video 60 - Shift Tensor

Video 63 - The Normal

Video 58 - Tangent Space

Video 91 - Frenet Formulas

Tensor Calculus For Physics Majors 002 | Vector Transformations and Vectors as Matrices

Video 72 - Surface Covariant Derivative for Non Tangent Vectors

Related Tags

Vector Decomposition Tangent Space Ambient Space Calculus Concepts Basis Vectors Surface Projection Normal Projection Tensor Analysis Geometry Tutorial Mathematics Education