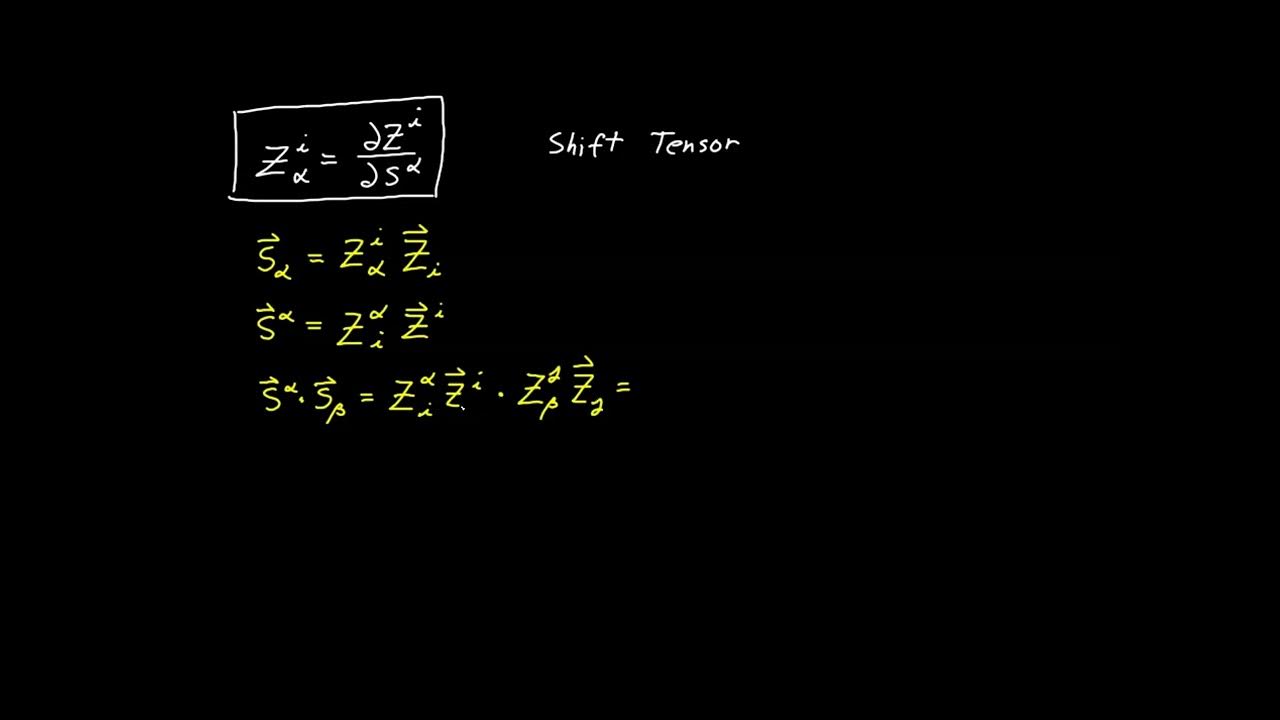Tensor Calculus 2: Cartesian/Polar Coordinates, and Basis Vectors
TLDRThis video script explores Cartesian and polar coordinates in two-dimensional space, explaining their applications and the rationale behind using different coordinate systems. It delves into converting points between these systems, utilizing trigonometric relationships and Pythagoras' theorem. The script further introduces basis vectors in both coordinate systems, illustrating their directional significance and connection to partial derivatives. The unique behaviors of polar basis vectors, changing both direction and magnitude, are highlighted, offering insights into tensor calculus and setting the stage for future discussions on coordinate transformations.
Takeaways
- 📐 The video discusses Cartesian and polar coordinates in two dimensions, explaining how they are used to measure geometrical objects on a flat plane.
- 🌐 Cartesian coordinates use x and y to denote horizontal and vertical positions relative to an origin point, while polar coordinates use r and theta for radius and angle from a horizontal axis.
- 🔍 The need for multiple coordinate systems arises because certain problems are more easily solved in specific systems, such as motion in Cartesian and circular paths in polar coordinates.
- 🤔 The independence of physical laws from human-invented coordinate systems is emphasized, highlighting the importance of verifying that physical laws hold true across different systems.
- 🔄 The script explains the conversion process between Cartesian (x, y) and polar (r, theta) coordinates, using basic trigonometric relationships.
- 📉 Pythagoras's theorem is used to derive the relationship between Cartesian coordinates and the radius in polar coordinates (R = sqrt(x^2 + y^2)).
- 📈 The inverse tangent function is key to converting from Cartesian to polar coordinates to find the angle theta (theta = arctan(y/x)).
- 📍 Basis vectors in both coordinate systems are introduced, showing how they are derived from the directions of coordinate lines or curves in the space.
- 🧭 A novel interpretation of basis vectors is presented, where they are seen as equivalent to partial derivatives of a position vector along coordinate curves.
- 🌀 The e_r basis vector in polar coordinates is unique as it changes direction and length across the plane, unlike Cartesian basis vectors which are constant.
- 📚 The script mentions that textbooks might normalize the e_theta vector to have a length of 1, which differs from the approach taken in the video.
Q & A
What is the purpose of using coordinate systems in geometry?
-Coordinate systems are used to quantify and calculate geometrical objects such as distances between points or lengths of curves, making it easier to analyze and describe these objects numerically.
What are the two most common coordinate systems for a two-dimensional plane?
-The two most common coordinate systems for a two-dimensional plane are the Cartesian coordinate system and the polar coordinate system.
How are points represented in the Cartesian coordinate system?
-In the Cartesian coordinate system, points are represented by coordinates x and y, which measure the horizontal and vertical positions of a point relative to a special origin point.
What are the coordinates used in the polar coordinate system?
-In the polar coordinate system, points are represented by lowercase r (radius) and theta (angle), which measure the radius from the origin and the angle of counterclockwise rotation from a horizontal axis, respectively.
Why are multiple coordinate systems useful?
-Multiple coordinate systems are useful because some problems are easier to solve in certain coordinate systems due to their alignment with the motion or shape being studied, and to ensure that the laws of physics are independent of any human-invented coordinate system.
How can you convert from polar coordinates (r, theta) to Cartesian coordinates (x, y)?
-To convert from polar to Cartesian coordinates, you can use the formulas x = r * cos(theta) and y = r * sin(theta), where r is the radius and theta is the angle in the polar coordinate system.
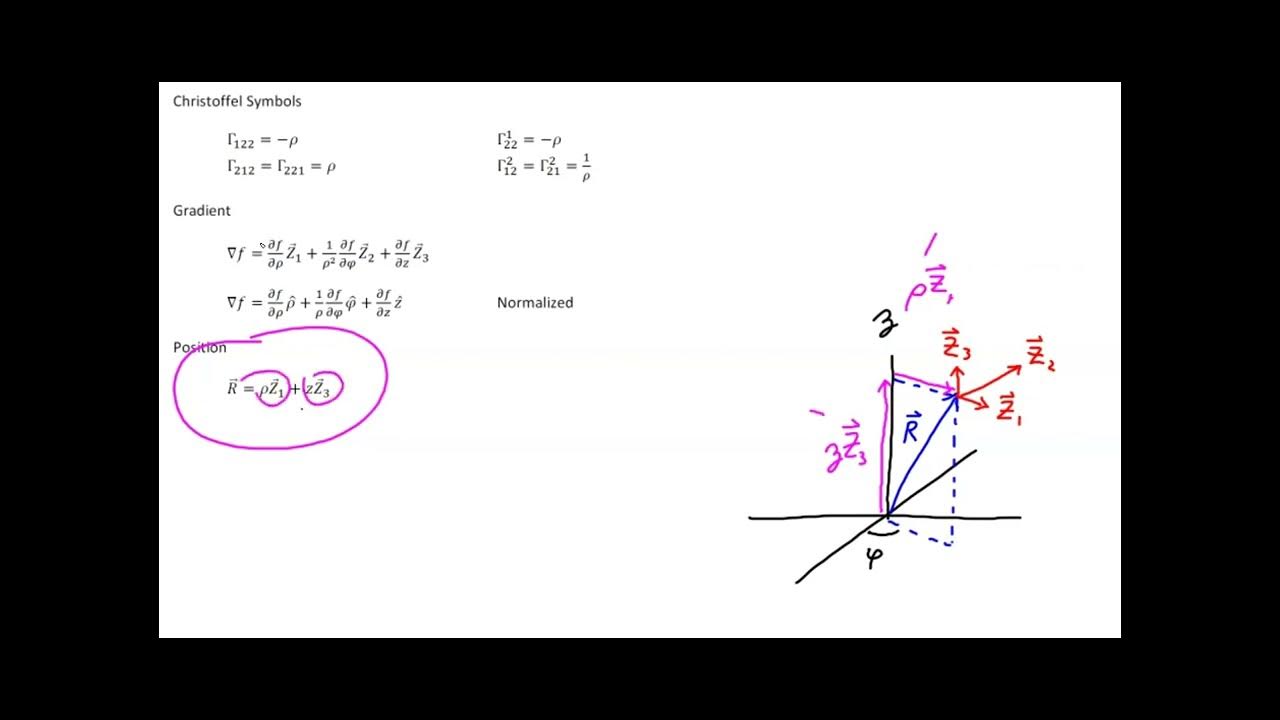
What is the relationship between the basis vectors in Cartesian and polar coordinate systems?
-In Cartesian coordinates, the basis vectors are constant (e_x and e_y), while in polar coordinates, the basis vectors (e_r and e_theta) change direction and length from point to point, depending on the position in the 2D plane.
How can basis vectors be derived from partial derivatives in tensor calculus?
-Basis vectors can be derived from partial derivatives by considering the limit of a position vector as it moves infinitesimally along the coordinate axes or curves, resulting in unit vectors in the direction of those axes or curves.
Why might the use of partial derivatives as basis vectors seem strange at first?
-The use of partial derivatives as basis vectors might seem strange because it is a different conceptual approach from the traditional understanding of vectors as fixed direction arrows, but it is actually a powerful method for understanding transformations between coordinate systems.
What is the significance of the forward and backward transformations between coordinate systems?
-The forward and backward transformations between coordinate systems are significant because they allow for the conversion of coordinates from one system to another, which is essential for solving problems in different contexts and understanding the underlying physics.
How does the e_theta basis vector behave in polar coordinates?
-The e_theta basis vector in polar coordinates changes both direction and length as you move away from the origin. A small change in the theta coordinate results in a larger change in the position vector as the radius increases.
Outlines
📐 Introduction to Cartesian and Polar Coordinates
This paragraph introduces the concept of Cartesian and polar coordinates in two-dimensional space. It explains how coordinate systems are used to quantify geometrical objects and facilitate calculations such as distances and lengths. The Cartesian system uses x and y coordinates relative to an origin point, while the polar system uses radius (R) and angle (theta). The paragraph also discusses the reasons for using different coordinate systems, emphasizing their utility in solving specific problems and the importance of ensuring physical laws are independent of the coordinate system chosen.
🔍 Conversion Between Cartesian and Polar Coordinates
This section delves into the process of converting between Cartesian (X, Y) and polar (R, theta) coordinates. It describes the method of determining the coordinates of a point P in both systems using a triangle formed with the origin. The relationships between X, Y, R, and theta are explained using trigonometric functions, with X = R * cos(theta) and Y = R * sin(theta) for converting from polar to Cartesian, and R = sqrt(X^2 + Y^2) and theta = arctan(Y/X) for the reverse conversion. The paragraph also introduces the concept of basis vectors in both coordinate systems, illustrating how they are derived from the grid lines of the coordinate systems.
🌐 Basis Vectors and Their Interpretation in Tensor Calculus
The final paragraph explores the concept of basis vectors in Cartesian and polar coordinates, explaining how they can be determined by following the directions of the coordinate lines. It introduces a novel interpretation of basis vectors as partial derivatives of a position vector along the coordinate curves. This interpretation is demonstrated for both Cartesian coordinates, where basis vectors e_x and e_y are constant, and polar coordinates, where the basis vectors e_r and e_theta change direction and length depending on the point in the plane. The paragraph also touches on the common textbook approach to normalize the e_theta vector by dividing by R, but it questions the naturalness of this choice.
Mindmap
Keywords
💡Cartesian coordinates
💡Polar coordinates
💡Coordinate systems
💡Basis vectors
💡Partial derivatives
💡Conversion formulas
💡Pythagorean theorem
💡Tangent function
💡Trigonometric functions
💡Multivariable chain rule
Highlights
Introduction to Cartesian and polar coordinates in two-dimensional space.
Explanation of the physical existence of geometrical objects independent of any coordinate system.
The role of coordinate systems in facilitating calculations like distance between points or length of curves.
Differentiation between Cartesian coordinates using x and y, and polar coordinates using r and theta.
Reasons for inventing multiple coordinate systems: problem-solving ease and independence from human constructs.
Illustration of converting between Cartesian and polar coordinates using geometrical relationships.
Conversion formulas from polar to Cartesian coordinates using cosine and sine functions.
Conversion from Cartesian to polar coordinates using Pythagoras's theorem and the arctan function.
Definition of basis vectors in Cartesian and polar coordinates through grid lines and coordinate curves.
Interpretation of basis vectors as the result of following the directions of coordinate lines.
Introduction of a new perspective on basis vectors as partial derivatives of position vectors.
Demonstration of how partial derivatives equate to basis vectors in Cartesian coordinates.
Explanation of how the ER basis vector in polar coordinates changes direction and length.
Discussion on the e_theta basis vector's variability in both direction and magnitude with radial distance.
Difference in the treatment of the e_theta vector between the video and traditional textbooks.
Summary of the video's content on converting point coordinates and the new interpretation of basis vectors.
Teaser for the next video on forward and backward transformations between coordinate systems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: