But what is the Fourier Transform? A visual introduction.

This paragraph introduces the concept of the Fourier transform, a mathematical technique used to decompose signals into their constituent frequencies. It emphasizes the goal of providing an animated visual approach to understanding this fundamental idea from mathematics. The example of decomposing sound frequencies is used to illustrate the concept, highlighting the ubiquity of the Fourier transform across various fields such as math and physics. The paragraph sets the stage for a deeper exploration of how the Fourier transform can reveal the hidden frequencies within a complex signal.

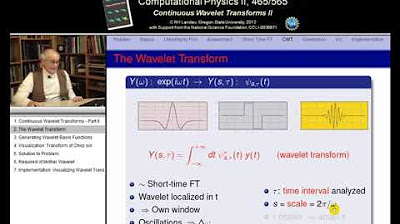
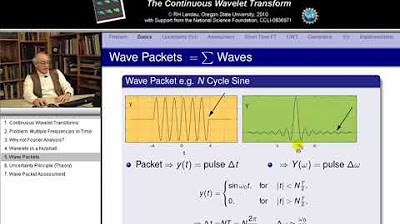
The paragraph delves into the specifics of how sound frequencies can be visualized using the Fourier transform. It explains the process of taking a pure frequency signal and wrapping it around a circle, with the length of a rotating vector representing the signal's intensity at different times. The discussion focuses on the center of mass of the wrapped graph and how it shifts with different winding frequencies. The key insight is that when the winding frequency matches the signal's frequency, the center of mass moves far to the right, indicating a peak in the signal. This visual representation forms the basis for the 'almost Fourier transform,' which is used to identify the frequencies present in a mixed signal.

This section builds on the previous discussion by exploring the process of unmixing multiple frequencies in a signal. It describes how the almost Fourier transform can be used to identify individual frequencies within a complex waveform. The concept is illustrated by adding two pure frequency signals and showing how the winding frequency machine can reveal the original frequencies at 2 and 3 beats per second. The paragraph also touches on the property of the Fourier transform that allows for the addition of individual transforms to be equivalent to the transform of the summed signal, highlighting the practical applications of this mathematical tool in fields like sound editing.

The paragraph introduces the use of complex numbers in the Fourier transform process. It explains that the center of mass of the wrapped graph is represented as a complex number with both real and imaginary parts. The concept of Euler's formula is introduced to describe rotation in the complex plane. The paragraph then presents a formula for winding up the graph, which involves an integral of a complex-valued function, representing the center of mass of the graph. The distinction between this 'winding machine' and the actual Fourier transform is clarified by noting that the latter does not divide by the time interval, effectively scaling up the center of mass by the duration of the signal.

The final paragraph discusses the practical applications of the Fourier transform, particularly in sound editing, and touches on the concept of the inverse Fourier transform. It also hints at the broader implications of the Fourier transform in mathematics and physics. The video concludes with a mathematical puzzle from the sponsor, Jane Street, which serves as a teaser for future content and a call to action for viewers interested in mathematical problem-solving and career opportunities in quantitative trading.

This paragraph provides information about career opportunities at Jane Street, a quantitative trading firm that values intellectual curiosity and problem-solving skills. It mentions that the company is looking for both full-time employees and interns, and emphasizes that a background in finance is less important than one's ability to think critically and solve complex problems. The paragraph concludes with a call to action for viewers to learn more about Jane Street and apply for open positions.