Learn Standard Deviation - Formula & Examples | Step-by-Step

Math and Science
29 Mar 202312:39
EducationalLearning
32 Likes 10 Comments

TLDRThis script delves into the concept of standard deviation, a fundamental statistical measure that quantifies the spread of data. It clarifies the difference between variance and standard deviation, emphasizing the latter's practicality in real-world data description. The explanation simplifies the calculation of standard deviation as the square root of variance, illustrating how it reflects the data's dispersion in the original unit of measurement. The script uses relatable examples, such as classroom grades and ages, to demonstrate how mean and standard deviation together provide a comprehensive understanding of a dataset's distribution.

Takeaways
  • πŸ“š Standard deviation is a common term used to measure the spread of data in statistics.
  • πŸ”’ The mean and standard deviation are often mentioned together to describe a dataset, with the mean representing the average value and the standard deviation indicating the dispersion.
  • πŸ“‰ Variance is a related concept to standard deviation but represents the spread in squared units, making it less intuitive to interpret directly.
  • 🌐 The sample variance (s^2) is calculated as the sum of the squared differences from the mean, divided by n-1, where n is the sample size.
  • 🌍 The population variance (Ξ£^2) is similar but uses the total number of data points in the population and divides by the population size.
  • πŸ›  To make variance more interpretable, the standard deviation is derived by taking the square root of the variance, thus returning to the original unit of measurement.
  • πŸ“Š The sample standard deviation (s) is the square root of the sample variance, and it helps in understanding the spread of the data in its original units.
  • 🌐 The population standard deviation (Οƒ) is calculated in the same way as the sample standard deviation but using the population variance.
  • πŸ“ˆ Understanding standard deviation is crucial for interpreting data, as it provides insight into the data's dispersion around the mean.
  • πŸ“š The script emphasizes the importance of standard deviation in statistics, as it is a fundamental concept for describing and comparing datasets.
  • πŸ“ The script suggests that practice is essential for mastering the calculation of standard deviation and understanding its significance in data analysis.
Q & A

  • What is standard deviation?

    -Standard deviation is a measure of the amount of variation or dispersion in a set of values. It helps to understand how spread out the data is from the mean or average value.

  • Why is standard deviation more commonly used than variance when describing data sets?

    -Standard deviation is more commonly used than variance because it is in the same units as the original data, making it easier to interpret and describe the spread of the data without the need to square the differences.

  • What is the formula for calculating sample variance?

    -The formula for calculating sample variance (denoted as sΒ²) is the sum of the squared differences between each data point and the sample mean, divided by (n - 1), where n is the number of data points.

  • What is the difference between sample variance and population variance?

    -Sample variance is calculated using the formula for variance with (n - 1) in the denominator, while population variance uses the total number of items in the population (n) as the denominator.

  • How is sample standard deviation calculated?

    -Sample standard deviation (denoted as s) is calculated by taking the square root of the sample variance. This eliminates the squaring of differences and returns the measure in the original units of the data.

  • What does a standard deviation of 10 points in a classroom grade mean?

    -A standard deviation of 10 points in a classroom grade means that, on average, most of the grades fall within 10 points above or below the mean grade. If the mean is 80, then many grades are expected to be between 70 and 90.

  • How does the standard deviation relate to the mean of a data set?

    -The standard deviation provides information about the spread of the data around the mean. A larger standard deviation indicates a more spread out data set, while a smaller standard deviation indicates a more tightly packed data set around the mean.

  • What is the formula for calculating population standard deviation?

    -Population standard deviation (denoted as Οƒ) is calculated by taking the square root of the population variance, which is the sum of the squared differences between each data point and the population mean, divided by the total number of items in the population.

  • Why is it important to understand both variance and standard deviation?

    -Understanding both variance and standard deviation is important because while variance gives the magnitude of the spread without units, standard deviation provides a more intuitive measure of spread in the same units as the data, making it easier to communicate and interpret.

  • Can you provide an example of how standard deviation can be used to describe a data set?

    -Sure, if you have a classroom where the mean age is 15 years and the standard deviation is 10 years, it means that most students' ages fall within 5 to 25 years (15 Β± 10), giving you an idea of the age range and spread of the students.

  • What does a large standard deviation relative to the mean indicate about a data set?

    -A large standard deviation relative to the mean indicates that the data points are spread out over a wider range, with many values lying far from the mean. It suggests greater variability within the data set.

Outlines
00:00
πŸ“š Understanding Standard Deviation

This paragraph introduces the concept of standard deviation as a measure of data spread, often discussed in educational settings. It explains the difference between sample variance (s^2) and population variance (Ξ£^2), emphasizing their role in quantifying dispersion but pointing out the limitation that variance is in squared units, making it less intuitive. The speaker clarifies that standard deviation rectifies this by taking the square root of variance, thus maintaining the original data's unit of measure. The formula for sample standard deviation is outlined, highlighting the process of squaring differences from the mean, averaging, and then taking the square root.

05:02
πŸ“‰ Standard Deviation vs. Variance

The speaker elaborates on the practicality of standard deviation over variance for describing data sets. By using the classroom grades example, they illustrate how standard deviation in points directly relates to the data, unlike variance which is in squared units. The paragraph also introduces the concept of population standard deviation, calculated similarly to the sample version but using the entire data set. The importance of both sample and population standard deviations in statistics is stressed, as they provide a clear and intuitive measure of data spread.

10:03
πŸ“ˆ Visualizing Data with Mean and Standard Deviation

This paragraph uses the example of ages in a classroom to demonstrate how the mean and standard deviation can be used to visualize and understand a data set. The mean represents the central value, while the standard deviation indicates the spread around this mean. By adjusting the standard deviation value, the speaker shows how it affects the perceived spread of the data, with a larger standard deviation indicating a broader range of values and a smaller one suggesting a more concentrated set of data points.

Mindmap
Keywords
πŸ’‘Standard Deviation
Standard deviation is a measure of the amount of variation or dispersion in a set of values. It indicates the average distance of each data point from the mean. In the video, standard deviation is explained as a crucial concept for understanding the spread of data, with the script providing the formula for calculating it and emphasizing its importance over variance due to its use in the same units as the data set.
πŸ’‘Mean
The mean, often referred to as the average, is the sum of all data points divided by the number of points. It serves as a central value in a data set. The video uses the mean to establish a reference point from which the spread of data is measured, such as stating that if the mean grade in a class is 80, it provides a starting point to discuss how grades vary using standard deviation.
πŸ’‘Variance
Variance is a statistical measure that represents the average of the squared differences from the Mean. It quantifies the dispersion of a set of data points. The script explains variance as a precursor to understanding standard deviation, noting that while it measures spread, it does so in squared units, which can be less intuitive than standard deviation.
πŸ’‘Spread
In statistics, spread refers to the dispersion or distribution of data points around the mean. The video script frequently mentions spread to describe the purpose of standard deviation and variance, emphasizing how these measures help in understanding the distribution of data, such as grades in a classroom.
πŸ’‘Sample Variance
Sample variance is an estimate of the population variance calculated from a sample of data. It is denoted as 's squared' in the script and is calculated by summing the squared differences between each data point and the sample mean, then dividing by the number of observations minus one. The video discusses sample variance as part of the process to calculate the sample standard deviation.
πŸ’‘Population Variance
Population variance, denoted as Sigma squared in the script, is the measure of the dispersion of an entire population's data points. It is calculated similarly to sample variance but includes all data points and divides by the total number of items in the population. The script contrasts this with sample variance to illustrate the difference between estimating from a sample versus the entire population.
πŸ’‘Sample Standard Deviation
Sample standard deviation, represented by 's' in the script, is the square root of the sample variance. It is a measure of the dispersion of a sample set of data points and is used to estimate the population standard deviation. The video explains that it is calculated by taking the square root of the sample variance to revert the squaring process and make it more interpretable.
πŸ’‘Population Standard Deviation
Population standard deviation, represented by the Greek letter Sigma in the script, is the square root of the population variance. It is a measure of the dispersion of the entire population's data points. The script explains that it is calculated in the same way as the sample standard deviation but starts from the population variance.
πŸ’‘Units
Units in the context of the video refer to the measurement scale of the data set, such as points for grades or years for age. The script emphasizes that the standard deviation, unlike variance, is expressed in the same units as the original data, making it easier to interpret and communicate the spread of the data.
πŸ’‘Data Set
A data set is a collection of data points that is used for analysis. The video script uses the term to describe the grades in a classroom or the ages of people in a room, emphasizing the importance of understanding the mean and standard deviation to get an idea of what the data set looks like and how it is distributed.
Highlights

Standard deviation is a commonly used measure to describe the spread of data sets.

Standard deviation is more common than variance in describing data.

The purpose of standard deviation is to measure the spread of data.

Variance measures spread but is in squared units, unlike standard deviation.

Sample variance is calculated as the sum of squared differences from the mean, divided by n-1.

Population variance is similar to sample variance but divided by the total number of items.

Standard deviation corrects the unit issue of variance by taking the square root.

Sample standard deviation is the square root of the sample variance.

Population standard deviation is the square root of the population variance.

Standard deviation provides a more intuitive measure of data spread compared to variance.

Understanding standard deviation helps in visualizing data distribution around the mean.

A large standard deviation indicates a broad spread of data around the mean.

A small standard deviation indicates a tightly packed data set.

The mean and standard deviation together give a clear picture of a data set's characteristics.

The standard deviation calculation will be practiced in the next lesson.

The importance of understanding standard deviation for future statistical lessons is emphasized.

Transcripts

Browse More Related Video

Range, variance and standard deviation as measures of dispersion | Khan Academy

Statistics: Standard deviation | Descriptive statistics | Probability and Statistics | Khan Academy

Measures of Dispersion (Ungrouped Data) | Basic Statistics

Standard Deviation & Mean Absolute Deviation Explained - 6-8-19]

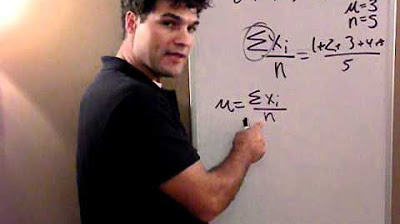
What is a "Standard Deviation?" and where does that formula come from

Standard Deviation and Variance

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Standard DeviationData AnalysisStatistical ConceptsMean CalculationVariance ExplainedEducational ContentMathematics LessonScience EducationSpread MeasurementStatistical Tools