Gas Law Problems Combined & Ideal - Density, Molar Mass, Mole Fraction, Partial Pressure, Effusion

This paragraph introduces the topic of gas laws, emphasizing the importance of understanding how to solve problems related to the ideal gas law and combined gas law. It mentions various laws such as Boyle's, Charles's, Avogadro's, and Graham's law of diffusion, and highlights concepts like gas density, molar mass, partial pressure, and mole fraction. The explanation begins with the definition of pressure and its units, such as Pascal and ATM, and explains the relationship between the number of gas molecule collisions and the pressure exerted.

The second paragraph delves into the ideal gas law equation (PV=nRT), discussing how pressure, volume, moles of gas, and temperature are interrelated. It explains the isothermal condition where temperature is constant and how it leads to Boyle's Law (P1V1=P2V2), indicating the inverse relationship between pressure and volume. The paragraph also covers the combined gas law, which allows for the calculation of gas properties under varying conditions of pressure, volume, and temperature, and introduces Charles's Law (V1/T1=V2/T2) and Avogadro's Law (V1/N1=V2/N2) as specific cases of the combined gas law.

This section focuses on Gay-Lussac's Law, which describes the direct relationship between the pressure of a gas and its temperature, assuming constant volume and moles of gas. It explains that as temperature increases, the kinetic energy of gas molecules also increases, leading to more frequent collisions and thus higher pressure. The paragraph uses the example of heating a pot of water to illustrate the point and emphasizes the linear relationship between temperature and pressure.

The fourth paragraph discusses Charles's Law, which shows the direct relationship between the volume of a gas and its temperature when pressure and the number of moles are held constant. It explains that increasing the temperature of a gas in an expandable container will lead to an increase in volume. The molecular explanation involves gas particles moving faster at higher temperatures, causing the gas to expand against the external pressure until equilibrium is reached.

This paragraph explores Avogadro's Law, which states that the volume of a gas is directly proportional to the number of moles of gas, provided that pressure and temperature are constant. It uses the example of blowing air into a balloon to illustrate how increasing the moles of gas increases the volume. The relationship is linear, and the concept is fundamental for understanding how gas particles occupy space.

The sixth paragraph introduces Dalton's Law of Partial Pressure, which states that the total pressure of a gas mixture is equal to the sum of the partial pressures of the individual gases in the mixture. It explains the concept of mole fractions and how they are used to calculate the partial pressure of each gas in the mixture. The mole fraction is the ratio of the moles of a particular gas to the total moles of all gases present.

The seventh paragraph focuses on the ideal gas law equation (PV=nRT) and its application in calculating various properties of a gas, such as pressure, volume, and the number of moles, given the other variables. It provides a step-by-step approach to solving for pressure when other parameters like volume, moles, and temperature are known, and also discusses how to calculate the mass of a gas using molar mass.

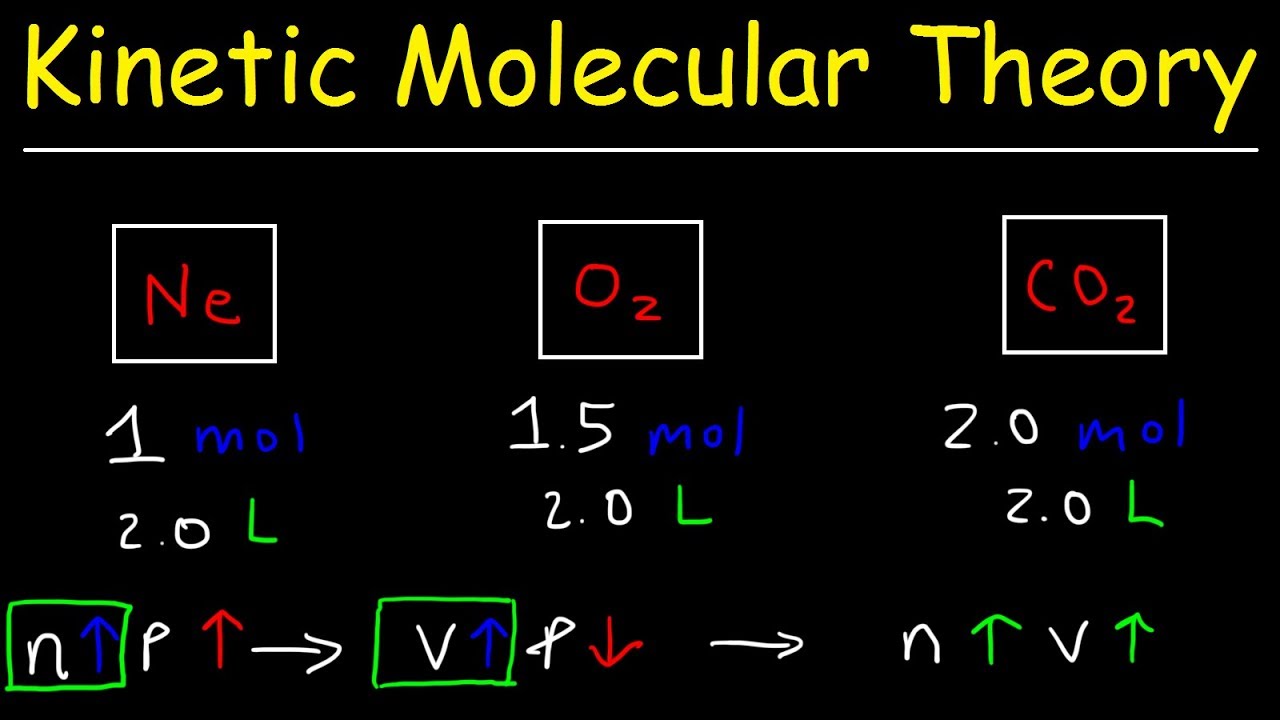
The final paragraph outlines the Kinetic Molecular Theory, which describes the behavior of ideal gases. It highlights that gas molecules are assumed to have negligible volume, move in continuous random motion, and experience perfectly elastic collisions. The theory also assumes that intermolecular forces are negligible. The paragraph differentiates between polar and non-polar gases, noting that non-polar gases like helium behave more ideally due to weaker intermolecular forces. It concludes with the conditions under which a real gas will behave more like an ideal gas, which is at high temperatures and low pressures.