How to calculate wave speed, wavelength, and frequency.

Dustin MAY
15 Oct 202011:23
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains how to calculate the speed of a wave using its frequency and wavelength. It introduces key concepts like speed (or velocity), wavelength, and frequency, including their units and symbols. The formula for wave speed is given as v = λf, where v is speed, λ is wavelength, and f is frequency. The instructor then demonstrates solving for each variable through examples, providing step-by-step calculations for wave speed, wavelength, and frequency. This tutorial is designed to help students understand and apply these basic algebraic equations in physics.

Takeaways
  • 📏 Speed is how fast a wave is traveling, measured in meters per second (m/s).
  • 🔤 The symbol for speed can be 'v' for velocity or 's' for speed.
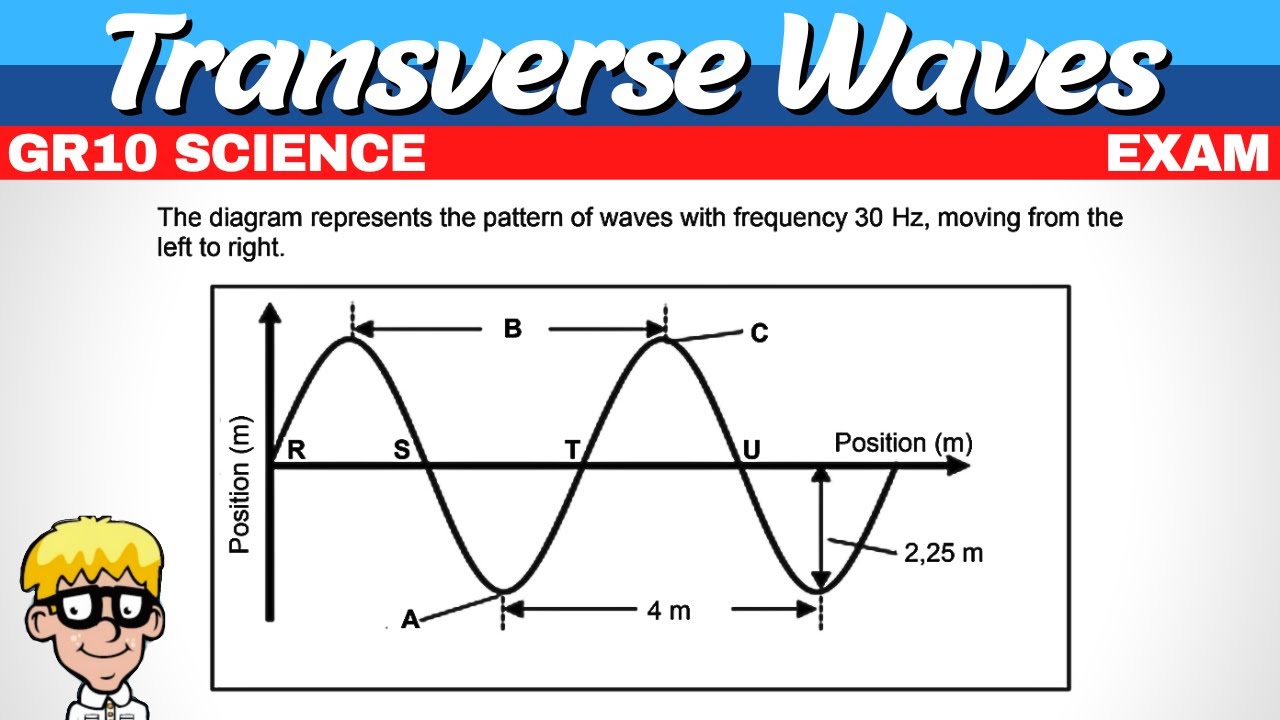
  • 🌊 Wavelength is the distance between the crests of a wave, measured in meters (m), symbolized by the Greek letter 'λ' (lambda).
  • ⏲ Frequency is how many times a wave passes a certain point in a given time, measured in hertz (Hz) and symbolized by 'f'.
  • 🧮 The formula for wave speed is v = λ * f.
  • 📊 Example: A wave with a wavelength of 14.5 meters and a frequency of 28.6 Hz has a speed of 414.7 m/s.
  • 📝 To find the wavelength given the speed and frequency, rearrange the formula to λ = v / f.
  • 📐 Example: A wave with a speed of 45.6 m/s and a frequency of 9.6 Hz has a wavelength of 4.8 meters.
  • 📡 To find the frequency given the speed and wavelength, rearrange the formula to f = v / λ.
  • 💡 Example: A light wave traveling at 300 million m/s with a wavelength of 212 meters has a frequency of 1,415,094.3 Hz.
Q & A

  • What is the formula for calculating a wave's speed given its frequency and wavelength?

    -The formula is v = λ * f, where v is the speed of the wave, λ (lambda) is the wavelength, and f is the frequency.

  • How is speed defined in the context of wave calculations?

    -Speed is how fast the wave is traveling, measured in meters per second (m/s).

  • What are the symbols used for speed, wavelength, and frequency in wave equations?

    -The symbol for speed is either 'v' for velocity or 's'. The symbol for wavelength is λ (lambda), and the symbol for frequency is 'f'.

  • How is wavelength defined and measured?

    -Wavelength is the distance between the crest of one wave to the crest of the next, measured in meters (m).

  • What is frequency and how is it measured?

    -Frequency is how many times the wave passes a certain point in a given reference of time, measured in hertz (Hz).

  • What is the speed of a wave with a wavelength of 14.5 meters and a frequency of 28.6 hertz?

    -The speed of the wave is 414.7 meters per second, calculated by multiplying the wavelength (14.5 m) by the frequency (28.6 Hz).

  • How do you solve for wavelength if given the speed and frequency of a wave?

    -To solve for wavelength (λ), use the formula λ = v / f, where v is the speed of the wave and f is the frequency.

  • Given a wave with a frequency of 9.6 hertz and traveling at a speed of 45.6 meters per second, what is the wavelength?

    -The wavelength is 4.8 meters, calculated by dividing the speed (45.6 m/s) by the frequency (9.6 Hz) and rounding to one decimal place.

  • What is the frequency of a light wave traveling at 300 million meters per second with a wavelength of 212 meters?

    -The frequency is 1,415,094.3 hertz, calculated by dividing the speed (300 million m/s) by the wavelength (212 m).

  • Why is the speed of light considered constant in this example?

    -All visible light travels at the same speed, which is approximately 300 million meters per second, in a vacuum.

Outlines
00:00
🌊 Introduction to Wave Speed, Wavelength, and Frequency

In this paragraph, the instructor introduces the fundamental concepts of wave speed, wavelength, and frequency. They explain that speed measures how fast a wave travels and is denoted by 'v' or 's' in meters per second. The distance between consecutive wave crests defines the wavelength, symbolized by the Greek letter 'lambda' (λ), measured in meters. Frequency, denoted by 'f', indicates how often the wave passes a point within a specific time frame, measured in hertz (Hz). The formula connecting these quantities is introduced: speed (v) equals wavelength (λ) times frequency (f).

05:04
🧮 Calculating Wavelength Using Frequency and Speed

The instructor provides an example problem to calculate the wavelength when given the frequency and speed of a wave. They detail the steps to isolate the wavelength (λ) by rearranging the speed equation, v = λf, to λ = v/f. Using the given values (speed of 45.6 m/s and frequency of 9.6 Hz), the calculation yields a wavelength of 4.8 meters. This example demonstrates the application of algebra to solve for different wave properties using the provided formula.

10:05
🔢 Determining Frequency from Speed and Wavelength

This paragraph focuses on finding the frequency of a light wave, given its speed and wavelength. The example involves a light wave traveling at 300 million meters per second with a wavelength of 212 meters. The formula f = v/λ is used to determine the frequency. The calculation results in a frequency of 1,415,094.3 Hz, illustrating the concept with visible light's high speed and how frequency and wavelength are related. The instructor emphasizes the importance of understanding these concepts for solving practice questions and preparing for an upcoming quiz.

Mindmap
Keywords
💡Wave speed
Wave speed is the rate at which a wave travels through a medium, measured in meters per second (m/s). In the video, wave speed is calculated using the formula v = λ * f, where λ is the wavelength and f is the frequency. Understanding wave speed is crucial for determining how quickly a wave propagates from one point to another.
💡Frequency
Frequency refers to the number of wave cycles that pass a fixed point per second, measured in Hertz (Hz). The video explains that frequency is symbolized by 'f' and highlights its importance in calculating wave speed. For example, a wave with a frequency of 28.6 Hz is used to determine the wave speed in one of the examples.
💡Wavelength
Wavelength is the distance between successive crests (or troughs) of a wave, measured in meters (m). It is symbolized by the Greek letter lambda (λ). The video illustrates how to calculate wavelength when given the wave speed and frequency, emphasizing its role in wave mechanics.
💡Velocity
Velocity, often used interchangeably with speed in the context of waves, is the rate of change of an object's position. The video uses 'v' for velocity and describes it as how fast the wave is traveling. It also differentiates between speed and velocity, noting that while they are closely related, they are not exactly the same.
💡Heinrich Hertz
Heinrich Hertz was a German physicist who made significant contributions to the understanding of electromagnetic waves. The unit of frequency, Hertz (Hz), is named after him. The video references Hertz when explaining the measurement of frequency, showing his impact on wave physics.
💡Meters per second (m/s)
Meters per second is the unit of measurement for speed, indicating how many meters a wave travels in one second. The video uses this unit to express wave speed, such as calculating a wave speed of 414.7 m/s from a given wavelength and frequency.
💡Lambda (λ)
Lambda (λ) is the Greek symbol used to represent wavelength in wave equations. The video demonstrates how to isolate and solve for λ when given the other variables, making it a central concept in understanding wave properties.
💡Hertz (Hz)
Hertz (Hz) is the unit of frequency, representing the number of cycles per second. The video explains that frequency, symbolized by 'f', is measured in Hertz and is essential for calculating wave speed and wavelength. For example, a frequency of 28.6 Hz is used in the calculation of wave speed.
💡Meters (m)
Meters is the unit of measurement for both wavelength and distance. The video consistently uses meters to quantify the distance between wave crests (wavelength) and the speed at which waves travel. This unit is crucial for accurate calculation and understanding of wave mechanics.
💡Simple algebra
Simple algebra refers to the basic mathematical operations used to solve for one variable when given others. The video emphasizes that calculating wave speed, wavelength, and frequency involves straightforward algebraic manipulations, making it accessible to students familiar with basic algebra.
Highlights

Introduction to calculating wave speed, frequency, and wavelength.

Explanation of speed as the measure of how fast the wave is traveling in meters per second.

Description of speed and velocity being closely related.

Definition of wavelength as the distance between the crest of one wave to the crest of the next, measured in meters.

Introduction of the Greek symbol lambda (λ) to represent wavelength.

Explanation of frequency as the number of times a wave passes a certain point in a given time frame, measured in hertz (Hz).

Introduction of the formula for wave speed: v = λ * f.

Example problem: Calculating the speed of a wave with a given wavelength and frequency.

Step-by-step solution of the example problem using the formula v = λ * f.

Introduction of another example: Calculating the wavelength given speed and frequency.

Explanation of isolating the wavelength variable in the formula.

Step-by-step solution of the second example problem using the modified formula λ = v / f.

Introduction of a third example: Calculating the frequency given speed and wavelength.

Explanation of isolating the frequency variable in the formula.

Step-by-step solution of the third example problem using the modified formula f = v / λ.

Discussion on the speed of light and its relation to frequency and wavelength in the example.

Encouragement to use the video to solve practice questions and prepare for an upcoming quiz.

Transcripts

Browse More Related Video

Grade 10 Physics Wave Speed

Exam Transverse Waves Grade 10

EM waves: wavelength, amplitude, frequency, and Hertz

Wavelength-Frequency equation

Transverse Waves Grade 10

Waves - Frequency, Speed, and Wavelength (NEWER vid)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Wave SpeedFrequencyWavelengthPhysicsEducationAlgebraScienceHertzVelocityFormula