Grade 10 Physics Wave Speed

Miss Martins Maths and Science
31 Jan 202412:25
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Miss Martin explores the concept of wave speed, explaining its definition as the distance a wave travels per unit time. She emphasizes the importance of understanding related wave properties like wavelength, frequency, and period, and provides the formula for calculating wave speed: V = f × λ, where V is speed in meters per second, f is frequency in hertz, and λ is wavelength in meters. The video includes practical examples and exercises to demonstrate the application of this formula, ensuring viewers grasp the fundamental principles of wave motion.

Takeaways
  • 📚 The video is about understanding wave speed, its definition, and how to calculate it.
  • 🔍 To grasp wave speed, one must first understand other wave properties like wavelength, frequency, and period.
  • 🔢 Wave speed (V) is defined as the distance traveled by points on a wave per unit time, and it's typically measured in meters per second (m/s).
  • 📐 The formula for wave speed is V = f * λ, where f is the frequency in hertz (Hz) and λ (lambda) is the wavelength in meters.
  • 📚 The standard units for wave speed are meters per second (m/s), which is derived from the units of frequency and wavelength.
  • 🧩 It's important to understand that 'per unit time' in the definition means dividing by time, which is implicitly represented in the formula through the reciprocal relationship between frequency and period.
  • 🔄 The relationship between frequency and period is that they are reciprocals of each other, with the formula for frequency being 1 over the period.
  • 📝 In exams, knowing the definition of wave speed and being able to apply the formula V = f * λ is crucial.
  • 📉 When given a diagram of a wave, one can determine the wavelength by measuring the distance between two consecutive crests or troughs.
  • 📌 If the speed and wavelength of a wave are known, the frequency can be calculated using the formula f = V / λ.
  • ⏱ The period of a wave can be found by taking the reciprocal of the frequency, which is T = 1 / f.
  • 🔑 Units are essential; for example, if the speed is in meters per second, the wavelength must be in meters for the formula to work correctly.
Q & A

  • What is the definition of wave speed?

    -Wave speed is the distance traveled by points on a wave per unit time.

  • Why is the symbol 'V' used to represent wave speed in the formula?

    -The symbol 'V' is used because it stands for velocity, which is similar to speed in physics. It will be explained in more detail in mechanics, but for now, it represents speed.

  • What are the standard units for wave speed?

    -The standard units for wave speed are meters per second (m/s).

  • How is the frequency of a wave related to its period?

    -Frequency and period are reciprocals of each other. The formula for frequency is 1 over the period.

  • What is the formula for calculating wave speed?

    -The formula for calculating wave speed is V = f * λ, where V is wave speed, f is frequency, and λ (Lambda) is wavelength.

  • What does the symbol λ represent in the context of waves?

    -The symbol λ (Lambda) represents the wavelength of a wave.

  • How can you find the wavelength from a diagram?

    -You can find the wavelength from a diagram by measuring the distance between two consecutive crests or troughs, which is the distance from one peak to the next peak or one trough to the next trough.

  • What is the significance of the negative exponent in the unit m/s?

    -The negative exponent indicates that the unit is the reciprocal of seconds, which is necessary because wave speed is calculated as distance divided by time.

  • How can you calculate the frequency of a wave if you know its speed and wavelength?

    -You can calculate the frequency of a wave by dividing the wave speed by the wavelength, using the formula f = V / λ.

  • What is the relationship between frequency and period of a wave?

    -The relationship between frequency and period is that the period is the reciprocal of the frequency, which can be expressed as T = 1 / f.

  • Why is it important to include units when calculating wave speed or frequency?

    -Including units is important to ensure the calculations are dimensionally correct and to avoid losing marks in exams where unit correctness is assessed.

Outlines
00:00
📚 Introduction to Wave Speed

This paragraph introduces the topic of wave speed, emphasizing the importance of understanding other wave properties such as wavelength, frequency, and period before delving into wave speed calculations. The script mentions that previous videos cover these concepts and provides a link in the description for reference. The definition of wave speed is presented as the distance traveled by points on a wave per unit time, and the formula for wave speed is introduced with an explanation of the symbols used, including 'V' for velocity, 'f' for frequency in hertz, and 'λ' (Lambda) for wavelength in meters. The standard unit for wave speed is highlighted as meters per second (m/s).

05:02
🔍 Calculating Wave Speed and Understanding Formulas

The second paragraph delves deeper into the calculation of wave speed, explaining the relationship between frequency, wavelength, and wave speed. It clarifies that the formula for wave speed is the product of frequency and wavelength, which results in a unit of meters per second (m/s). The script also discusses the concept of frequency being the reciprocal of the period, and how this relationship can be used to further understand wave speed calculations. Practical examples are given, including how to determine wavelength from a diagram and how to apply the formula to calculate wave speed when given frequency and wavelength. The importance of units is stressed, particularly ensuring that wavelength is in meters and frequency in hertz to correctly calculate wave speed in meters per second.

10:03
📘 Applying Wave Speed Formulas to Example Problems

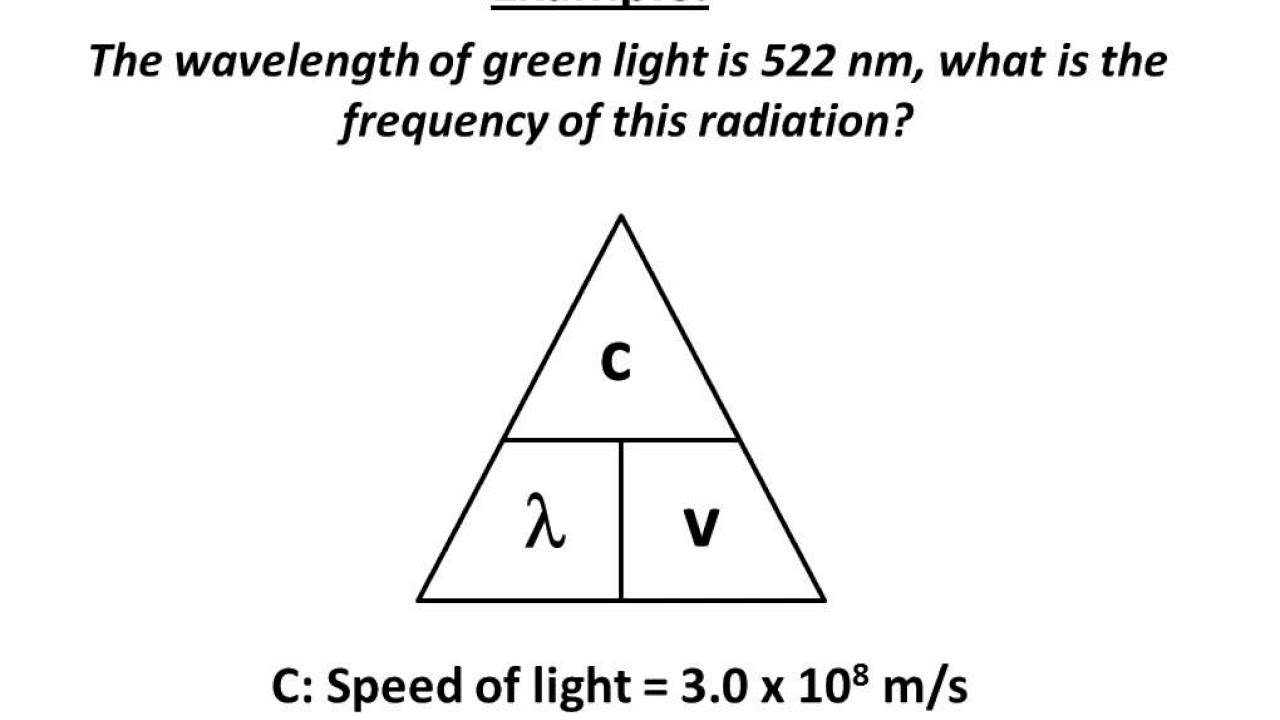
In the final paragraph, the script applies the concepts and formulas discussed to solve example problems. It demonstrates how to find wave speed given frequency and wavelength, and how to calculate frequency and period when wave speed and wavelength are provided. The process of substitution into the formula is explained, and the importance of showing calculations and including units in the final answer is emphasized. The script also touches on the concept of rounding off to two decimal places for period calculations. The paragraph concludes with a reminder of the importance of understanding these concepts for exams and a teaser for upcoming videos that will include practice exam questions.

Mindmap
Keywords
💡Wave Speed
Wave speed is the distance traveled by points on a wave per unit time. It is a fundamental concept in physics that helps to understand how waves propagate through different media. In the video, wave speed is represented by the variable 'V' and is calculated using the formula V = f * λ, where 'f' is the frequency of the wave and 'λ' (lambda) is the wavelength. The script emphasizes the importance of knowing how to calculate wave speed for various physics problems.
💡Frequency (f)
Frequency in the context of waves refers to the number of oscillations or cycles a wave completes in one second, measured in hertz (Hz). It is a key component in calculating wave speed, as demonstrated in the formula V = f * λ. The video script uses the frequency of a wave as an example to show how to determine wave speed when given the frequency and wavelength.
💡Wavelength (λ)
Wavelength is the spatial period of a wave, which is the distance between two consecutive points in phase on the wave, such as from crest to crest. It is denoted by the Greek letter lambda (λ) and is measured in meters. The script explains how to find the wavelength from a diagram and uses it in the calculation of wave speed.
💡Transverse Wave
A transverse wave is a type of wave where the displacement of the medium is perpendicular to the direction of the wave's propagation. The video script mentions a transverse wave in the context of a diagram provided to help understand the concept of wavelength and how to measure it.
💡Velocity
Although not explicitly defined in the script, velocity is closely related to wave speed. Velocity is a vector quantity that includes both speed and direction, whereas wave speed is a scalar quantity, indicating how fast the wave travels without regard to direction. The script uses 'V' to denote wave speed, which is a form of velocity specific to waves.
💡Hertz (Hz)
Hertz is the unit of measurement for frequency, indicating the number of cycles per second. The script mentions that frequency is measured in hertz and uses this unit in the formula for calculating wave speed.
💡Meters per Second (m/s)
Meters per second is the standard unit for measuring speed, including wave speed. The script explains that wave speed is calculated in meters per second, which is derived from the formula involving frequency in hertz and wavelength in meters.
💡Reciprocal
In mathematics, reciprocal refers to a number which, when multiplied by the original number, results in one. The script mentions that frequency and period are reciprocals of each other, meaning if you have the frequency, you can find the period by taking the reciprocal.
💡Period
The period of a wave is the time taken for one complete cycle of the wave to occur. It is the reciprocal of frequency and is measured in seconds. The script explains how to calculate the period from the frequency and emphasizes the importance of including units in the final answer.
💡Mechanics
Mechanics is a branch of physics that deals with the motion of objects and the forces that cause motion. The script mentions that the concept of velocity, as used in wave speed, will be further explored in the mechanics section, indicating that a deeper understanding of these concepts is part of a broader study in physics.
💡Scalar and Vector Quantities
Scalar quantities have only magnitude, while vector quantities have both magnitude and direction. The script implies this distinction by mentioning that 'V' for wave speed is a scalar, whereas velocity, which includes direction, is a vector.
Highlights

Introduction to wave speed and its importance in understanding waves.

Explanation of prerequisites such as wavelength, frequency, and period before diving into wave speed calculations.

Wave speed defined as the distance traveled by points on a wave per unit time.

Clarification on the use of 'V' for velocity in physics and its relation to wave speed.

The formula for wave speed is presented as V = f * λ, where V is speed, f is frequency, and λ is wavelength.

Units of wave speed are meters per second (m/s), emphasizing the importance of units in physics calculations.

Understanding the relationship between frequency and period as reciprocals to grasp wave speed calculations.

Demonstration of how to manipulate the wave speed formula to include frequency and period.

The significance of the negative exponent in the unit m/s explained through the division by time.

A step-by-step guide on how to calculate wave speed using the given formula and units.

Use of a diagram to determine wavelength when calculating wave speed, emphasizing the importance of visual aids in physics.

Example problem walkthrough: Calculating wave speed given frequency and the diagram of a transverse wave.

Another example problem: Determining frequency of a wave when given wave speed and wavelength.

The concept of reciprocal relationship between frequency and period, and how to calculate period from frequency.

Emphasis on the importance of including units in final answers for physics problems.

The rounding rule in science to round off to at least two decimal places for precise measurements.

Encouragement to review previous videos for a comprehensive understanding of waves before moving on to wave speed.

Promise of upcoming videos that will cover practice exam questions related to wave speed.

Transcripts

Browse More Related Video

How to calculate wave speed, wavelength, and frequency.

Wavelength-Frequency equation

Waves - Frequency, Speed, and Wavelength (NEWER vid)

EM waves: wavelength, amplitude, frequency, and Hertz

Wave Speed Practice Problems v2

💯 Wave Terminology #3/5 Period and Frequency

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Wave SpeedPhysics EducationFrequencyWavelengthVelocityHertzMeters per SecondTransverse WavesCalculation GuideEducational VideoScience Tutorial