Wavelength-Frequency equation

Marie Stott
27 Sept 201205:30
EducationalLearning
32 Likes 10 Comments

TLDRMr. T guides students through the equation relating the speed of light, frequency, and wavelength. He explains that the speed of light (C) is a constant at 3.0 x 10^8 meters per second, frequency (V) is measured in Hertz, and wavelength (λ) in meters or nanometers. Using a triangle diagram, he shows how to solve for frequency or wavelength. He provides an example problem, converting wavelength from nanometers to meters, and calculates the frequency of green light, emphasizing the importance of unit consistency and significant figures.

Takeaways
  • 📏 The speed of light, denoted as C, is a constant value of 3.0 × 10⁸ meters per second.
  • 🎚️ Frequency (V) is measured in Hertz (Hz) or seconds⁻¹.
  • 🌊 Wavelength (λ), represented by the lambda symbol (an inverted Y), is measured in meters or nanometers.
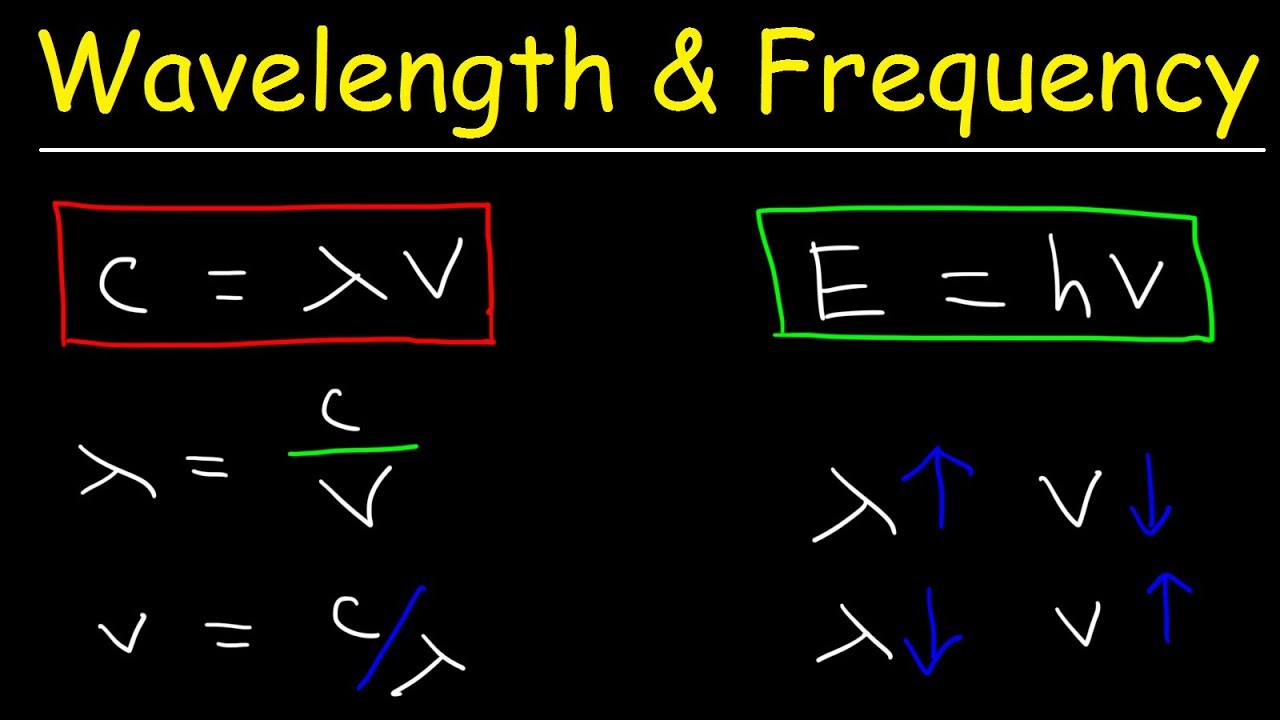
  • 🔺 The relationship between speed of light (C), frequency (V), and wavelength (λ) is represented in a triangle format.
  • 🔍 To solve for frequency, use the formula V = C / λ.
  • 📝 To solve for wavelength, use the formula λ = C / V.
  • 📉 In problem-solving, ensure that units are consistent; convert wavelengths to meters if needed.
  • 🔄 Conversion factor for nanometers to meters: 1 meter = 10⁹ nanometers.
  • 🧮 Dimensional analysis is used to convert units, ensuring calculations are accurate.
  • 🎯 Always express final answers with the correct number of significant figures, based on the given data.
Q & A

  • What is the constant C in the context of the equation discussed in the script?

    -In the script, C represents the speed of light, which is a constant value of 3.0 times 10 to the 8th meters per second.

  • What does the variable V stand for in the equation?

    -V stands for the frequency of a wave, measured in Hertz, which is equivalent to cycles per second or seconds to the minus 1.

  • What is the symbol lambda (λ) used to represent in the script?

    -The symbol lambda (λ) is used to represent the wavelength of a wave, which can be expressed in units of meters or nanometers.

  • How are the variables C, V, and λ related in the equation discussed in the script?

    -The variables are related through the equation C = V * λ, where C is the speed of light, V is the frequency, and λ is the wavelength.

  • What is the significance of the triangle mentioned in the script when solving problems with the equation?

    -The triangle is a visual aid to remember the relationship between the speed of light (C), frequency (V), and wavelength (λ), helping to identify which variables are known and which need to be found.

  • What is the first step to consider when solving a problem using the equation?

    -The first step is to determine what variable you are trying to find, whether it's the frequency (V), the wavelength (λ), or the speed of light (C).

  • How do you find the frequency if you know the speed of light and the wavelength?

    -To find the frequency, use the equation V = C / λ, where C is the speed of light and λ is the wavelength.

  • How do you find the wavelength if you know the speed of light and the frequency?

    -To find the wavelength, use the equation λ = C / V, where C is the speed of light and V is the frequency.

  • What is the example problem presented in the script?

    -The example problem asks for the frequency of green light given that its wavelength is 522 nanometers.

  • Why is unit conversion necessary in the example problem, and how is it done?

    -Unit conversion is necessary because the wavelength is given in nanometers while the speed of light is in meters. The conversion is done by dividing the wavelength in nanometers by 10 to the 9th power to get the value in meters.

  • What is the result of the example problem, and how many significant figures should it have?

    -The result of the example problem is a frequency of 5.75 times 10 to the 14th Hertz. It should have three significant figures, matching the number of significant figures in the given wavelength.

Outlines
00:00
🔬 Understanding the Speed of Light Equation

Mr. T introduces the fundamental equation relating the speed of light (C), frequency (V), and wavelength (λ). The speed of light (3.0 x 10^8 meters per second) is a constant. Frequency is measured in Hertz, and wavelength is in meters or nanometers. Mr. T explains the triangle method for solving problems involving these variables. When solving for frequency (V), you divide the speed of light (C) by the wavelength (λ). Similarly, when solving for wavelength (λ), you divide the speed of light (C) by the frequency (V).

05:01
📏 Example Problem: Calculating Frequency from Wavelength

Mr. T provides an example problem where the wavelength of green light (522 nanometers) is used to find the frequency. He highlights the importance of unit conversion, converting nanometers to meters by using the conversion factor (1 meter = 10^9 nanometers). After converting, he uses the triangle method to solve for the frequency. The final step involves calculating and expressing the answer in scientific notation, ensuring that the significant figures are correct. The example yields a frequency of 5.75 x 10^14 Hertz.

🔢 Significant Figures in Calculations

Mr. T emphasizes the importance of significant figures in the final answer. The wavelength value (522 nanometers) has three significant figures, so the final answer should also reflect this. Constants, such as the speed of light, are not considered when counting significant figures for the final result. This attention to detail ensures accuracy and consistency in scientific calculations.

Mindmap
Keywords
💡Speed of light (C)
The speed of light, denoted as 'C', is a fundamental constant in physics with a value of approximately 3.0 x 10^8 meters per second. In the context of the video, it represents a crucial part of the equation that relates speed, frequency, and wavelength. This constant is pivotal as it allows for the calculation of one variable when the other two are known, such as finding the frequency when given the wavelength.
💡Frequency (V)
Frequency, represented as 'V', refers to the number of wave cycles that pass a point per second, measured in Hertz (Hz). In the video, frequency is one of the key variables in the equation that relates to the speed of light and wavelength. The video explains how to solve for frequency using the equation V = C / λ, making it a central concept in understanding how light waves behave.
💡Wavelength (λ)
Wavelength, denoted by the Greek letter 'λ' (lambda), is the distance between successive peaks of a wave, typically measured in meters or nanometers. In the video, wavelength is one of the three variables in the equation that correlates with the speed of light and frequency. The explanation emphasizes the importance of converting wavelength into compatible units when using the equation.
💡Equation triangle
The equation triangle is a mnemonic tool used to help students remember the relationship between the speed of light (C), frequency (V), and wavelength (λ). In the video, this triangle is shown with C on top, and V and λ on the bottom, making it easy to derive the equations V = C / λ and λ = C / V depending on what needs to be calculated.
💡Nanometers
Nanometers (nm) are a unit of length in the metric system, equal to one billionth of a meter (10^-9 meters). In the video, nanometers are used to measure the wavelength of light. The explanation includes a step on how to convert nanometers to meters for consistency in calculations involving the speed of light.
💡Dimensional analysis
Dimensional analysis is a method used in science and engineering to convert units and check the consistency of equations. In the video, dimensional analysis is applied to convert the wavelength from nanometers to meters, ensuring that all units match before plugging them into the equation to find frequency.
💡Significant figures
Significant figures refer to the digits in a number that are reliable and necessary to indicate the precision of a measurement. In the video, the importance of significant figures is highlighted when expressing the final answer for frequency. The example given emphasizes matching the number of significant figures in the calculated result with the given data.
💡Conversion factor
A conversion factor is a numerical ratio used to convert a quantity from one unit to another. In the video, a conversion factor of 1 meter = 10^9 nanometers is used to convert the wavelength from nanometers to meters, which is necessary for accurately solving the equation with the speed of light.
💡Meters per second
Meters per second (m/s) is the SI unit of speed or velocity, indicating how many meters an object or wave travels in one second. In the video, this unit is used for the speed of light, providing a basis for calculating the frequency or wavelength of light waves.
💡Hertz
Hertz (Hz) is the unit of frequency, representing the number of cycles per second. In the context of the video, hertz is used to express the frequency of light after solving the equation. This term helps viewers understand the measurement and implications of wave frequencies in the context of light and other electromagnetic waves.
Highlights

Introduction to the equation correlating the speed of light, frequency, and wavelength.

Explanation of the constant speed of light, C, as 3.0 x 10^8 meters per second.

Definition of V as frequency in Hertz and lambda as wavelength in meters or nanometers.

Introduction of the triangle method to correlate C, V, and lambda.

Guidance on determining what variable to find based on the given problem.

How to derive the equation for frequency V when given C and lambda.

Derivation of the equation for wavelength lambda when given C and V.

Example problem: Finding the frequency of green light with a given wavelength.

Emphasis on the constant value of the speed of light in all problems.

The importance of unit conversion from nanometers to meters for accurate calculations.

Conversion factor explanation: 1 meter equals 10^9 nanometers.

Demonstration of dimensional analysis for unit conversion.

Calculation of frequency using the speed of light and converted wavelength.

Cancellation of units in the equation for simplified calculation.

Final result calculation and its significance in Hertz.

Importance of expressing results with the correct number of significant figures.

Clarification that constants do not affect the count of significant figures.

Transcripts

Browse More Related Video

💯 Wave Terminology #3/5 Period and Frequency

Frequency, Wavelength, and the Speed of Light

Grade 10 Physics Wave Speed

Speed of Light, Frequency, and Wavelength Calculations - Chemistry Practice Problems

How to calculate wave speed, wavelength, and frequency.

Wave Speed

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Light SpeedFrequencyWavelengthPhysicsEducationalOpticsHertzMeters per SecondNanometersConversionSignificant Figures