Two Slit Interference | Physics with Professor Matt Anderson | M28-18

Physics with Professor Matt Anderson
15 Mar 202212:16
EducationalLearning
32 Likes 10 Comments

TLDRThe script explores a multi-color double-slit experiment, delving into the physics of light diffraction. It contrasts the diffraction patterns of red (900 nm) and blue (750 nm) light, highlighting how they differ due to wavelength. The presenter guides viewers through the calculation to find where the bright fringes of the two patterns coincide, using the formula d * sin(ΞΈ) = m * Ξ». The engaging explanation simplifies complex concepts, making physics accessible and intriguing.

Takeaways
  • πŸ§ͺ The script discusses a physics experiment involving a double-slit setup with two different wavelengths of light.
  • 🌈 The experiment uses two colors, red and blue, to explore the diffraction patterns created by the double-slit setup.
  • πŸ” The script clarifies that the colors used (750 nm and 900 nm) do not correspond to the actual colors of red and blue but are used for illustrative purposes.
  • πŸ“ The separation between the slits is given as two millimeters, and the screen is placed two meters away from the slits.
  • πŸ€” The main question posed is to find where the bright fringes from the two different patterns will first coincide on the screen.
  • πŸ“š The script explains the relationship between wavelength, slit separation, and the angle of the maxima using the formula d * sin(ΞΈ) = m * Ξ».
  • πŸ”’ It is determined that the ratio of the order of maxima for red to blue light is 1.2, indicating that the maxima will not align in a simple integer ratio.
  • πŸ”„ The script suggests that the sixth bright fringe of the blue light will coincide with the fifth bright fringe of the red light.
  • πŸ“ Using trigonometry and the given values, the script calculates the distance from the central maximum where the bright fringes will coincide.
  • πŸ“ The final calculation results in a distance of 4.5 millimeters from the central maximum for the bright fringes to coincide.
  • πŸ’‘ The script concludes by emphasizing the multi-color approach to the double-slit experiment, adding a layer of complexity and interest to the physics concept.
Q & A

  • What is the main topic discussed in the script?

    -The main topic discussed in the script is the double-slit experiment with two different wavelengths of light.

  • What are the two wavelengths of light used in the experiment described in the script?

    -The two wavelengths of light used in the experiment are 750 nanometers (nm) and 900 nm.

  • What is the distance between the slits in the double-slit experiment mentioned in the script?

    -The distance between the slits in the double-slit experiment is two millimeters.

  • How far is the screen placed from the slits in the experiment?

    -The screen is placed two meters from the slits.

  • What is the relationship between the wavelength of light and the angle of the maxima in a double-slit experiment?

    -In a double-slit experiment, a longer wavelength of light results in a larger angle for the maxima due to the equation d * sin(theta) = m * lambda, where d is the distance between slits, theta is the angle, m is the order of the maxima, and lambda is the wavelength.

  • What is the significance of the equation d * sin(theta) = m * lambda in the context of the script?

    -This equation is used to determine the positions of the bright fringes or maxima in a double-slit experiment. It relates the distance between the slits, the angle of the maxima, the order of the maxima, and the wavelength of the light.

  • How does the script differentiate between the maxima of the blue and red light patterns in the experiment?

    -The script differentiates by labeling the angles for the blue and red light patterns as theta for blue (theta_b) and theta for red (theta_r), and then finding the condition where these angles are equal for the maxima to overlap.

  • What is the ratio of the maxima orders (m) for the red and blue light when they first coincide in the experiment?

    -The ratio of the maxima orders for the red and blue light when they first coincide is 6/5, meaning the sixth fringe of the blue pattern overlaps with the fifth fringe of the red pattern.

  • How is the distance from the central maximum to the point where the bright fringes from both patterns coincide calculated?

    -The distance is calculated using the formula y_m = (m * lambda * L) / d, where m is the order of the maxima, lambda is the wavelength, L is the distance from the slits to the screen, and d is the distance between the slits.

  • What is the final answer for the distance in millimeters from the central maximum to the point of coincidence of the bright fringes?

    -The final answer for the distance is 4.5 millimeters.

  • What is the small angle approximation used in the script to simplify the calculation?

    -The small angle approximation used in the script is sin(theta) β‰ˆ y_m / L, which simplifies the calculation of the position of the maxima on the screen.

Outlines
00:00
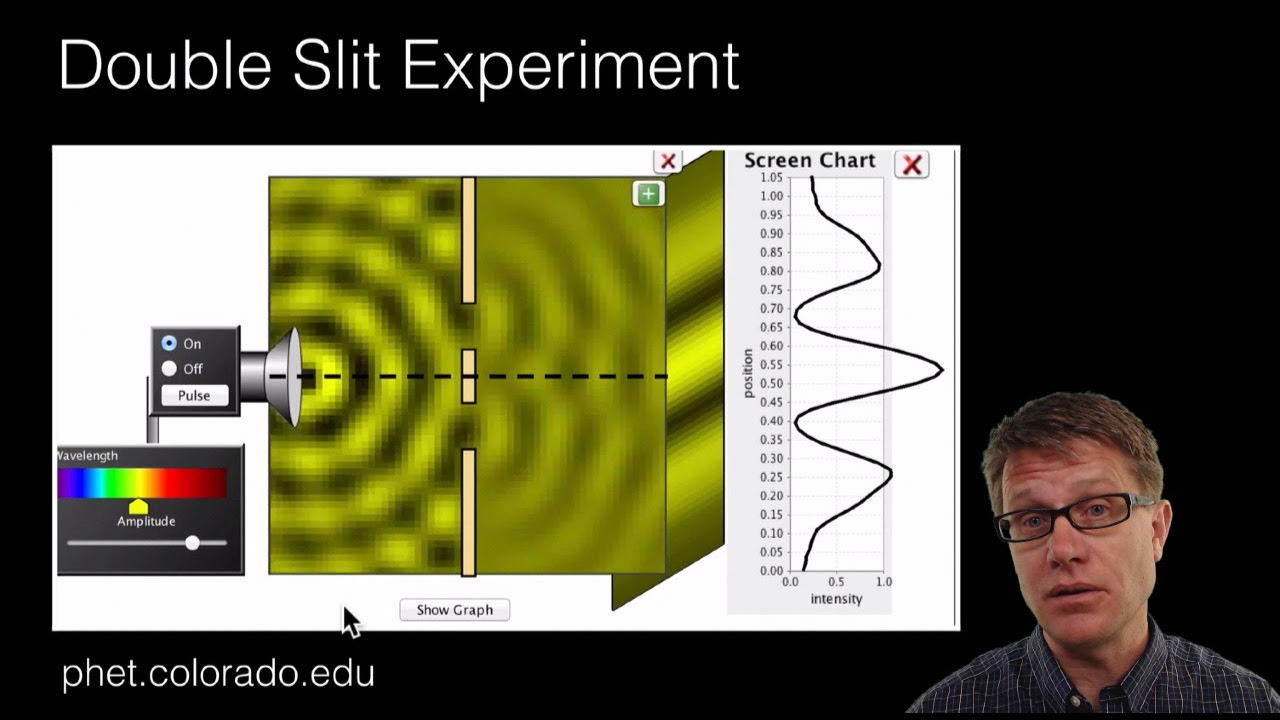
πŸ”¬ Double Slit Experiment with Wavelengths

This paragraph discusses a physics experiment involving the double slit phenomenon with two different wavelengths of light. The focus is on the setup where two slits are separated by two millimeters and light with wavelengths of 750 nm (blue) and 900 nm (red) is used to illuminate them. The goal is to determine where the bright fringes from the two different patterns will first coincide on a screen placed two meters away. The explanation involves understanding the diffraction pattern and the relationship between wavelength, slit separation, and the angle at which the bright fringes appear.

05:01
πŸ“ Calculating the Overlap of Fringe Patterns

The second paragraph delves into the calculation of when the bright fringes from the two different colors of light will align. It explains that the alignment occurs when the angles for the red and blue light are equal, leading to the equation sine(theta_r) = sine(theta_b). By using the double-slit formula d * sine(theta) = m * lambda, and considering the different wavelengths, the ratio of the order of maxima (m) for red to blue is calculated to be 1.2. The paragraph then explores the integer values of m that would satisfy this ratio, concluding that the sixth bright fringe of the blue pattern will coincide with the fifth of the red pattern.

10:02
πŸ“ Determining the Distance of Coinciding Fringe

The final paragraph focuses on finding the exact distance from the central maximum on the screen where the bright fringes from the two patterns will coincide. Using the small angle approximation, the equation d * y_m / L = m * lambda is rearranged to solve for y_m, the distance of the m-th bright fringe from the central maximum. The values for m (5 for the red pattern), lambda (900 nm), L (2 meters), and d (2 mm) are substituted into the equation, leading to a calculation that results in a distance of 4.5 millimeters where the bright fringes will first coincide.

Mindmap
Keywords
πŸ’‘Double Slit Experiment
The double slit experiment is a classic physics demonstration that explores the wave-particle duality of light and other quantum particles. It involves shining light through two closely spaced slits and observing the interference pattern that forms on a screen behind the slits. In the video, this experiment is used to illustrate how different wavelengths of light create different interference patterns, with the script discussing the specific case of red and blue light.
πŸ’‘Wavelength
Wavelength is the distance between two consecutive points in a wave that are in the same phase, such as from crest to crest. It is a fundamental property of waves and determines their color in the case of visible light. In the script, the wavelengths of 750 nanometers (nm) for blue light and 900 nm for red (near-infrared) light are key to calculating the positions of the bright fringes in the double slit experiment.
πŸ’‘Diffraction Pattern
A diffraction pattern is the graphical representation of how waves spread out after passing through an obstacle or a slit. In the context of the video, the diffraction pattern is observed on the screen after light passes through the two slits. The pattern consists of alternating bright and dark regions, which are the result of constructive and destructive interference of the waves.
πŸ’‘Bright Fringe
A bright fringe in an interference pattern is a region of constructive interference, where the waves from the two slits add together to produce a maximum intensity. The script discusses the alignment of bright fringes from two different light patterns, specifically the blue and red light, as part of the double slit experiment.
πŸ’‘Optical Axis
The optical axis is an imaginary line that passes through the center of a lens or mirror and is perpendicular to the surface of the screen where an image is formed. In the video script, the term is used to describe the reference line from which angles to the maxima (bright fringes) are measured in the double slit experiment.
πŸ’‘Maxima
In the context of wave interference, maxima refer to the points of constructive interference where the amplitude of the wave is at its highest. The script uses the term to describe the bright regions in the interference pattern of the double slit experiment and to calculate the positions where the bright fringes from different colors coincide.
πŸ’‘Angle of Incidence
The angle of incidence is the angle at which a wave strikes a surface or passes through an opening. In the script, the angle of incidence is used to describe the angle between the optical axis and the path of the light to a particular maxima in the interference pattern.
πŸ’‘Sine Function
The sine function is a mathematical function that describes a smooth, periodic oscillation. In the script, the sine function is used in the formula to calculate the positions of the maxima in the double slit experiment, relating the angle of incidence to the wavelength and the distance between the slits.
πŸ’‘Interference
Interference is a phenomenon in which two or more waves superimpose to form a resultant wave of greater, lower, or the same amplitude. The script discusses how the interference of light waves from the two slits in the double slit experiment creates the observed pattern of bright and dark fringes.
πŸ’‘Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. In the video script, trigonometry is used to calculate the distance from the central maximum to the point where the bright fringes from the red and blue light patterns coincide in the double slit experiment.
πŸ’‘Small Angle Approximation
The small angle approximation is a simplification used in trigonometry when the angle is very small, allowing the sine of the angle to be approximated as the angle itself (in radians). The script mentions this approximation when calculating the position of the bright fringes on the screen in the double slit experiment.
Highlights

Introduction of a double-slit experiment with two different colors of light.

Exploration of the concept of 'hungry for knowledge' in the context of physics.

Description of the experimental setup with two slits and a distant screen.

Introduction of the two wavelengths used in the experiment: 750 nm and 900 nm.

Explanation of the diffraction pattern produced by the two different wavelengths.

Discussion on the relationship between wavelength and the angle of maxima in the pattern.

Equation for finding the two-slit maxima: d * sin(theta) = m * lambda.

Analysis of the overlap and difference between the red and blue light patterns.

Calculation of the ratio of the maxima for red and blue light.

Determination that the sixth fringe of the blue pattern overlaps with the fifth fringe of the red pattern.

Use of trigonometry to find the distance from the central maximum where the bright fringes coincide.

Derivation of the formula to calculate the distance of the bright fringes: y_m = (m * lambda * L) / d.

Substitution of known values into the formula to calculate the specific distance.

Final calculation resulting in the bright fringes coinciding at a distance of 4.5 millimeters from the central maximum.

Conclusion emphasizing the multi-color approach to the double-slit experiment.

Transcripts

Browse More Related Video

Single Slit Interference | Physics with Professor Matt Anderson | M28-19

Resolving Power of a Telescope | Physics with Professor Matt Anderson | M28-14

Light Is Waves: Crash Course Physics #39

Physics - Diffraction of Light (1 of 4) The Thin Slit

Physics 60 Interference of Light (4 of 8) Young's Double Slit

Interference Patterns

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsDouble-SlitExperimentWavelengthDiffractionFringesOpticsEducationalKnowledgeSpectrumLight