Physics - Optics: Lenses (1 of 4) Converging Lens

Michel van Biezen
30 Apr 201304:45
EducationalLearning
32 Likes 10 Comments

TLDRThis script from an online lecture introduces the concept of thin lenses in optics, focusing on their simplicity compared to thick lenses. It explains the behavior of converging lenses, which have a positive focal length and cause parallel light rays to meet at a focal point. The example demonstrates calculating the image distance and magnification for a lens with a 25 cm focal length and an object placed 100 cm away, resulting in a real, inverted image 33 cm behind the lens, one-third the size of the object. The process illustrates the graphical and mathematical methods for solving lens problems.

Takeaways
  • 🔍 Thin lenses are simpler to analyze compared to thick lenses, focusing on converging and diverging lenses in optics.
  • 🔦 Converging lenses have a positive focal length and cause parallel rays of light to converge at a focal point on the other side of the lens.
  • 🔭 In lens problems, the object is placed in front of the lens and the observer is behind it. A real image is formed when light rays converge on the observer's side.
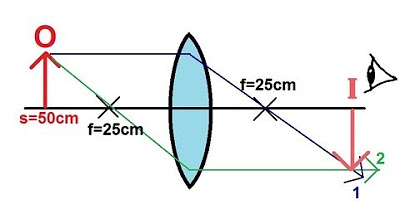
  • 📏 In the given example, an object is placed 100 cm away from a converging lens with a focal length of 25 cm.
  • ✏️ To find the image location graphically, one ray is drawn parallel to the normal and then through the focal point, and another ray through the focal point in front of the lens and then parallel to the normal.
  • 📐 The intersection of these rays indicates the image location, which in this example, is calculated to be 33 cm behind the lens.
  • 🔬 The positive value of the image distance confirms that the image is real and formed on the opposite side of the lens from the object.
  • 📉 The magnification of the image is determined to be -1/3, indicating the image is one-third the size of the object and inverted.
  • 🔄 Moving the object closer to the lens affects the image distance and size, which will be explored in subsequent examples.
  • 🔧 The process of solving lens problems involves using the lens equation and ray diagrams to determine image location, size, and orientation.
Q & A

  • What are thin lenses in the context of optics?

    -Thin lenses are lenses that are considered to have negligible thickness in comparison to other dimensions, simplifying the equations used in optics. If lenses are thick, the equations become more complex.

  • What is the difference between a converging and a diverging lens?

    -A converging lens brings parallel rays of light to a focus on the opposite side, while a diverging lens causes parallel rays to spread out or diverge.

  • Why is the focal length of a lens important?

    -The focal length is the distance from the lens to the point where parallel rays of light converge or appear to diverge. It is a key parameter in determining the lens's ability to form images.

  • What is the focal length of the lens described in the script?

    -The focal length of the lens described in the script is 25 cm.

  • What happens when an object is placed far away from a converging lens?

    -When an object is placed far away from a converging lens, the image formed is close to the focal point and is real, inverted, and smaller than the object.

  • How is the image distance (S') calculated in the script?

    -The image distance (S') is calculated using the lens formula: S' = S * f / (S - f), where S is the object distance, and f is the focal length.

  • What does a positive value of S' indicate about the image formed by the lens?

    -A positive value of S' indicates that the image is real, meaning it is formed on the opposite side of the lens from the object.

  • What is the magnification (m) of the image in the example given, and what does it signify?

    -The magnification (m) in the example is -1/3, indicating that the image is 1/3 the size of the original object and is inverted.

  • What happens to the image as the object is moved closer to the lens?

    -As the object is moved closer to the lens, the image moves further away from the lens, and the size of the image may increase.

  • What is the significance of the normal in the context of lens optics?

    -The normal is a perpendicular line to the lens surface at a given point. Rays parallel to the normal are used to determine the behavior of light when it interacts with the lens.

  • What is the difference between a real and a virtual image?

    -A real image is formed where light rays actually converge, and it can be projected onto a screen. A virtual image is formed where the light rays appear to diverge from, and it cannot be projected onto a screen.

Outlines
00:00
🔎 Introduction to Thin Lenses in Optics

The script introduces the concept of thin lenses in optics, explaining why they are called 'thin' due to the simplicity of their equation compared to thick lenses. It differentiates between converging and diverging lenses, noting that converging lenses focus parallel light rays at a focal point, which is 25 cm away from the lens in the example given. The script also explains the observer's position relative to the lens and the concept of real and virtual images. The first example demonstrates how to graphically determine the image position when an object is placed 100 cm away from the lens, using the lens formula and the properties of light rays.

Mindmap
Keywords
💡Thin Lenses
Thin lenses refer to lenses with negligible thickness in comparison to their focal length, simplifying the optical equations used to describe their behavior. In the video's theme, thin lenses are central to understanding basic optical principles. The script mentions that if lenses are thick, the equations become more complex, hence the focus on thin lenses to simplify the discussion.
💡Converging Lens
A converging lens is an optical device that brings light rays together to a focal point on the opposite side. This concept is fundamental to the video, as it explains how light behaves when passing through a lens. The script uses the example of a lens with a positive focal length of 25 cm, demonstrating how parallel rays converge at the focal point.
💡Focal Length
Focal length is the distance from the center of a lens to the point where light rays parallel to the optical axis converge. It is a key parameter in the script, used to calculate image formation. The script mentions a converging lens with a focal length of 25 cm, which is essential for determining the position and nature of the image formed by the lens.
💡Focal Point
The focal point is the location where light rays converge after passing through a lens. It is a critical concept in the script, as it helps to illustrate the behavior of a converging lens. The script describes how rays parallel to the normal converge at the focal point, which is a defining characteristic of a converging lens.
💡Real Image
A real image is formed when light rays actually converge to form an image on a screen. The script explains that if the light converges to a single point on the other side of the lens, a real image is formed. This is contrasted with a virtual image, which does not converge on a screen but appears to do so.
💡Virtual Image
A virtual image is formed when the extensions of light rays appear to converge, but the rays do not actually meet. The script mentions virtual images in contrast to real images, explaining that different conditions will result in different types of images, with real images being a key focus in the provided examples.
💡Object Distance
Object distance (denoted as 's' in the script) is the distance from the object to the lens. It is a crucial variable in the lens equation and affects the position and size of the image. The script uses an example where the object is placed 100 centimeters away from the lens to illustrate the calculation of image distance.
💡Image Distance
Image distance (denoted as 'S Prime' in the script) is the distance from the lens to the image. The script calculates this distance using the lens equation, which is essential for understanding where the image will form relative to the lens, as demonstrated with the example of an object placed 100 cm away.
💡Magnification
Magnification is the ratio of the image size to the object size, indicating how much larger or smaller the image appears compared to the object. The script calculates magnification using the formula m = -S Prime / s, and finds that the image is 1/3 the size of the object, which also indicates that the image is inverted.
💡Inverted Image
An inverted image is one where the top and bottom of the object are reversed in the image. The script explains that a negative magnification value indicates that the image is inverted, which is a direct result of the lens's optical properties and the position of the object relative to the lens.
💡Lens Equation
The lens equation is a fundamental formula in optics that relates the object distance, image distance, and focal length. The script uses the lens equation (S Prime = S * f / (S - f)) to calculate the position of the image formed by a lens, demonstrating its importance in understanding lens behavior.
Highlights

Introduction to thin lenses in optics, emphasizing their simplicity compared to thick lenses.

Explanation of converging lenses that focus light rays to a point, unlike diverging lenses.

Description of a converging lens with a positive focal length of 25 cm.

Illustration of the lens's symmetry and the presence of focal points on both sides.

The observer's position behind the lens and the concept of real and virtual images.

Graphical method to determine the image formation when the object is far from the lens.

Use of the lens formula S' = S * f / (S - f) to calculate image distance.

Calculation showing the image is 33 cm behind the lens for an object 100 cm away.

Identification of the image as real due to the positive distance behind the lens.

Determination of the image's magnification as 1/3 the size of the object and inverted.

Demonstration of how moving the object closer to the lens affects image distance.

The relationship between object distance and image distance in lens optics.

The significance of the lens's focal length in determining the convergence of light rays.

The impact of object distance on the formation of real versus virtual images.

The practical application of lens optics in imaging systems.

The importance of understanding lens symmetry in optical systems.

The method to graphically trace rays through a lens to predict image formation.

Transcripts

Browse More Related Video

Physics - Optics: Lenses (3 of 4) Converging Lens

Physics - Optics: Lenses (1 of 5) Lens Combinations - Two Converging Lenses

Multiple Two Lens System with Diverging and Converging Lens

Physics - Optics: Lenses (3 of 5) Lens Combinations - Converging & Diverging Lenses

Physics - Optics: Lenses (2 of 4) Converging Lens

Physics - Optics: Lenses (2 of 2) Diverging Lens

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
OpticsLensesConvergenceFocal LengthReal ImageVirtual ImageRay DiagramsMagnificationImaging ProblemsOptical Theory