Physics - Optics: Lenses (2 of 2) Diverging Lens
TLDRThis educational video script explains the behavior of a diverging lens with a negative focal length of -25 cm. It demonstrates how rays diverge from the lens and how the human brain perceives a virtual image, despite the rays not converging. The script also calculates the image distance and magnification using the lens formula, showing that the virtual image is larger and upright compared to the object. The explanation is consistent regardless of the object's position relative to the focal point, emphasizing the lens's effect on image size and orientation.
Takeaways
- 🔍 The video script discusses the behavior of a diverging lens, which has a negative focal length.
- 📏 The focal length of the lens in the example is given as -25 cm.
- 📐 Ray diagrams are used to illustrate how light rays behave when passing through a diverging lens.
- 🌟 When the object is placed inside the focal point, the rays diverge as if they came from the focal point behind the lens.
- 🔄 The observer's brain interprets the diverging rays to form a virtual image, which appears between the object and the lens.
- 📍 The image formation is not affected by whether the object is inside or outside the focal point with a diverging lens.
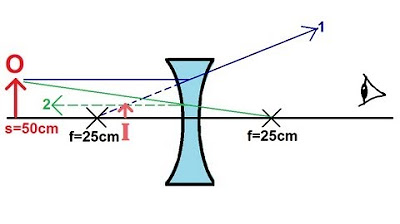
- 🔢 The script uses the lens equation \( S' = \frac{S \cdot f}{s - f} \) to calculate the exact location of the image.
- 📉 The calculated image distance for the given example is -9.375 cm, indicating a virtual image in front of the lens.
- 🔄 The magnification is calculated using the formula \( M = -\frac{S'}{s} \), resulting in a magnification of 0.625 or 62.5% of the original object size.
- 👆 The magnification shows that the image is larger than the object when brought closer to the lens, but still smaller than the original object.
- 🔄 The magnification is positive, indicating that the image is upright.
Q & A
What is the focal length of the diverging lens used in the example?
-The focal length of the diverging lens used in the example is -25 cm.
What happens when an object is placed inside the focal point of a diverging lens?
-When an object is placed inside the focal point of a diverging lens, the rays diverge as if they came from the focal point on the same side of the lens.
How does the brain interpret the diverging rays from a lens?
-The brain interprets the diverging rays by assuming they are coming from a point behind the lens, creating a virtual image.
What is the formula used to find the image distance (S') with a diverging lens?
-The formula used to find the image distance (S') with a diverging lens is S' = S * f / (s - f), where S is the distance to the object, f is the focal length, and s is the object distance from the lens.
What was the calculated image distance for the given example?
-The calculated image distance for the given example was -9.375 cm, indicating a virtual image in front of the lens.
Why is the image distance negative in the example?
-The image distance is negative because the image formed by a diverging lens is virtual and appears on the same side of the lens as the object.
What is the magnification formula for lenses?
-The magnification formula for lenses is magnification = -S' / s, where S' is the image distance and s is the object distance.
What was the magnification of the image in the example, and what does it indicate?
-The magnification of the image in the example was 0.625, which is 62.5% of the original object size, indicating the image is larger but still smaller than the object and upright.
How does the position of the object relative to the focal point affect the image with a diverging lens?
-With a diverging lens, whether the object is placed inside or outside the focal point, the image will always appear as a virtual image somewhere between the object and the lens.
What is the significance of the magnification being positive in the context of the example?
-A positive magnification indicates that the image is upright relative to the object.
What will be the focus of the next video, as mentioned in the script?
-The next video will focus on combinations of lenses, rather than a single lens, to demonstrate how the image is formed in such cases.
Outlines
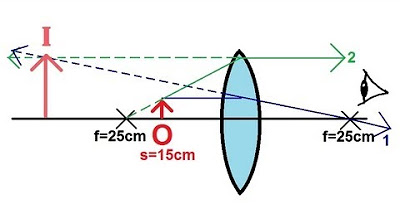
🔍 Understanding Diverging Lenses and Image Formation
This paragraph discusses the behavior of a diverging lens, specifically when an object is placed within the focal point, closer to the lens than the focal length. The focal length is given as -25 cm, indicating a negative focal length characteristic of diverging lenses. The explanation includes a step-by-step guide on drawing ray diagrams for a diverging lens, illustrating how rays diverge from the lens as if emanating from a focal point behind the lens. The observer perceives the rays as if they were coming from a virtual image formed between the object and the lens. The script then demonstrates how to calculate the exact location of the virtual image using the lens equation (S' = S * F / (S - F)), where S is the object distance, F is the focal length, and S' is the image distance. The calculation yields a virtual image at -9.375 cm from the lens, confirming its position in front of the lens. Additionally, the magnification is calculated to be 62.5% of the original object size, indicating an upright and smaller virtual image. The paragraph concludes by noting the consistency of image formation with a diverging lens, regardless of the object's position relative to the focal point.
Mindmap
Keywords
💡Diverging lens
💡Focal length
💡Ray diagram
💡Virtual image
💡Magnification
💡Object distance (S)
💡Image distance (S')
💡Lens formula
💡Parallel rays
💡Optical axis
Highlights
Introduction of a second example involving a diverging lens.
Explanation of the object being placed inside the focal point of a diverging lens.
Description of the negative focal length of the diverging lens, specifically -25 cm.
Ray diagrams for diverging lenses, starting with a line parallel to the optical axis.
Ray behavior after passing through the diverging lens, diverging as if emanating from the focal point.
Drawing the second ray from the object to the focal point and its divergence.
Observation of the rays diverging and not forming a real image behind the lens.
The brain's role in interpreting the apparent source of diverging rays to form a virtual image.
The consistency of image formation with a diverging lens regardless of object placement relative to the focal point.
Use of the lens equation to determine the exact location of the image.
Calculation of the image distance using the lens equation with given values.
Determination of the image being virtual and in front of the lens due to a negative value.
Explanation of magnification calculation and its significance in lens behavior.
Finding the magnification to be 62.5% of the original object, indicating the image is larger but still smaller than the object.
Observation that the image is upright due to the positive result of the magnification calculation.
Conclusion on the minimal difference in image formation when the object is placed at different distances from a diverging lens.
Anticipation of the next video involving combinations of lenses for further study.
Transcripts
Browse More Related Video
Physics - Optics: Lenses (1 of 2) Diverging Lens
Multiple Two Lens System with Diverging and Converging Lens
Physics - Optics: Lenses (3 of 4) Converging Lens
Physics - Optics: Lenses (1 of 4) Converging Lens
Physics - Optics: Lenses (4 of 4) Converging Lens
Physics - Optics: Lenses (3 of 5) Lens Combinations - Converging & Diverging Lenses
5.0 / 5 (0 votes)
Thanks for rating: