Physics - Optics: Lenses (3 of 4) Converging Lens

Michel van Biezen
30 Apr 201304:03
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script explores the behavior of a converging lens with a focal length of 25 cm when an object is placed 30 cm away. The script demonstrates the creation of a real, inverted, and enlarged image using the lens formula and explains the concept of magnification. As the object approaches the lens's focal point, the image distance increases, and the image size grows larger. The script also hints at what happens when the object is placed at and inside the focal point, promising further exploration in the next video.

Takeaways
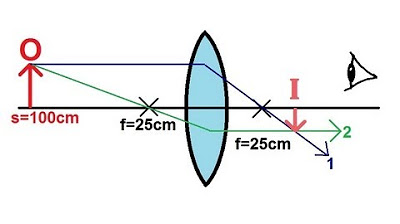
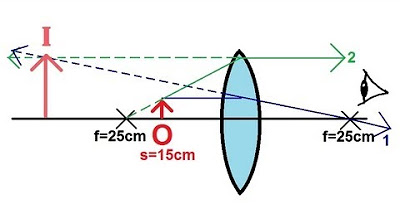
  • 🔍 The object is positioned 30 cm from a converging lens with a focal length of 25 cm.
  • 📏 Converging lenses have a positive focal length.
  • ➡️ The first ray travels from the top of the object to the lens and refracts through the focal point on the other side.
  • 🔄 The second ray goes from the top of the object through the focal point to the lens and refracts parallel to the principal axis.
  • 🔗 The rays converge on the other side of the lens, creating a real, inverted image.
  • 📐 The image distance (S') is calculated using the lens equation: S' = (S * F) / (S - F).
  • 💡 The calculation for S' is 30 * 25 / (30 - 25), resulting in 150 cm, meaning the image is 150 cm behind the lens.
  • 🔍 The magnification (M) is found using the formula: M = -S' / S. In this case, it's -150 / 30, resulting in a magnification of -5.
  • 🔄 A magnification of -5 means the image is five times larger than the object and inverted.
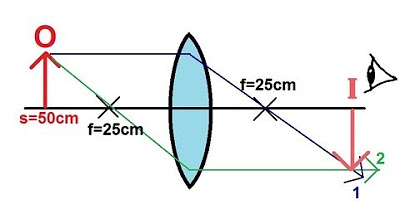
  • 🔍 As the object moves closer to the focal point, the image moves farther from the lens and becomes larger.
Q & A

  • What type of lenses are being discussed in the script?

    -The script discusses converging lenses, which have a positive focal length and cause light to converge at a point.

  • What is the focal length of the lens mentioned in the script?

    -The focal length of the lens mentioned in the script is 25 cm.

  • What happens when an object is placed at a distance of 30 cm from the lens?

    -When the object is placed at a distance of 30 cm from the lens, the rays of light refract through the lens and converge to form a real image on the other side.

  • How is the first ray in the ray diagram defined in the script?

    -The first ray in the ray diagram is defined as coming from the top of the object, passing through the lens, and continuing on through the focal point on the other side.

  • What is the second ray in the ray diagram, and how does it behave?

    -The second ray is from the tip of the object to the focal point, then to the lens where it refracts and continues on parallel to the normal, indicating the direction of the refracted ray.

  • What is the equation used to find the image distance in the script?

    -The equation used to find the image distance is \( S' = \frac{SF}{s - F} \), where \( S \) is the object distance, \( S' \) is the image distance, and \( F \) is the focal length of the lens.

  • What was the calculated image distance when the object was 30 cm away from the lens?

    -The calculated image distance was initially stated as -150 cm, but the script corrected this to a positive value, indicating an error in the calculation.

  • What does a positive image distance indicate about the image formed by the lens?

    -A positive image distance indicates that the image is real, formed on the opposite side of the lens from the object, and is inverted.

  • What is the relationship between the object distance and the image distance as the object gets closer to the lens?

    -As the object gets closer to the lens, the image moves farther away from the lens and becomes larger.

  • What is the formula for calculating magnification in the script?

    -The formula for calculating magnification in the script is \( m = -\frac{S'}{s} \), where \( S' \) is the image distance and \( s \) is the object distance.

  • What does the magnification of -5 mean in the context of the script?

    -A magnification of -5 means the image is five times larger than the object and is inverted.

  • What happens to the image when the object is placed at the focal point of the lens?

    -When the object is placed at the focal point, the image will theoretically become infinitely far away and infinitely large, though this is not practically observable.

  • What will be the subject of the next video in the series?

    -The next video will discuss what happens when the object is placed inside the focal point of the lens.

Outlines
00:00
🔍 Understanding Converging Lenses: Moving Objects Closer

In this section, we explore the behavior of converging lenses as the object moves closer to the lens. With an object distance of 30 cm and a focal length of 25 cm, we draw a ray diagram. The first ray travels from the top of the object through the lens and continues through the focal point. The second ray moves from the tip of the object to the focal point, then bends and travels parallel to the normal. These rays converge to form a real, inverted image on the other side of the lens. Calculations show the image distance (S') to be 150 cm. Magnification is calculated as -5, indicating the image is five times larger and inverted.

🧮 Calculating Image Distance and Magnification

Using the lens equation S' = SF / (S - F), we find the image distance to be 150 cm behind the lens, confirming it is a real image. An error correction reveals the correct interpretation of the image distance as positive. The magnification is determined to be -5, signifying the image is five times the object's size and inverted. This section emphasizes the relationship between object distance, image distance, and magnification for converging lenses.

📏 Relationship Between Object Distance and Image Formation

As the object moves closer to the focal point, the image moves further away from the lens and becomes larger. When the object reaches the focal point, the image distance becomes infinitely large. This theoretical discussion prepares us for the next scenario where the object is placed inside the focal point, which will be covered in the subsequent video.

Mindmap
Keywords
💡Converging Lens
A converging lens is a type of lens that focuses incoming parallel rays of light to a single point, known as the focal point. In the video script, the converging lens is described as having a positive focal length of 25 cm, which means it bends the light rays towards the optical axis. The concept of a converging lens is central to understanding how real images are formed, as described in the script when the object is placed at a distance of 30 cm from the lens, and the light rays converge on the other side, forming a real image.
💡Focal Length
The focal length is the distance between the center of a lens and its focal point, where parallel light rays converge or appear to diverge. In the script, the focal length is given as 25 cm, which is a positive value for the converging lens discussed. The focal length determines how strongly the lens converges or diverges light and plays a crucial role in the calculations of image formation, such as using the lens formula to find the image distance. The script illustrates how the focal length is a key parameter in the equation used to calculate the image's position.
💡Ray Diagram
A ray diagram is a graphical method used to determine the path of light through optical systems, like lenses and mirrors, and to locate the position of images formed by these systems. In the video, the ray diagram is used to demonstrate how light rays travel through a converging lens and form an image. The script outlines the steps to draw the ray diagram: one ray travels parallel to the principal axis and passes through the focal point after refraction, while another passes through the lens's focal point and refracts parallel to the axis. The intersection of these rays on the other side of the lens indicates the formation of a real image.
💡Object Distance (s)
Object distance, denoted as 's' in optics, refers to the distance between the object and the lens. In the script, the object distance is 30 cm, which is an important parameter for determining where the image will form. The object distance is used in the lens equation, S' = SF/(S - F), to find the image distance. As the object moves closer to the lens, the image distance increases, demonstrating how object distance affects image formation. This concept is key in understanding the relationship between the object's position and the characteristics of the image, such as size and orientation.
💡Image Distance (S')
Image distance, represented as 'S' prime (S'), is the distance between the lens and the image formed by it. According to the script, the image distance is calculated using the formula S' = SF/(S - F), yielding a positive 150 cm. This positive value indicates that the image is real and located on the opposite side of the lens from the object. Image distance helps determine whether the image is real or virtual and its size and orientation. In this scenario, the real image is larger and inverted, and the script emphasizes how changing the object distance affects the image distance and, consequently, the image characteristics.
💡Real Image
A real image is an image formed when light rays converge at a point after passing through a lens or reflecting off a mirror. It can be projected onto a screen because it is created by actual light rays converging at the image location. The script mentions a real image when the rays meet on the other side of the converging lens, indicating that the image is inverted and located at 150 cm. Real images are essential in optics as they differ from virtual images, which cannot be projected and are formed where rays appear to diverge. The concept of a real image highlights how lenses can create tangible projections that can be observed on a screen.
💡Inverted Image
An inverted image is one that appears upside down relative to the object's orientation. This occurs when light rays cross after passing through a lens or reflecting off a mirror. In the video script, the image formed is described as inverted because it appears upside down relative to the object. The negative magnification value confirms this inversion. Understanding inverted images is crucial in optics, as it explains how lenses and mirrors affect the orientation of images, which is an important consideration in designing optical devices like cameras and microscopes.
💡Magnification
Magnification is a measure of how much larger or smaller an image appears compared to the actual object. It is calculated as the ratio of the image distance (S') to the object distance (s), often denoted as 'm.' In the script, magnification is calculated as -S'/s, resulting in a value of -5, indicating that the image is five times larger than the object and inverted. Magnification provides insight into the size and orientation of the image, making it a key factor in understanding how lenses and optical systems alter the perceived size of objects.
💡Principal Axis
The principal axis is the straight line that passes through the center of a lens and its two focal points. It serves as a reference line for drawing ray diagrams and analyzing the paths of light rays through optical systems. In the video script, the principal axis is implied when discussing the parallel and converging rays, which are drawn relative to this axis. The principal axis is crucial for understanding how lenses focus light and form images, providing a framework for constructing ray diagrams and predicting the behavior of light in optical systems.
💡Lens Equation
The lens equation is a mathematical formula that relates the object distance (s), image distance (S'), and focal length (f) of a lens. It is often expressed as 1/S' + 1/s = 1/f, but in the script, a rearranged version S' = SF/(S - F) is used. This equation is fundamental in optics as it allows for calculating the position of an image formed by a lens, given the object distance and focal length. In the script, the lens equation is applied to determine the image distance and understand how the lens focuses light to create a real image.
Highlights

Exploring the behavior of thin converging lenses with positive focal lengths.

Demonstration of how moving an object closer to the lens affects image formation.

Object placed at a distance of 30 cm from a lens with a 25 cm focal length.

Ray diagram illustrating the refraction of light through the lens to form a real image.

Use of lens formula S' = (S * F) / (S - F) to calculate image distance.

Calculation error correction in the lens formula application.

Determination that the image is real and located 150 cm behind the lens.

Observation that as the object approaches the focal point, the image moves farther away and becomes larger.

Introduction of magnification formula m = -S' / S to find the size and orientation of the image.

Calculation of the magnification showing the image is 5 times larger than the object and inverted.

Explanation of the relationship between object distance, image distance, and magnification.

Theoretical prediction of image characteristics when the object is at the focal point.

Anticipation of what happens when the object is placed inside the focal point in the next video.

Teaching the concept of real images formed by converging lenses and their properties.

Visual representation of the movement and size change of the image as the object's distance changes.

Emphasizing the practical applications of lens equations in real-world scenarios.

Engaging the audience with a promise of further exploration in the next video installment.

Transcripts

Browse More Related Video

Physics - Optics: Lenses (1 of 4) Converging Lens

Physics - Optics: Lenses (2 of 4) Converging Lens

Physics 54 Optics: Mirrors (2 of 6) Concave Mirror

Physics - Optics: Lenses (2 of 2) Diverging Lens

Physics - Optics: Lenses (1 of 2) Diverging Lens

Physics - Optics: Lenses (4 of 4) Converging Lens

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Lens OpticsConverging LensImage FormationFocal LengthRay DiagramObject DistanceImage DistanceMagnificationInverted ImageOptics Tutorial