Physics - Optics: Lenses (1 of 5) Lens Combinations - Two Converging Lenses

Michel van Biezen
30 Apr 201311:55
EducationalLearning
32 Likes 10 Comments

TLDRThis lecture script delves into solving a double lens problem in optics. It guides through the process of finding the final image formed by an object through two converging lenses with focal lengths of 30 cm and 20 cm. The method involves calculating the first image as if only one lens exists, then using that image as the object for the second lens. The script explains the equations for image distance and magnification, revealing that the final image is real, inverted, and one-third the size of the original object, providing a clear step-by-step approach to double lens problems.

Takeaways
  • 🔍 The problem involves a combination of two converging lenses with focal lengths of 30 cm and 20 cm.
  • 📐 The first step is to draw a ray diagram for the image formed by the first lens, ignoring the second lens.
  • 🎯 Two main rays are used in the diagram: one that passes through the focal point and another that is parallel to the principal axis.
  • 🌌 The first image (Image 1) is found to be real and inverted, located at 75 cm from the first lens.
  • 🔢 The magnification of Image 1 is -1.5 times the size of the object, indicating it's larger and inverted.
  • 🔄 Image 1 then acts as the object for the second lens, with a new object distance of -65 cm.
  • 📏 The second image (Image 2) is calculated to be real, located 15.3 cm behind the second lens.
  • 🔄 The magnification of Image 2 relative to Image 1 is +0.235, meaning it's smaller and in the same orientation as Image 1.
  • 🔗 The total magnification from the original object to Image 2 is -0.35, which is inverted and one-third the size of the original object.
  • 📚 The process involves using the lens equation for each lens separately and considering the first image as the second object.
  • 📉 Understanding the direction of rays after passing through the second lens can be challenging, but the equations provide accurate values.
Q & A

  • What is the purpose of the lecture?

    -The purpose of the lecture is to solve a combination lens problem involving two converging lenses with different focal lengths to find the final image formed by the object due to the lenses.

  • What are the focal lengths of the two lenses mentioned in the script?

    -The first lens has a focal length of 30 centimeters, and the second lens has a focal length of 20 centimeters.

  • What is the first step in solving the lens problem as described in the script?

    -The first step is to draw the ray diagram for the image formed by the first lens, ignoring the presence of the second lens.

  • How many rays are used to draw the ray diagram for the first lens?

    -Two rays are used to draw the ray diagram for the first lens: one that passes through the focal point and another that is parallel to the principal axis.

  • What is the formula used to find the image distance (s') for the first lens?

    -The formula used to find the image distance for the first lens is \( s' = \frac{s \cdot F_1}{s - F_1} \), where \( s \) is the object distance, \( F_1 \) is the focal length of the first lens, and \( s' \) is the image distance.

  • What does a positive image distance (s') indicate about the image formed by the first lens?

    -A positive image distance indicates that the image formed by the first lens is real, inverted, and located to the right of the lens.

  • How is the image formed by the first lens used in the calculation for the second lens?

    -The image formed by the first lens acts as the object for the second lens, and its distance from the second lens is used as the new object distance in the calculation.

  • What is the formula used to find the image distance for the second lens?

    -The formula used to find the image distance for the second lens is \( s'_2 = \frac{s_2 \cdot F_2}{s_2 - F_2} \), where \( s_2 \) is the object distance for the second lens (which is the image distance from the first lens), \( F_2 \) is the focal length of the second lens, and \( s'_2 \) is the image distance for the second lens.

  • What does a negative object distance for the second lens calculation imply about the object's position?

    -A negative object distance for the second lens calculation implies that the object (in this case, the image from the first lens) is located to the left of the second lens, behind it.

  • How is the total magnification of the system calculated?

    -The total magnification of the system is calculated by multiplying the magnifications of each lens (M1 and M2), where M1 is the magnification of the first image relative to the object, and M2 is the magnification of the second image relative to the first image.

  • What does a negative total magnification indicate about the final image?

    -A negative total magnification indicates that the final image is inverted relative to the original object.

Outlines
00:00
🔍 Understanding Lens Image Formation

This paragraph introduces a problem involving two converging lenses with different focal lengths, aiming to find the final image formed by the object through both lenses. The process begins with drawing a ray diagram using only the first lens, ignoring the second lens's presence. The first ray is drawn from the object's top to the first lens, diverging through the focal point. A second ray is drawn through the focal point in front of the lens and continues parallel after hitting the lens, meeting the first ray to form the first image. The paragraph explains how the second lens affects the rays, bending them further and moving the image's location, which will be determined using lens equations.

05:02
🔢 Calculating Image Positions and Magnifications

The paragraph calculates the first image's position using lens equations, resulting in a real image 75 centimeters from the first lens with a magnification of -1.5, indicating an inverted image. It proceeds to find the second image by considering the first image as the object for the second lens. The object distance for the second lens is 65 centimeters, negative because it's behind the lens. Using lens equations again, the second image is found to be real, 15.3 centimeters from the second lens. The magnification of the second image is 0.235, meaning it's smaller and in the same orientation as the first image. The total magnification is -0.35, indicating the final image is inverted relative to the original object.

10:03
🔄 Summary of Double Lens Problem Solving

This paragraph summarizes the steps for solving double lens problems: first, find the image formed by the first lens while ignoring the second lens. The first image acts as the object for the second lens, using the object distance calculated as negative because it's behind the lens. The image distance for the second lens is calculated, showing it's real and upright relative to the object (first image). The total magnification is obtained by multiplying the magnifications from both lenses, resulting in an inverted image smaller than the original object. The challenges of accurately predicting ray directions after passing through the second lens are noted, but equations provide precise values.

Mindmap
Keywords
💡Converging lens
A converging lens, also known as a convex lens, focuses incoming light rays to a point. In the video, two converging lenses with focal lengths of 30 cm and 20 cm are used to demonstrate how to find the final image formed by a combination of lenses. These lenses are crucial in creating the intermediate and final images.
💡Focal length
Focal length is the distance from the center of a lens to its focal point, where light rays converge. The video involves two lenses with focal lengths of 30 cm and 20 cm, which determine how each lens bends light rays to form images. The focal length is essential for calculating image positions and magnifications.
💡Ray diagram
A ray diagram is a graphical method used to determine the path of light rays through optical systems. In the video, ray diagrams are drawn to trace the path of light rays from the object through each lens, helping to visualize and calculate the positions of the images formed by the lenses.
💡Image distance (s')
Image distance (s') is the distance between the lens and the image it forms. The video calculates the image distances for both lenses, showing that the first image (s1') is formed at 75 cm from the first lens, and the second image (s2') is formed at 15.3 cm from the second lens. These distances are essential for understanding where the images appear relative to the lenses.
💡Object distance (s)
Object distance (s) is the distance between the object and the lens. In the video, the initial object distance is 50 cm for the first lens. For the second lens, the object distance becomes the distance between the first image and the second lens, adjusted for the distance between the lenses. This concept is key for setting up the calculations for image formation.
💡Magnification (M)
Magnification (M) is the ratio of the height of the image to the height of the object. It indicates how much larger or smaller the image is compared to the object. The video calculates magnifications for both lenses, showing that the first image is inverted and 1.5 times larger than the object, while the second image is 23.5% the size of the first image. Magnification helps understand the size and orientation changes through the lens system.
💡Real image
A real image is formed when light rays converge and can be projected onto a screen. In the video, both the first and second images are real images, as indicated by their positive image distances. Real images are crucial in optical systems because they represent actual points where light rays meet.
💡Inverted image
An inverted image is one that is upside down relative to the object. In the video, the first image formed by the first lens is inverted, as indicated by the negative magnification. Understanding image inversion is important for predicting the orientation of images formed by lenses.
💡Lens equation
The lens equation (1/f = 1/s + 1/s') relates the focal length (f), object distance (s), and image distance (s'). In the video, this equation is used to calculate the image distances for both lenses, helping to determine where the images are formed. The lens equation is fundamental in optics for solving image formation problems.
💡Intermediate image
An intermediate image is the image formed by the first lens, which then acts as the object for the second lens. In the video, the intermediate image is formed 75 cm from the first lens and 65 cm behind the second lens. Understanding intermediate images is crucial for analyzing multi-lens systems.
Highlights

Introduction to a combination lens problem involving two converging lenses with focal lengths of 30 cm and 20 cm.

First step: draw the ray diagram for the image formed by the first lens, ignoring the presence of the second lens.

Explanation of the ray diagram for the first lens, showing how rays change direction and meet at the focal point.

Identification of the first image formed by the first lens, labeled as image 1.

Analysis of the effect of the second lens on the rays coming from the first image.

Using the lens equation to find the exact position and magnification of the first image.

Calculation of the first image distance (s1 prime) as 75 cm, indicating a real, inverted image.

Magnification of the first image (M1) calculated as -1.5, indicating it is 1.5 times the size of the object and inverted.

Image 1 acts as the object for the second lens, with an adjusted object distance for the second lens calculation.

Calculation of the second object distance (s2) as -65 cm, indicating it is behind the second lens.

Using the lens equation to find the second image distance (s2 prime) as 15.3 cm, indicating a real image.

Magnification of the second image (M2) calculated as 0.235, indicating it is 23.5% the size of the first image and retains the same orientation.

Total magnification of the final image relative to the original object calculated as -0.35, indicating the final image is inverted and one-third the size of the original object.

Summary of the process: solving a double lens problem by analyzing each lens separately and combining the results.

Final review emphasizing the use of equations to find real values and the challenge of predicting ray directions after the second lens.

Transcripts

Browse More Related Video

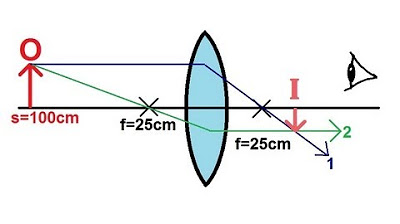
Physics - Optics: Lenses (1 of 4) Converging Lens

Physics - Optics: Lenses (4 of 5) Lens Combinations - Converging & Diverging Lenses

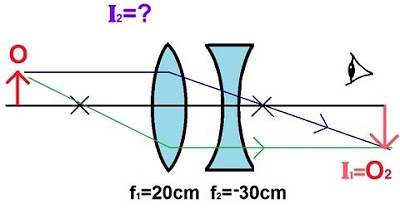
Physics - Optics: Lenses (3 of 5) Lens Combinations - Converging & Diverging Lenses

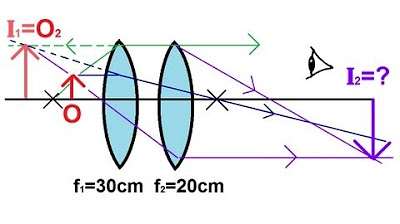
Physics - Optics: Lenses (2 of 5) Lens Combinations - Two Converging Lenses

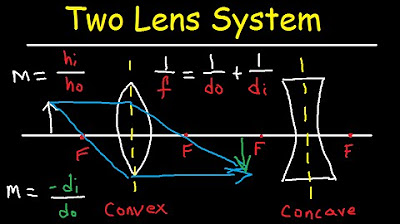
Multiple Two Lens System with Diverging and Converging Lens

Physics - Optics: Lenses (3 of 4) Converging Lens

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Optics LectureDouble LensImaging ProblemFocal LengthRay DiagramConverging LensesImage FormationMagnificationEducational ContentPhysics Tutorial