Physics 54 Optics: Mirrors (3 of 6) Concave Mirror
TLDRThis script explains the process of finding the image of an object placed in front of a concave mirror with a focal length of 25 cm. Using a graphical method, it demonstrates how rays reflect to form a virtual image. The image is calculated to be 37.5 cm behind the mirror, 2.5 times larger than the object, and upright. The explanation clarifies the concept of virtual images and how the human brain interprets the reflected rays.
Takeaways
- 🔍 The script discusses finding the image formed by a concave mirror when an object is placed in front of it.
- 🌀 The concave mirror has a positive focal length of 25 centimeters, indicating the distance from the mirror to the focal point.
- 📏 The distance from the mirror to the center of curvature is twice the focal length, which is 50 centimeters in this case.
- 🏷 The object is placed 15 centimeters away from the mirror, which is between the mirror and the focal point.
- 📐 The image is determined using a graphical method involving the reflection of rays from the object to the mirror.
- 👀 An observer's perspective is considered, as they see the reflected rays and interpret them as coming from a single point.
- 📉 The script describes a problem with the graphical method where the rays seem to diverge and not meet to form a clear image.
- 🧠 The human brain interprets the diverging rays as if they originate from a virtual image behind the mirror.
- ✏️ Mathematically, the image distance (s') is calculated using the formula s' = (SF) / (S - F), where S is the object distance and F is the focal length.
- 🔢 The calculated image distance is -37.5 centimeters, indicating that the image is virtual and appears 37.5 centimeters behind the mirror.
- 🔄 The magnification (M) is found to be 2.5, meaning the image is 2.5 times larger than the object and is upright.
Q & A
What type of mirror is being discussed in the script?
-The script discusses a concave mirror.
What is the focal length of the concave mirror mentioned in the script?
-The focal length of the concave mirror is 25 centimeters.
What is the distance from the mirror to the center of curvature for the given concave mirror?
-The distance from the mirror to the center of curvature is 50 centimeters.
Where is the object placed in relation to the concave mirror?
-The object is placed 15 centimeters away from the mirror, which is closer to the mirror than the focal point.
What is the graphical method used to find the image formed by the concave mirror?
-The graphical method involves drawing rays from the object to the mirror and reflecting them according to the mirror's properties, then finding the point where the reflected rays appear to diverge from.
Why does the second ray drawn from the object through the focal point require a dotted line?
-A dotted line is used because the object is already past the focal point, so the ray is extended from the focal point to the object and then reflected parallel to the normal.
What does the observer see when looking at the mirror, and how does this contribute to the formation of the image?
-The observer sees rays that appear to come from a single point, which the brain interprets as an image, even though the rays are diverging.
Is the image formed by the concave mirror in the script real or virtual?
-The image formed is virtual, as it appears to be behind the mirror and is not physically present there.
What mathematical formula is used to find the position of the image (s') in relation to the mirror?
-The formula used is s' = (SF / (s - F)), where s is the object distance, F is the focal length, and s' is the image distance.
What is the magnification of the image formed by the concave mirror, and what does the sign of the magnification indicate?
-The magnification is 2.5 times the size of the object, and the positive sign indicates that the image is upright.
What does the negative value of the image distance (s') signify in the context of the script?
-A negative value for the image distance indicates that the image is virtual and appears to be on the same side of the mirror as the object.
Outlines
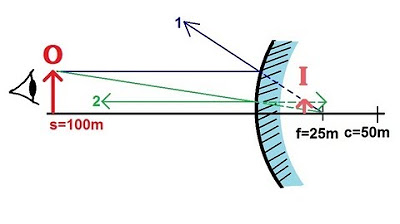
🔍 Finding the Image with a Concave Mirror
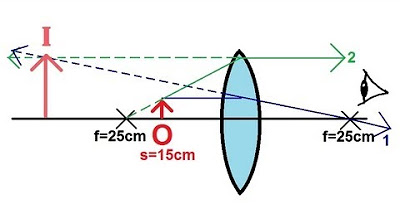
This paragraph explains the process of determining the image formed by a concave mirror when an object is placed in front of it. The mirror has a positive focal length of 25 centimeters, meaning the distance from the mirror to the focal point is 25 centimeters, and the distance to the center of curvature is 50 centimeters. The object is placed 15 centimeters from the mirror, closer to the mirror than the focal point. The explanation uses a graphical method to trace two rays of light: one parallel to the normal reflected through the focal point, and the other from the object through the focal point to the mirror. The rays are extrapolated to form a virtual image behind the mirror, which is not physically present but appears to be due to the brain's interpretation of the light rays. The mathematical formula to find the image distance (s') and magnification (M) is also provided, with the example yielding an image 37.5 centimeters behind the mirror, 2.5 times larger than the object, and upright.
Mindmap
Keywords
💡Concave Mirror
💡Focal Length
💡Center of Curvature
💡Object Distance
💡Graphical Method
💡Normal
💡Observer
💡Virtual Image
💡Magnification
💡Upright Image
Highlights
Concave mirrors have positive focal lengths, with the example having a focal length of 25 centimeters.
The distance from the mirror to the center of curvature is 50 centimeters.
The object is placed 15 centimeters away from the mirror, closer to the mirror than the focal point.
A graphical method is used to find the image formed by the concave mirror.
The first ray is drawn parallel to the normal until it hits the mirror and reflects through the focal point.
An observer is represented by a light ball looking into the mirror.
The second ray is drawn from the object through the focal point to the mirror.
A dotted line is used when the ray passes the focal point before hitting the mirror.
The second ray reflects parallel to the normal after hitting the mirror.
The brain interprets the diverging rays as coming from a single point, forming a virtual image.
The image appears behind the mirror, indicating it is a virtual image.
The image distance s' is calculated using the formula s' = -F / (s - F).
The image is found to be 37.5 centimeters behind the mirror, confirming it is virtual.
The magnification M is calculated as M = -s' / s, resulting in a positive value of 2.5.
The positive magnification value indicates the image is upright and 2.5 times the size of the object.
The problem demonstrates the process of finding the image formed by a concave mirror using graphical and mathematical methods.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: