Physics 51/54 - Optics: Mirrors (6 of 6) Flat Mirror

Michel van Biezen
30 Apr 201304:53
EducationalLearning
32 Likes 10 Comments

TLDRThis educational script explains the properties and behavior of flat mirrors, focusing on their unique characteristic of having an infinite focal length. It demonstrates how rays of light reflect off a flat mirror, resulting in a virtual image that appears to be the same distance behind the mirror as the object is in front. The script also illustrates the process of finding the image distance and magnification, revealing that the image formed by a flat mirror is upright and the same size as the object, thereby providing a clear understanding of the concept.

Takeaways
  • πŸ” The focal length of a flat mirror is considered to be infinity, meaning the focal point is infinitely far away.
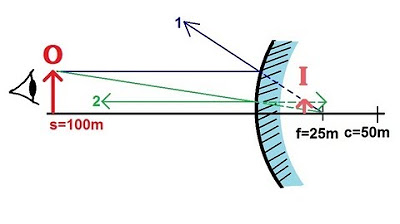
  • πŸ“ To find the focal point of a concave mirror, shine light parallel to the normal, and the reflected rays will converge at a point, which is the focal point.
  • πŸ”„ For a flat mirror, the reflected rays will go back in the direction they came from, never converging unless considered infinitely far away.
  • πŸ‘€ The human brain perceives an image formed by a flat mirror where the reflected rays appear to diverge from, even though they do not actually converge.
  • 🎯 The image formed by a flat mirror is virtual, meaning it appears to be behind the mirror and cannot be projected onto a screen.
  • βœ‚οΈ The image distance (S') can be calculated using the formula S' = -SF/(S - F), with the focal length (F) being infinity for a flat mirror.
  • πŸ”’ In the given example, the object is placed 50 cm away from the mirror, and the image distance is found to be -50 cm, indicating a virtual image behind the mirror.
  • 🌐 The magnification (M) of a flat mirror is calculated as M = -S'/S, and in this case, it equals 1, meaning the image is the same size as the object.
  • πŸ“ The magnification of 1 also indicates that the image is upright, as there is no inversion in size or orientation.
  • πŸ€– Understanding the properties of flat mirrors is essential for analyzing and solving problems related to reflection and image formation.
  • πŸ“š The script provides a step-by-step explanation of how to work with flat mirrors, including determining image distance, magnification, and orientation.
Q & A

  • What is the focal length of a flat mirror?

    -The focal length of a flat mirror is considered to be infinite, meaning the focal point is infinitely far away.

  • How does the focal point of a flat mirror differ from that of a concave mirror?

    -In a concave mirror, parallel rays reflect back through a focal point, whereas in a flat mirror, the rays reflect back in the same direction they came from, implying the focal point is infinitely far away.

  • Why do we use the term 'infinity' for the focal length of a flat mirror?

    -We use 'infinity' for the focal length of a flat mirror because the reflected rays do not converge at a finite point; they would only converge at an infinitely far distance.

  • How does the brain perceive the image formed by a flat mirror?

    -The brain perceives the image by interpreting the reflected rays as if they came from a point behind the mirror where they appear to converge, creating a virtual image.

  • What type of image does a flat mirror produce?

    -A flat mirror produces a virtual image, which appears to be behind the mirror rather than in front of it.

  • How can you determine the image distance for an object in front of a flat mirror?

    -You can use the equation S' = -SF / (s - F), where S is the object distance, F is the focal length, and S' is the image distance. For a flat mirror, F is infinity, so the image distance is the same as the object distance but with a negative sign, placing it behind the mirror.

  • What is the magnification of an image formed by a flat mirror?

    -The magnification of an image formed by a flat mirror is 1, meaning the image is the same size as the object.

  • Is the image formed by a flat mirror upright or inverted?

    -The image formed by a flat mirror is upright, as the magnification is 1 and there is no flipping of the image vertically or horizontally.

  • What happens when you draw a ray from the object to the mirror at the point where the normal hits the mirror?

    -According to the reflection laws of mirrors, the angle of incidence is equal to the angle of reflection, and the ray will be reflected in a direction that maintains this relationship.

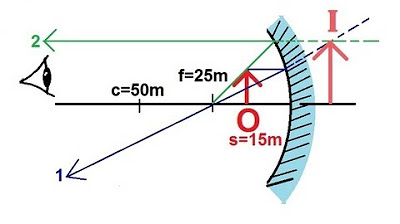
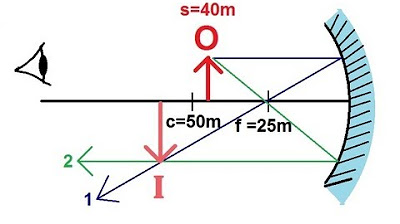
  • How can you graphically find the image for an object in front of a flat mirror?

    -You draw rays from the object to the mirror, reflecting them according to the law of reflection, and then use the brain's interpretation of where these rays appear to converge to locate the virtual image.

  • What is the significance of the negative sign in the image distance calculation for a flat mirror?

    -The negative sign indicates that the image is virtual and located on the same side of the mirror as the object but behind the mirror's surface.

Outlines
00:00
πŸͺž Understanding Flat Mirrors and Their Image Formation

This paragraph explains the concept of flat mirrors, emphasizing that their focal length is considered infinite, meaning the focal point is infinitely far away. It illustrates the behavior of light rays reflecting off a flat mirror, showing that they return in the direction from which they came, never converging to form a real image. The explanation includes a practical method to determine the focal point using parallel light rays. The paragraph then graphically demonstrates how the human brain perceives a virtual image behind the mirror by interpreting the paths of reflected rays. It concludes with a mathematical approach to calculate the image distance for a flat mirror, which turns out to be the same as the object distance but on the opposite side of the mirror, indicating a virtual image. The magnification is also discussed, revealing that it remains the same as the object size, and the image is upright.

Mindmap
Keywords
πŸ’‘Flat Mirror
A flat mirror is a type of mirror with a smooth surface that reflects light without distorting the image. In the video, the concept of a flat mirror is central to understanding how the reflection of light occurs and how it forms an image. The script explains that unlike curved mirrors, a flat mirror does not have a focal point because the light rays reflect back in the same direction from which they came, indicating an infinitely far focal point.
πŸ’‘Focal Length
Focal length is the distance from the optical center of a lens or mirror to the point where parallel rays of light converge or appear to diverge from. In the context of the video, it's mentioned that for a flat mirror, the focal length is considered to be infinite, as the reflected rays do not converge at a finite point but rather extend indefinitely, which is a key aspect in understanding the behavior of light with flat mirrors.
πŸ’‘Object Distance
Object distance refers to the distance between the object being viewed and the mirror. In the script, the object is placed 50 cm away from the mirror, which is a critical piece of information for calculating the image distance and understanding how the image is formed relative to the object's position.
πŸ’‘Image Distance
Image distance is the distance from the mirror to the point where the image appears to be. The script explains that for a flat mirror, the image distance is the same as the object distance but on the opposite side of the mirror, which is a virtual distance, indicating that the image is not formed on a physical surface but appears to be located behind the mirror.
πŸ’‘Virtual Image
A virtual image is an image that appears to be located behind the mirror and cannot be projected onto a screen. The video script describes how the brain perceives the convergence of reflected rays and forms an image, even though the rays do not actually meet, resulting in a virtual image that is upright and the same size as the object.
πŸ’‘Magnification
Magnification in optics refers to the ratio of the size of the image to the size of the object. The script explains that with a flat mirror, the magnification is 1, meaning the image is the same size as the object. This is a fundamental concept in understanding how flat mirrors produce images without altering their size.
πŸ’‘Upright Image
An upright image is one that appears the same way as the object, without being inverted. The video script emphasizes that the image formed by a flat mirror is upright, which is an important characteristic of flat mirror reflections and contrasts with the behavior of some curved mirrors.
πŸ’‘Reflection Laws
Reflection laws are the principles that govern how light rays reflect off a surface. The script mentions that the angle of incidence (the angle at which a ray of light strikes a surface) is equal to the angle of reflection (the angle at which the ray leaves the surface), which is a fundamental law of reflection used to explain how images are formed by mirrors.
πŸ’‘Concave Mirror
A concave mirror is a type of curved mirror that bends light inward and can focus parallel rays of light at a focal point. The script contrasts the behavior of a concave mirror with that of a flat mirror, explaining how rays parallel to the normal of a concave mirror will reflect and converge at a focal point, unlike the behavior of a flat mirror.
πŸ’‘Normal
The normal is a line perpendicular to the surface at the point of incidence. In the script, the normal is used to describe the path of light rays as they interact with the mirror, with the angle of incidence being measured relative to the normal. This concept is crucial for understanding the reflection of light and the formation of images.
πŸ’‘Theta Subscript i
Theta sub i (ΞΈ_i) represents the angle of incidence, which is the angle between the incoming light ray and the normal to the surface. The script uses this term to describe the relationship between the angle of incidence and the angle of reflection, emphasizing the law of reflection for mirrors.
Highlights

Introduction to the example of a flat mirror and its properties.

Explanation of the focal length of a flat mirror being equal to infinity.

Demonstration of how rays reflect off a concave mirror to its focal point.

Description of the process to find the focal point of a mirror using parallel light rays.

Difference between a flat mirror and a concave mirror regarding focal points and convergence of rays.

Graphical method to find the image in a flat mirror using reflection laws.

Observation that the image formed by a flat mirror is virtual and appears behind the mirror.

Use of the equation S' = SF / (s - F) to calculate image distance in a flat mirror.

Simplification of the equation due to the focal length being infinity, leading to an image distance of -50 cm.

Confirmation that the image is virtual due to its position behind the mirror.

Calculation of magnification (M) using the formula M = -S' / s, resulting in a magnification of one.

Conclusion that the image size is the same as the object size due to the magnification of one.

Observation that the image is upright, indicated by a positive magnification value.

Summary of the properties of flat mirrors: virtual image, same size as the object, and upright orientation.

Explanation of how the brain perceives the convergence of rays to form a virtual image.

Final remarks on working with flat mirrors and understanding their optical behavior.

Transcripts

Browse More Related Video

Physics 54 Optics: Mirrors (4 of 6) Convex Mirror

Physics 54 Optics: Mirrors (3 of 6) Concave Mirror

Physics 54 Optics: Mirrors (2 of 6) Concave Mirror

Ray Diagrams

Concave Mirrors and Convex Mirrors Ray Diagram - Equations / Formulas & Practice Problems

Physics - Optics: Lenses (2 of 2) Diverging Lens

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Flat MirrorsImage FormationMagnificationOpticsPhysicsEducationalReflection LawsVirtual ImageUpright ImageInfinite Focal Length