Physics 54 Optics: Mirrors (2 of 6) Concave Mirror

Michel van Biezen
29 Apr 201303:34
EducationalLearning
32 Likes 10 Comments

TLDRThis educational script demonstrates the principles of image formation by a concave mirror with a 25 cm focal length. The object is placed between the focal point and the center of curvature, leading to a real, inverted image. Using graphical and mathematical methods, the image distance is calculated to be approximately 66.7 cm, with a magnification of 1.67 times the object size, indicating the image is larger and inverted. The script effectively explains the process of finding the image properties when the object is positioned at different distances from the mirror.

Takeaways
  • 🔍 The example is about a concave mirror with a positive focal length of 25 cm, indicating the distance from the lens to the focal point.
  • 🌀 The center of curvature is twice the focal length, which is 50 cm in this case.
  • 📍 The object is placed between the center of curvature and the focal point, unlike the previous example where the object was placed farther away.
  • 📏 Graphical method is used first to approximate the location of the image by drawing rays parallel to the normal and through the focal point.
  • 🖼️ The image is found to be farther than the center of curvature, suggesting a real image.
  • 📘 Mathematical formula is then applied to find the exact location of the image, using the equation S' = SF / (s - f).
  • ✂️ The object distance (s) is given as 40 cm, and the focal length (f) is 25 cm, which is used in the formula.
  • 🔢 The calculated image distance (S') is approximately 66.7 cm, confirming the image is real and located beyond the mirror.
  • 🔄 Magnification is determined using the formula M = -S' / s, resulting in a value of 1.67, indicating the image is larger than the object.
  • 🔁 The negative sign in the magnification indicates that the image is inverted, or upside down.
  • 🔄 The process demonstrates how to find the image of an object placed in front of a concave mirror when the object is between the center of curvature and the focal point.
Q & A

  • What type of mirror is being discussed in the script?

    -The script discusses a concave mirror.

  • What is the focal length of the concave mirror mentioned in the script?

    -The focal length of the concave mirror is 25 cm.

  • What is the relationship between the focal length and the distance from the lens to the center of curvature?

    -The distance from the lens to the center of curvature is twice the focal length, which in this case is 50 cm.

  • Where is the object placed in relation to the mirror in the example?

    -The object is placed between the center of curvature and the focal point of the mirror.

  • How is the location of the image determined graphically in the script?

    -The location of the image is determined by drawing two rays: one parallel to the normal that reflects through the focal point, and the other from the top of the object through the focal point that reflects off the mirror.

  • What mathematical equation is used to find the image distance (S') in the script?

    -The equation used to find the image distance is S' = (SF / (s - f)), where S is the object distance, F is the focal length, and f is the distance from the lens to the focal point.

  • What was the object distance (s) given in the script?

    -The object distance (s) given in the script is 40 cm.

  • How is the image distance calculated in the script?

    -The image distance is calculated as 1000 / 15, which equals approximately 66.7 cm.

  • What does the positive value of the image distance indicate about the image?

    -A positive value of the image distance indicates that the image is real, meaning it is formed on the same side of the mirror as the light source.

  • What is the magnification of the image found in the script?

    -The magnification of the image is found to be 1.67 times the size of the original object.

  • What does the negative sign in the magnification indicate?

    -The negative sign in the magnification indicates that the image is inverted, or upside down.

Outlines
00:00
🔍 Exploring Concave Mirrors: Second Example

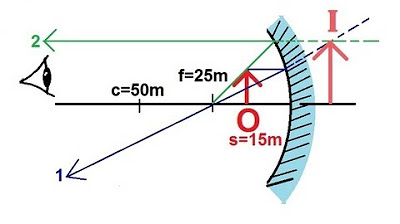
In this section, we continue our exploration of concave mirrors, which have positive focal lengths. We consider a mirror with a focal length of 25 cm, making the distance to the center of curvature 50 cm. The object is placed between the center of curvature and the focal point, unlike the previous example where it was placed farther away. We begin by graphically determining the image location by drawing rays and finding their intersection point. This method shows the image appears to be beyond the center of curvature. For a precise location, we use the mirror equation, calculating the image distance (S') to be approximately 66.7 cm. The image is real, as indicated by the positive value and its position in front of the mirror. We also calculate the magnification, which is -1.67, indicating the image is inverted and 1.67 times larger than the object. Thus, we conclude the image is real, inverted, and magnified.

Mindmap
Keywords
💡Concave Mirror
A concave mirror is a type of mirror with a curved surface that bulges inward. It has the ability to converge light rays to a single point known as the focal point. In the video, the concave mirror with a 25 cm focal length is used to demonstrate the principles of image formation and the effect of object placement on the image's characteristics.
💡Focal Length
The focal length of a mirror or lens is the distance from the optical center to the point where parallel light rays converge or appear to diverge. In the context of the video, the concave mirror has a positive focal length of 25 cm, indicating that the mirror is capable of focusing light to a point 25 cm away from the mirror's surface.
💡Center of Curvature
The center of curvature is the midpoint of the sphere from which a spherical mirror is cut. It is twice the distance from the mirror's surface to the focal point. In the video, the center of curvature is 50 cm away from the lens, which is important for understanding the geometry of the mirror and its effect on image formation.
💡Object Distance
Object distance refers to the distance between the object and the optical system, such as a lens or mirror. In the video, the object is placed 40 cm away from the concave mirror, which is a critical parameter in determining the location and characteristics of the image formed by the mirror.
💡Image Distance
Image distance is the distance from the optical system to the image formed by it. The video script uses the mirror equation to calculate the image distance (S') as 66.7 cm, which helps in understanding the position of the image relative to the mirror.
💡Mirror Equation
The mirror equation, 1/f = 1/do + 1/di, is used to calculate the relationship between the focal length (f), the object distance (do), and the image distance (di). In the video, this equation is applied to find the exact location of the image formed by the concave mirror.
💡Ray Tracing
Ray tracing is a method used to predict the path of light rays as they interact with optical systems. The video script describes the graphical method of tracing two key rays to determine the approximate location of the image formed by the concave mirror.
💡Real Image
A real image is formed when the light rays converge to form an image on a screen. In the video, the image is determined to be real because it is located beyond the focal point and in front of the mirror, as indicated by the positive value of the image distance.
💡Magnification
Magnification is the ratio of the image size to the object size and is a measure of how much an image is enlarged or reduced by an optical system. The video calculates the magnification to be 1.67, indicating that the image is larger than the object.
💡Inverted Image
An inverted image is one where the top and bottom of the object are reversed in the image. The video script mentions that the magnification is negative, which indicates that the image is not only larger but also inverted relative to the object.
Highlights

The example demonstrates finding the image of an object placed in front of a concave mirror using both graphical and mathematical methods.

Concave mirrors have positive focal lengths, and the example uses a mirror with a 25 cm focal length.

The distance from the lens to the center of curvature is twice the focal length, which is 50 cm in this example.

The object is placed between the center of curvature and the focal point of the mirror.

Graphical method is used first to approximate the location of the image by drawing rays.

The first ray is drawn parallel to the normal and reflects through the focal point.

The second ray is drawn from the top of the object through the focal point and reflects off the mirror.

The location where the two rays meet approximates the position of the image.

Mathematics is then used to find the exact location of the image using the equation S' = SF / (s - f).

The object distance (s) is given as 40 cm from the mirror.

The image distance (S') is calculated to be approximately 66.7 cm from the mirror.

The image is real since it is in front of the mirror and has a positive image distance.

Magnification is calculated using the equation M = -S' / s, resulting in 1.67 times magnification.

The negative sign in the magnification indicates that the image is inverted.

The process demonstrates how to find the image of an object placed between the center curvature and focal point of a concave mirror.

The next example will move the object closer to the mirror, between the focal point, to see where the image appears.

Transcripts

Browse More Related Video

Physics - Optics: Lenses (3 of 4) Converging Lens

Physics 54 Optics: Mirrors (3 of 6) Concave Mirror

Physics - Optics: Lenses (1 of 4) Converging Lens

Physics - Optics: Lenses (2 of 4) Converging Lens

Physics - Optics: Lenses (4 of 5) Lens Combinations - Converging & Diverging Lenses

Physics 54 Optics: Mirrors (4 of 6) Convex Mirror

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Concave MirrorOpticsImage FormationFocal LengthRay TracingMirror EquationReal ImageMagnificationInverted ImagePhysics Tutorial