Physics 51 - Optics: Reflections (2 of 2) Inbound and Exit Ray

Michel van Biezen
28 Apr 201303:54
EducationalLearning
32 Likes 10 Comments

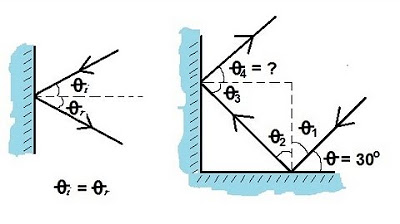
TLDRThis lecture demonstrates the process of calculating the angle change of a light ray reflecting off two surfaces that are not at a right angle. It begins by illustrating the law of reflection for the first surface, establishing equal angles of incidence and reflection. The second reflection involves drawing a horizontal reference line to determine the angles of incidence and reflection for the second surface, which are found to be 50 degrees each. The total angle change is calculated by summing the individual angles, revealing that the exiting ray is 20 degrees away from being parallel to the inbound ray, providing a clear method to understand reflection in non-right angle scenarios.

Takeaways
  • 🔍 The lecture discusses a method for calculating the angle between an inbound and an exiting ray after two reflections, which is not a simple corner reflector scenario.
  • 📐 The first step is to identify the normal to the surface and the angle of incidence (theta sub one), which equals the angle of reflection (theta sub two) due to the law of reflection.
  • 🔄 The inbound ray is reflected off the first surface, and the angle of incidence is equal to the angle of reflection, forming a 30-degree angle in this example.
  • 📏 After the first reflection, the ray hits the second surface, and the angle of incidence (theta sub three) is calculated by considering the geometry of the situation.
  • 📐 The angle of reflection off the second surface (theta sub four) is determined to be equal to theta sub three, which is 50 degrees, following the law of reflection.
  • 📊 The total angle change for the ray after two reflections is calculated by adding the angles of incidence and reflection from both surfaces, summing up to 160 degrees.
  • 📈 The final angle between the inbound and exiting ray is found by considering the parallel lines formed by extending the rays, which results in a 20-degree angle.
  • 📝 The process involves drawing horizontal and perpendicular lines to establish reference points and angles, which are crucial for calculating the angles of incidence and reflection.
  • 📈 The script uses the sum of interior angles of a triangle to deduce the unknown angles, applying geometric principles to the problem.
  • 📚 The lecture demonstrates the importance of understanding geometric relationships and the law of reflection in optical problems.
  • 🔎 The method can be applied to more complex optical systems where rays undergo multiple reflections, providing a systematic approach to solving such problems.
Q & A

  • What is the main topic of the lecture?

    -The main topic of the lecture is the method of dealing with reflection in optics, specifically how to calculate the angle between an inbound ray and an exiting ray when reflecting off surfaces that are not at a 90-degree angle.

  • What is the significance of the normal in the first reflection?

    -The normal is significant in the first reflection because it helps determine the angle of incidence (theta sub one), which is equal to the angle of reflection (theta sub two), according to the law of reflection.

  • Why is it necessary to draw a normal to the surface for the second reflection?

    -Drawing a normal to the surface for the second reflection is necessary to determine the new angle of incidence (theta sub three) and the angle of reflection (theta sub four), which are crucial for calculating the final exiting angle of the ray.

  • What is the relationship between theta sub one and theta sub two?

    -Theta sub one and theta sub two are related by the law of reflection, which states that the angle of incidence is equal to the angle of reflection, hence theta sub one equals theta sub two.

  • How is the angle of reflection for the second surface determined?

    -The angle of reflection for the second surface is determined by using the horizontal line as a reference and recognizing that the sum of angles in a triangle must equal 180 degrees, leading to the conclusion that theta sub three and theta sub four are both 50 degrees.

  • What is the total sum of the angles involved in the reflection process?

    -The total sum of the angles involved in the reflection process is 160 degrees, which includes theta sub one (30 degrees), theta sub two (30 degrees), theta sub three (50 degrees), and theta sub four (50 degrees).

  • Why are the two lines that extend from the points of reflection parallel to each other?

    -The two lines are parallel because the sum of the angles on one side of the ray equals 180 degrees, indicating that the lines are extended in the same direction, making them parallel.

  • What is the angle between the inbound and exiting ray after all reflections?

    -The angle between the inbound and exiting ray after all reflections is 20 degrees, which is calculated by subtracting the total sum of the angles (160 degrees) from 180 degrees.

  • How does the讲师 use the concept of a triangle to find theta sub three?

    -The lecturer uses the concept of a triangle by recognizing that the sum of angles in a triangle is 180 degrees. By knowing one angle is 60 degrees and another is 30 degrees, the讲师 deduces that the remaining angle must be 90 degrees minus 30 degrees, which is 60 degrees, and then further calculates theta sub three to be 50 degrees.

  • What is the significance of the 20-degree angle mentioned at the end of the script?

    -The 20-degree angle mentioned at the end of the script is the angle between the two lines that would be parallel if extended, indicating the final angle between the inbound and exiting rays after all reflections.

Outlines
00:00
🔍 Understanding Non-Right Angle Reflections

This paragraph discusses a complex reflection scenario involving an inbound ray and a surface that is not at a right angle. The lecturer introduces the concept of normal lines and the angles of incidence and reflection, emphasizing the equality of these angles. The explanation involves calculating the angles at each reflection point, using geometric principles to deduce the final angle between the inbound and exiting rays. The process includes identifying a 30-degree angle at the first reflection, drawing a horizontal reference line, and using it to determine subsequent angles, concluding with the calculation of the total angle change and the final angle between the two rays, which is 20 degrees.

Mindmap
Keywords
💡Reflection
Reflection refers to the change in direction of a wavefront at an interface between two different media so that the wavefront returns to the medium from which it originated. In the context of the video, reflection is used to describe the behavior of light rays bouncing off surfaces, which is central to understanding how light interacts with objects.
💡Normal
A normal is a line perpendicular to a surface at a given point. It is a fundamental concept in geometry and optics, especially when discussing reflections. In the script, the normal is used to determine the angles of incidence and reflection, which are crucial for calculating the path of light rays after they bounce off a surface.
💡Angle of Incidence
The angle of incidence is the angle at which a ray or wave approaches a surface. It is measured from the normal to the surface. In the video, the angle of incidence is used to describe the initial angle at which the light ray hits the first surface, and it is equal to the angle of reflection according to the law of reflection.
💡Angle of Reflection
The angle of reflection is the angle at which a ray or wave leaves a surface after reflecting off it. It is equal to the angle of incidence, as stated by the law of reflection. In the video, the concept is used to explain how the light ray changes direction after bouncing off the first surface.
💡Inbound Ray
An inbound ray is a light ray that is entering a new medium or surface. In the script, the inbound ray is the initial light ray that strikes the first surface, and its angle is measured to determine the subsequent reflection angles.
💡Exiting Ray
The exiting ray is the light ray that leaves a surface after reflection. The video aims to find the angle between the inbound ray and the exiting ray, which helps in understanding the total change in direction of the light as it interacts with the surfaces.
💡Theta Subscripts
Theta with subscripts (e.g., theta sub one, theta sub two, etc.) is used in the script to denote different angles involved in the reflection process. Each subscript represents a specific angle at a particular stage of the reflection, helping to track and calculate the overall change in the light ray's direction.
💡Law of Reflection
The law of reflection states that the angle of incidence is equal to the angle of reflection. This principle is fundamental in understanding how light behaves when it interacts with surfaces. The video script applies this law to explain the relationship between the angles of incidence and reflection for each surface the light ray encounters.
💡Perpendicular
Perpendicular lines are lines that intersect at a right angle, which is 90 degrees. In the context of the video, perpendicular lines are used to define the normal to the surfaces and to establish reference angles for calculating the angles of incidence and reflection.
💡Parallel Lines
Parallel lines are lines in a plane that do not meet; they are always the same distance apart. In the script, the concept of parallel lines is used to determine the final angle between the inbound and exiting rays, by showing that the sum of the angles around a point is 180 degrees, indicating that the lines would be parallel if extended.
💡Geometry
Geometry is the branch of mathematics concerned with the properties and relations of points, lines, surfaces, and solids in space. The video script heavily relies on geometric principles, such as angles, perpendicular lines, and triangles, to explain the behavior of light rays as they reflect off surfaces.
Highlights

Introduction to dealing with reflection in a more complex scenario that is not a corner reflector.

Explanation of the first reflection and the importance of the normal to the surface.

Identification of theta sub one as the angle of incidence equaling the angle of reflection.

Calculation of theta sub two as the angle of reflection, given a 60-degree angle.

Introduction of the second reflection and drawing a normal to the surface.

Determination of theta sub three and theta sub four as the angles of incidence and reflection for the second reflection.

Use of a horizontal reference line to help determine the angles involved in the second reflection.

Calculation of the 60-degree angle in the triangle formed by the reflected ray and the normal.

Determination that theta sub three is 50 degrees based on the angles included by the lines.

Confirmation that theta sub four is also 50 degrees due to the law of reflection.

Explanation of how the total angle change is calculated by adding the angles of reflection.

Conclusion that the total angle sum is 160 degrees, indicating the rays are not parallel.

Final calculation showing the angle between the inbound and exit ray is 20 degrees.

Demonstration of the method to calculate the angle change in a non-right angle reflection scenario.

Transcripts

Browse More Related Video

Law of Reflection - Geometric Optics - Physics

Laws of Reflection | #aumsum #kids #science #education #children

Physics 51 - Optics: Reflections (1 of 2) Introduction

GCSE Physics - Reflection #62

Specular Reflection

Physics 52 Refraction and Snell's Law (5 of 11) The Fiber Optic Cable

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Light ReflectionGeometry TutorialOptics BasicsAngle CalculationPhysics LessonEducational ContentRay TracingSurface InteractionAcademic LectureOptical Phenomena