Power Series Practice | MIT 18.01SC Single Variable Calculus, Fall 2010

MIT OpenCourseWare
7 Jan 201110:03
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the instructor guides viewers through the process of identifying functions represented by four given power series. The focus is on manipulating series to resemble known functions, assuming convergence. The examples include transforming a series into \( e^x \) by factoring, adjusting a geometric series to match its standard form, and splitting a series into known components. The video concludes by demonstrating sigma notation manipulation to simplify a series into a recognizable geometric progression.

Takeaways
  • 📚 The video is a tutorial focused on manipulating power series to identify the functions they represent.
  • 🔍 The instructor assumes that the x-values used will ensure the convergence of the series, so students need not worry about convergence issues.
  • 📝 The goal for each problem (a), (b), (c), and (d) is to express the series as a specific function without a summation sign.
  • 🤔 The process involves manipulating the series to resemble known functions, such as exponential or geometric series.
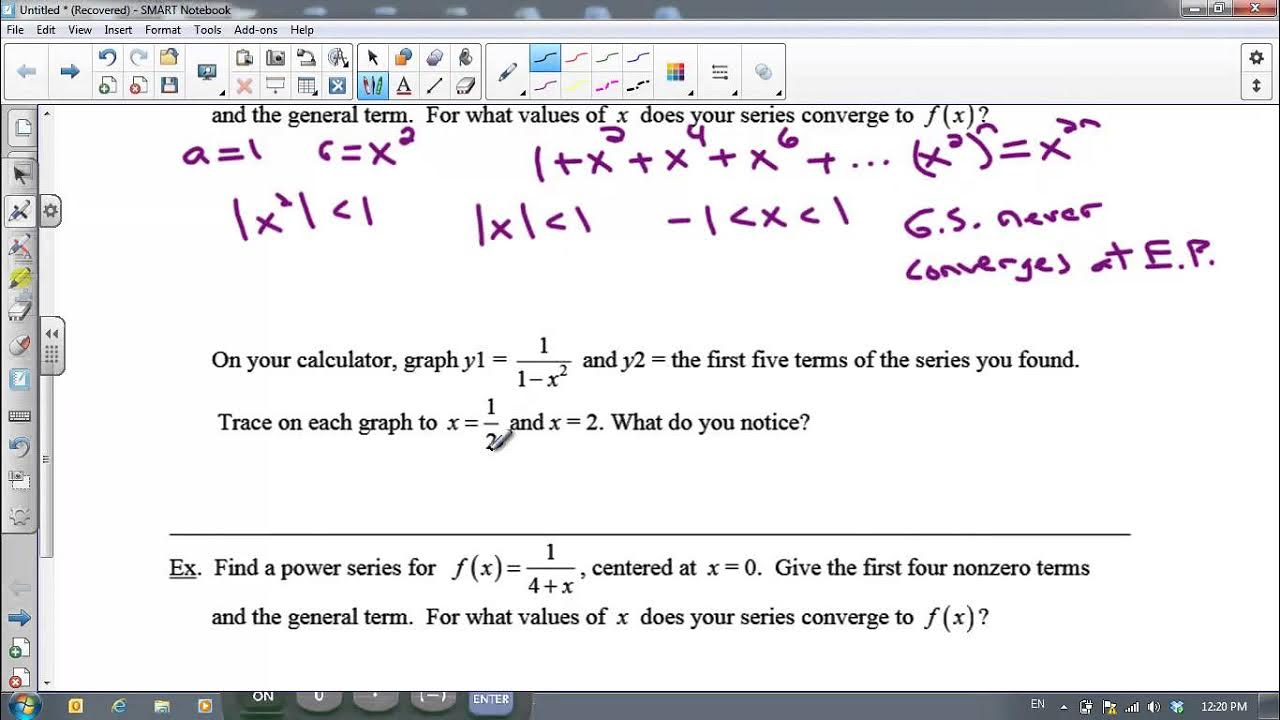
  • 📈 For problem (a), the series is manipulated to resemble e^x by factoring out x^2 and recognizing the remaining sum as e^x.
  • 🔗 In problem (b), the series is rewritten as a geometric series and then adjusted by subtracting the extra terms added to align with the known series.
  • 📉 Problem (c) involves splitting the series into two separate known series and identifying each part individually.
  • 🔄 For problem (d), the instructor demonstrates the manipulation of sigma notation by changing the index of summation to simplify the expression.
  • 📐 The video emphasizes the importance of recognizing and manipulating series to match known functions, showcasing different techniques for doing so.
  • 🧩 The exercises in the video are designed to test and reinforce understanding of series manipulation and convergence.
  • 🎓 The final takeaway is the ability to transform and simplify series expressions into recognizable functions, a key skill in mathematical analysis.
Q & A

  • What is the primary goal of the recitation video?

    -The primary goal is to manipulate given power series to find the corresponding functions they represent.

  • What assumption is made about the x-values in the given power series?

    -It is assumed that the x-values used in the power series are ones that ensure the sums converge.

  • How is the series in part (a) of the problems rewritten to identify the function it represents?

    -The series in part (a) is rewritten by factoring out x^2, allowing the remaining series to be recognized as the series for e^x, resulting in x^2 * e^x.

  • Why does the solution for part (b) involve adjusting the starting index of the summation?

    -The solution for part (b) involves adjusting the starting index to convert it into a geometric series and then subtracting the extra terms added in the process.

  • How is the function for the series in part (b) determined?

    -The function is determined by recognizing the series as a geometric series starting from n=0 and then subtracting the x^0 and x^1 terms to maintain equality, resulting in 1/(1-x) - 1 - x.

  • What is the significance of treating the series like polynomials in part (c)?

    -Treating the series like polynomials allows the series to be split into known functions, specifically e^x and 1/(1-x), simplifying the overall expression.

  • How is the summation index adjusted in part (d) to make the series more recognizable?

    -The summation index in part (d) is adjusted by shifting it to start from m=0 instead of n=-1, making it easier to identify the series as a geometric series.

  • What is the resulting function for the series in part (d) after adjusting the index?

    -After adjusting the index, the resulting function for the series is identified as 1/(1-x).

  • What is the overall purpose of manipulating the series in these problems?

    -The overall purpose is to transform the series into known functions, leveraging familiarity with common series like e^x and the geometric series.

  • How does the recitation video help students understand power series better?

    -The recitation video helps students understand power series better by demonstrating how to manipulate and recognize them as known functions, reinforcing concepts from the lecture.

Outlines
00:00
📚 Power Series Manipulation and Function Identification

This paragraph introduces a video tutorial focused on manipulating power series to identify the functions they represent. The instructor presents four problems and encourages viewers to pause the video to work through them. The goal is to transform the series into a form that no longer includes a sum, but rather a specific function. The instructor emphasizes that the x-values are chosen to ensure convergence, so viewers need not worry about convergence issues. The paragraph concludes with the instructor's return to demonstrate the solution process for the problems.

05:02
🔍 Analyzing and Transforming Power Series

The second paragraph delves into the process of analyzing and transforming power series. The instructor demonstrates how to manipulate series to resemble known functions, using the properties of polynomials and series. The paragraph covers four examples: (a) shows how to factor out common terms and relate the series to the exponential function e^x; (b) discusses the manipulation of a geometric series missing initial terms; (c) illustrates the addition of two separate series to form a known function; and (d) examines the sigma notation for a series starting with a negative index. The instructor uses these examples to teach viewers how to recognize and manipulate series into familiar forms, emphasizing the importance of understanding the underlying mathematical concepts.

Mindmap
Keywords
💡Power Series
A power series is an infinite sum of terms in the form of a_n * x^n, where a_n represents the coefficients and x is the variable. In the video, power series are manipulated to represent specific functions, demonstrating how they can be rewritten and simplified.
💡Convergence
Convergence refers to the behavior of a series as its terms approach a limit. A series converges if the sum of its terms approaches a finite value. The video assumes that the power series provided are convergent, meaning the sums have finite values for certain x-values.
💡Function Representation
Function representation involves expressing a function as a power series. The video focuses on identifying the functions represented by given series, such as rewriting a series to show it equals a known function like e^x.
💡e^x (Exponential Function)
e^x is the exponential function, which can be expressed as the power series sum of x^n/n!. The video uses this function to illustrate how certain power series can be identified and rewritten to match known functions.
💡Geometric Series
A geometric series is a series where each term is a constant multiple of the previous term. The sum of a geometric series from n=0 to infinity is 1/(1-x) for |x|<1. The video manipulates power series to fit this form and identify the functions they represent.
💡Sigma Notation
Sigma notation is a way to write sums concisely using the Greek letter sigma (Σ) to represent the sum. The video uses sigma notation to express the power series and demonstrates how to manipulate and simplify these expressions.
💡Factorial
Factorial, denoted n!, is the product of all positive integers up to n. It appears in the power series for e^x as x^n/n!. The video uses factorials in series manipulations to identify functions like the exponential function.
💡Polynomial
A polynomial is a mathematical expression involving a sum of powers in one or more variables multiplied by coefficients. The video treats power series like polynomials, factoring and combining terms to simplify and identify the represented functions.
💡Manipulation
Manipulation in this context refers to algebraically altering the form of a series to make it resemble known functions. The video demonstrates various techniques to rewrite and combine series, making it easier to identify the underlying functions.
💡Summation Index
The summation index is the variable (often n or k) used in sigma notation to denote the terms of the series being summed. The video changes summation indices to simplify series and match them to known functions, such as adjusting indices to start at different values.
Highlights

Introduction to the task of identifying functions represented by power series.

Assumption that x-values ensure convergence of the series sums.

Goal to transform the series into a specific function without a sum.

Guidance to pause the video for practice before revealing solutions.

Enthusiasm for series manipulation and its educational value.

Explanation of rewriting series to resemble known functions.

Identification of series (a) resembling the exponential function e^x.

Factoring out x^2 from series (a) to simplify it to x^2 * e^x.

Series (b)'s resemblance to a geometric series with missing terms.

Adjusting series (b) by adding and subtracting terms to match a known series.

Revealing the sum of series (b) as 1/(1-x) after adjustments.

Approach to splitting series (c) into two known convergent series.

Identification of series (c) components as e^x and 1/(1-x).

Understanding sigma notation and manipulating indices in series (d).

Transformation of series (d) into a recognizable geometric series form.

Final revelation of series (d) as the geometric series sum.

Summary of the exercise's purpose: manipulating series to match known functions.

Transcripts

Browse More Related Video

Geometric series interval of convergence | Series | AP Calculus BC | Khan Academy

AP Calculus BC Lesson 10.14 Part 2

Geometric Series Summing to Functions

Alternating Series

Taylor Series Day 3

Calculus 2 Lecture 9.2: Series, Geometric Series, Harmonic Series, and Divergence Test

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Power SeriesMathematicsEducationalSeries ManipulationConvergenceGeometric SeriesE to the xFactorial SeriesSummation NotationSeries AnalysisMath Recitation