Hyperbolic Trig Sub | MIT 18.01SC Single Variable Calculus, Fall 2010

MIT OpenCourseWare

7 Jan 201116:27

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, the instructor introduces a hyperbolic trigonometric substitution technique for solving integrals. The lesson focuses on calculating the area under a hyperbola using the hyperbola equation \( x^2 - y^2 = 1 \) and a point \( (cosh(t), sinh(t)) \). The instructor guides the audience through setting up the integral and suggests a substitution based on the hyperbolic identity \( sinh^2(u) + 1 = cosh^2(u) \) to simplify the problem. The video concludes with the integral's solution and a comparison to the regular trigonometric functions, highlighting the utility of hyperbolic trig substitutions in certain integral forms.

Takeaways

📚 The lesson introduces a variation on trigonometric substitution known as hyperbolic trigonometric substitution, used to simplify integrals of certain forms.
📐 The example provided involves a hyperbola defined by the equation \( x^2 - y^2 = 1 \) and a point on the hyperbola at coordinates \( (\cosh(t), \sinh(t)) \).
🔍 The formulas for hyperbolic cosine \( \cosh(t) \) and hyperbolic sine \( \sinh(t) \) are given as \( \cosh(t) = \frac{e^t + e^{-t}}{2} \) and \( \sinh(t) = \frac{e^t - e^{-t}}{2} \).
📈 The region of interest for finding the area is bounded by the hyperbola, the x-axis, and a line segment from the origin to the point \( (\cosh(t), \sinh(t)) \).
🔺 The integral to find the area is set up by considering horizontal rectangles and integrating with respect to \( y \) from 0 to \( \sinh(t) \).
✂️ The integral is split into two parts: one involving the square root of \( y^2 + 1 \) and another involving \( y \) multiplied by a constant.
🔄 A hyperbolic trig substitution \( y = \sinh(u) \) is suggested to simplify the square root part of the integral, leveraging the identity \( \sinh^2(u) + 1 = \cosh^2(u) \).
📉 The substitution simplifies the integral to \( \int \cosh^2(u) \, du \), which can be further simplified using the exponential form of the hyperbolic cosine function.
📝 The integral is computed in two steps: first, integrating the polynomial part directly, and second, applying the hyperbolic trig substitution to the square root part.
🧩 The final area of the region is found to be \( \frac{t}{2} \), which is a neat result highlighting the relationship between the hyperbolic function and the area under consideration.
🔑 The lesson concludes with the insight that hyperbolic trig substitutions can be a powerful tool in integral calculus, especially for integrals that exhibit certain forms.

Q & A

What is the main topic discussed in the video script?
-The main topic discussed in the video script is the hyperbolic trigonometric substitution, a technique used in calculus to solve integrals involving hyperbolic functions.
What is the hyperbolic trigonometric substitution?
-The hyperbolic trigonometric substitution is a method used to simplify the integration of functions that resemble the form of a hyperbolic identity, such as \( \sqrt{y^2 + 1} \), by substituting with a hyperbolic function, in this case, \( y = \sinh(u) \).
What is the region whose area is being calculated in the script?
-The region whose area is being calculated is the area below the line segment connecting the origin to the point \( (\cosh(t), \sinh(t)) \) on the hyperbola \( x^2 - y^2 = 1 \), above the x-axis, and to the left of the hyperbola's right branch.
What are the coordinates of the chosen point on the hyperbola?
-The chosen point on the hyperbola has coordinates \( (\cosh(t), \sinh(t)) \), where \( \cosh(t) \) is the hyperbolic cosine and \( \sinh(t) \) is the hyperbolic sine of \( t \).
What is the integral set up to find the area of the region?
-The integral set up to find the area of the region is an integral with respect to \( y \), from \( y = 0 \) to \( y = \sinh(t) \), of the difference between the rightmost x-coordinate, \( \sqrt{y^2 + 1} \), and the leftmost x-coordinate, \( \frac{\cosh(t)}{\sinh(t)}y \).
What is the significance of the hyperbolic identity used in the substitution?
-The hyperbolic identity \( \sinh^2(u) + 1 = \cosh^2(u) \) is used to simplify the integrand \( \sqrt{y^2 + 1} \) after the substitution \( y = \sinh(u) \), allowing the integral to be expressed in terms of \( \cosh(u) \), which is easier to integrate.
How does the script suggest simplifying the integral involving \( y \)?
-The script suggests simplifying the integral involving \( y \) by recognizing it as a constant times \( y \) and then integrating from 0 to \( \sinh(t) \), resulting in \( -\frac{\cosh(t)\sinh(t)}{2} \).
What is the final result of the area calculation?
-The final result of the area calculation is \( \frac{t}{2} \), which is obtained by adding the results of the two integrals after applying the hyperbolic trigonometric substitution.
What is the analogy mentioned at the end of the script between hyperbolic trig functions and regular trig functions?
-The analogy mentioned is that just as the area of a triangle formed by a point on a unit circle at \( (\cos(\theta), \sin(\theta)) \) is \( \frac{\theta}{2} \), the area of the region under consideration in the script is \( \frac{t}{2} \), where \( t \) plays a similar role to \( \theta \) in measuring the area.
What is the practical application of the hyperbolic trig substitution discussed in the script?
-The practical application of the hyperbolic trig substitution discussed in the script is to solve integrals of certain forms more efficiently, particularly when the integrand resembles a hyperbolic identity, offering an alternative to traditional trigonometric substitutions.

Outlines

00:00

📚 Introduction to Hyperbolic Trigonometric Substitution

The video begins with an introduction to a special type of trigonometric substitution, specifically the hyperbolic trigonometric substitution, which is used to simplify the computation of areas under certain curves. The presenter illustrates the concept by discussing a problem involving the area under a hyperbola defined by the equation x^2 - y^2 = 1. A point on this hyperbola is given as (cosh t, sinh t), where cosh and sinh are the hyperbolic cosine and sine functions, respectively. The presenter sets up the integral to find the area of the region bounded by the hyperbola, the x-axis, and a line segment from the origin to the point (cosh t, sinh t), and suggests using horizontal rectangles for the integration due to its simplicity.

05:00

🔍 Setting Up the Integral for Area Calculation

The presenter continues by detailing the process of setting up the integral to calculate the area of the specified region. The integral is set up with respect to y, integrating from y = 0 to y = sinh t. The right and left bounds for the x-coordinates of the rectangles are determined by the hyperbola's equation and the line passing through the origin, respectively. The integral to be evaluated involves the square root of y squared plus 1, which is simplified by recognizing it as the hyperbolic cosine function. The presenter also addresses the integral of a constant times y, which is straightforward to solve.

10:02

🧑‍🏫 Applying Hyperbolic Trigonometric Substitution

The presenter suggests a hyperbolic trig substitution, y = sinh u, to simplify the integral involving the square root of y squared plus 1. This substitution is based on the hyperbolic identity sinh squared u plus 1 equals cosh squared u. The presenter guides the viewer to make this substitution, change the differential from dy to du, and adjust the integration bounds accordingly. The integral then becomes a simpler form involving cosh squared u, which can be integrated using the exponential function representation of the hyperbolic cosine.

15:03

📈 Conclusion and Analogy with Regular Trigonometric Functions

The presenter concludes by solving the integral and finding the area of the region to be t over 2, where t is the parameter in the hyperbolic functions. The result is highlighted as a neat analogy to the area calculation in regular trigonometric functions, where the area under the curve from 0 to theta is theta over 2. The presenter emphasizes the usefulness of hyperbolic trig substitutions in integrals that suggest their form and encourages viewers to consider them as part of their mathematical toolkit.

Mindmap

Keywords

💡Hyperbolic Trigonometric Substitution

Hyperbolic trigonometric substitution is a mathematical technique used to simplify integrals that involve expressions like the square root of a sum of squares, which are common in hyperbolic geometry. In the video, this technique is introduced as a method to compute the area of a region bounded by a hyperbola and a line segment. The substitution y = sinh(u) is used to transform the integral into a more manageable form using the identity sinh^2(u) + 1 = cosh^2(u).

💡Hyperbola

A hyperbola is a type of conic section defined by the set of all points where the difference of the distances to two fixed points (foci) is constant. In the context of the video, the hyperbola x^2 - y^2 = 1 is used to define a region in the coordinate plane, and the problem involves finding the area of a specific region bounded by part of this hyperbola, a line segment, and the x-axis.

💡Cosh and Sinh

Cosh (hyperbolic cosine) and sinh (hyperbolic sine) are functions that are part of the hyperbolic functions, which are analogous to the regular trigonometric functions but involve exponentials. In the video, cosh(t) and sinh(t) are used to describe a point on the hyperbola, with cosh(t) defined as (e^t + e^(-t))/2 and sinh(t) as (e^t - e^(-t))/2.

💡Integral

An integral is a fundamental concept in calculus representing the area under a curve or the accumulation of a quantity. In the video, the integral is used to calculate the area of a specific region in the coordinate plane, which is approached by setting up an integral with respect to y and then simplifying it using a substitution.

💡Area Computation

Area computation is the process of determining the size of a two-dimensional region. In the video, the focus is on computing the area of a region bounded by a hyperbola and a line segment using integral calculus, which involves setting up and solving an integral to find the total area.

💡Vertical and Horizontal Rectangles

In the context of integration, vertical and horizontal rectangles refer to the method of approximating the area under a curve by dividing the region into rectangles aligned with the coordinate axes. The video discusses the choice between using vertical or horizontal rectangles to simplify the computation of the area of the given region, ultimately choosing horizontal rectangles for ease of integration.

💡Trigonometric Identity

A trigonometric identity is an equation that holds true for all values of the variables where both sides of the equation are defined. In the video, the identity tan^2(x) + 1 = sec^2(x) is mentioned, and an analogous hyperbolic trig identity, sinh^2(u) + 1 = cosh^2(u), is used to facilitate the substitution in the integral.

💡Substitution

Substitution is a technique used in calculus to simplify integrals by replacing a variable with another expression. In the video, the hyperbolic trig substitution y = sinh(u) is used to transform the integral into a form that can be more easily evaluated.

💡Exponential Functions

Exponential functions are mathematical functions of the form f(x) = a^x, where 'a' is a positive real number not equal to 1. In the video, the formulas for cosh and sinh involve exponential functions, and the integral involving cosh^2(u) is simplified by expressing it in terms of exponential functions.

💡Hyperbolic Cotangent

Hyperbolic cotangent, written as coth(x), is one of the hyperbolic functions. It is the inverse of the hyperbolic tangent function. In the video, while not central to the computation, coth(t) is mentioned as an alternative way to express cosh(t)/sinh(t), providing a connection to the broader family of hyperbolic functions.

💡Analytical Geometry

Analytical geometry, also known as coordinate geometry, is a branch of mathematics that deals with the study of geometric objects by using a coordinate system. The video uses analytical geometry to define the hyperbola and the region of interest in the coordinate plane and to set up the integral for area computation.

Highlights

Introduction to hyperbolic trigonometric substitution as a variation of trig substitution.

The problem involves computing the area of a region bounded by a hyperbola and a line segment.

The hyperbola equation is x^2 - y^2 = 1, with a point (cosh t, sinh t) on it.

Definitions of hyperbolic cosine (cosh t) and sine (sinh t) using exponential functions.

Explanation of how the point (cosh t, sinh t) lies on the right branch of the hyperbola.

The choice between vertical and horizontal rectangles for integration, with a preference for the latter.

Setting up the integral for the area using horizontal rectangles and the bounds on y.

Solving for x in terms of y to find the rightmost x-coordinate of the rectangles.

The leftmost x-coordinate is derived from the line equation y = sinh t / cosh t * x.

The integral to find the area involves a square root of y squared plus 1.

Suggestion of a hyperbolic trig substitution y = sinh u to simplify the integral.

The use of the hyperbolic identity sinh^2 u + 1 = cosh^2 u in the substitution.

Integration of the polynomial part of the integral involving y.

Application of the hyperbolic trig substitution to the square root part of the integral.

Transformation of the integral using the substitution and hyperbolic identity.

Integration of the resulting expression involving cosh^2 u.

Simplification of the integral using exponential functions for cosh.

Final computation of the integral and the area of the region.

Observation of the analogy between the area measured by theta in circle trigonometric functions and t in hyperbolic functions.

Conclusion on the utility of hyperbolic trig substitution in certain integral forms.

Transcripts

Browse More Related Video

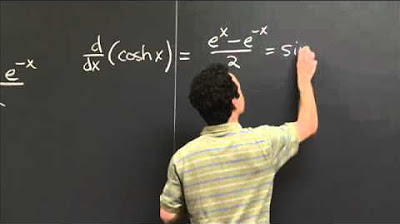
Hyperbolic trig functions | MIT 18.01SC Single Variable Calculus, Fall 2010

GENERAL EQUATION OF THE HYPERBOLA IN STANDARD FORM || PRE-CALCULUS

U-Substitution with Definite Integrals

Line integral example 1 | Line integrals and Green's theorem | Multivariable Calculus | Khan Academy

Lec 28 | MIT 18.01 Single Variable Calculus, Fall 2007

Lesson 4 - Inverse Hyperbolic Functions (Calculus 2 Tutor)