Tensor Calculus Lecture 11a: Gauss' Theorema Egregium, Part 1
TLDRIn this lecture, the speaker enthusiastically delves into the intricacies of Gauss's Theorema Egregium, a highlight of the series. Despite a sore throat, the lecturer's passion for the topic is palpable. The session begins with a redemption calculation from the previous lecture and progresses through warm-up exercises. The main focus is on deriving the relationship between surface and ambient Christoffel symbols, leading to the Gauss-Codazzi equations. The speaker emphasizes the elegance and significance of these mathematical explorations, which extend beyond pure geometry into realms like topology and relativity.
Takeaways
- 📚 The lecturer is excited to discuss 'Gus's theorem', indicating its significance and anticipation for the topic.
- 🗓 Despite being late and having a sore throat, the lecturer's enthusiasm for the subject is undeterred, emphasizing the importance of the lecture.
- 🔍 The lecture aims to derive 'Gus's theorem', which is described as elegant and significant, with a focus on the derivation process itself.
- 📈 The lecturer intends to start with a redemption calculation from the previous lecture, aiming for accuracy and setting the stage for the main theorem.
- 📝 The lecture will involve several calculations, with the lecturer viewing them as 'exhilarating journeys' rather than mere technicalities.
- 📐 The lecture will relate surface and ambient objects, starting with the surface Laplacian and ambient Laplacian, and moving towards the Christoffel symbols.
- 🔗 The relationship between the surface and ambient Christoffel symbols is crucial, leading to the Gaus-Codazzi equations, which are central to the derivation.
- 🌐 The lecturer mentions the importance of considering non-Euclidean spaces, suggesting that calculations will be more revealing in a general setting.
- 📉 The lecture will cover the commutator of tensors with ambient indices, which is a key step in understanding the relationship between surface and ambient spaces.
- 🎯 The ultimate goal is to derive the Gaus-Codazzi equations, which relate the intrinsic geometry of the surface to the extrinsic geometry of the ambient space.
- 📚 The lecturer encourages students to engage with the material, suggesting that the derivations are not just technical but also intellectually rewarding.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the derivation of Gauss's Theorema Egregium, a fundamental theorem in differential geometry.
What is the significance of Gauss's Theorema Egregium in the field of mathematics?
-Gauss's Theorema Egregium is significant because it relates the intrinsic curvature of a surface to the extrinsic curvature in the embedding space, connecting concepts in differential geometry, topology, and embedded surfaces.
What is the lecturer's attitude towards the calculations involved in the lecture?
-The lecturer views the calculations as exhilarating and sees each calculation as a journey, indicating a deep appreciation for the beauty of mathematical derivations.
What is the lecturer's strategy for the derivation of Gauss's Theorema Egregium?
-The lecturer's strategy involves a series of warm-up calculations to build up to the main derivation, starting with relating the surface Laplacian to the ambient Laplacian and then moving on to relate the surface Christoffel symbols to the ambient ones.
What is the role of the mean curvature in the calculations discussed in the lecture?
-The mean curvature plays a vital role in the calculations, as it appears in the expression relating the surface Laplacian to the ambient Laplacian, indicating its importance in the geometry of the surface.
What is the significance of the curvature tensor mentioned in the lecture?
-The curvature tensor, or the Riemann curvature tensor, is significant as it captures the intrinsic curvature properties of the space and is essential in deriving the relationship between the surface and ambient spaces.
How does the lecturer plan to handle the assumption of the ambient space being non-Euclidean?
-The lecturer plans to consider the theorem and calculations in a more general setting, where the ambient space is not necessarily Euclidean, to reveal more about the structure and implications of the theorem.
What is the 'projection formula' mentioned in the script, and how is it used?
-The 'projection formula' is a mathematical expression that relates the components of the shift tensor to the projection of the ambient space onto the surface. It is used to simplify calculations and relate surface quantities to ambient quantities.
What is the lecturer's approach to the calculation involving the Christoffel symbols?
-The lecturer's approach involves using the product rule and the chain rule to express the surface Christoffel symbols in terms of the ambient Christoffel symbols and the shift tensor.
What is the 'commutator' in the context of the lecture?
-In the context of the lecture, the 'commutator' refers to the difference between the covariant derivatives of a tensor when the indices are switched, which is used to explore the properties of the space and the relationships between indices.
How does the lecturer address the limitations of time and space in the lecture?
-The lecturer acknowledges the limitations of time and space by taking shortcuts in the derivation process where appropriate, focusing on the main goal of reaching the derivation of Gauss's Theorema Egregium.
Outlines
📚 Introduction to Gus's Theorem
The speaker expresses enthusiasm for discussing Gus's theorem, a topic they find particularly exciting. Despite being eager to end the lecture due to a sore throat, they are determined to cover the theorem, which they believe will be a highlight of the series. The significance of the theorem is mentioned as extending beyond the lecture's scope, touching on areas like topology and relativity. The lecture aims to derive the theorem, starting with a correction of a previous calculation mistake and moving on to warm-up exercises before delving into the main derivation. The setting for the calculations will be a general one, considering surfaces embedded in a non-Euclidean space.
🔍 Deriving the Relationship Between Surface and Ambient Laplacians
The paragraph focuses on the mathematical derivation of the relationship between the surface Laplacian and the ambient Laplacian. The process involves applying the chain rule and considering the normal and covariant derivatives. The speaker discusses the importance of mean curvature in the derivation and how it emerges as a significant factor. The final expression obtained relates the surface Laplacian to the ambient Laplacian, with additional terms involving the normal derivative and second-order normal derivative of a function U on the surface.
📘 Relating Surface Christoffel Symbols to Ambient Ones
This section delves into the relationship between surface and ambient Christoffel symbols. The speaker uses the shift tensor to relate the basis elements of the surface to those of the ambient space. The derivation involves applying the product rule and considering the chain rule for differentiation. The final result shows how the surface Christoffel symbols are related to the ambient ones, with a projection term and an additional term that vanishes in Euclidean spaces but is significant in non-Euclidean contexts.
🔗 Discussing the Commutator for Ambient Indices
The speaker introduces the concept of the commutator for tensors with ambient indices, such as the normal or shift tensor. They discuss the implications of the ambient space not being Euclidean and how this affects the calculation of the Christoffel symbols. The paragraph sets the stage for a deeper exploration of the commutator in the context of non-Euclidean spaces and its role in the derivation of Gauss's theorem.
🌐 Exploring Non-Euclidean Ambient Spaces
The paragraph explores the implications of working in a non-Euclidean ambient space, where the metric tensor is arbitrarily imposed and does not necessarily satisfy the conditions that would make the Riemann Christoffel symbol vanish. The speaker invites the audience to consider spaces where the metric tensor does not arise from a dot product, leading to a different kind of space known as a Riemannian space. This discussion is crucial for understanding the broader context of the derivation of Gauss's theorem.
🔄 Deriving the Commutator for Ambient Tensors
The speaker presents a shortcut to derive the commutator for tensors defined in the entire ambient space, even though the derivation is not fully valid for objects defined only on the surface. The calculation involves using the chain rule and considering the product rule. The final result is a boxed expression that relates the commutator to the Riemann Christoffel tensor, providing a crucial step towards deriving Gauss's theorem.
🎯 Preparing to Derive Gauss's Theorems
The final paragraph prepares the audience for the main event: the derivation of Gauss's theorems. The speaker acknowledges that the previous derivation, while not entirely valid, leads to the correct final answer. They encourage the audience to consider the implications for covariant indices and combinations of surface and ambient indices, hinting at the complexity of the upcoming derivation. The speaker then pauses to erase the board, signaling a transition to the next phase of the lecture.
Mindmap
Keywords
💡Gus's Theorem
💡Curvature Tensor
💡Christoffel Symbols
💡Covariant Derivative
💡Mean Curvature
💡Shift Tensor
💡Commutator
💡Riemann Curvature Tensor
💡Euclidean Space
💡Gauss-Codazzi Equations
Highlights
Introduction to the anticipation of discussing Gus's theorem, a favorite topic of the lecturer.
Emphasis on the significance of the theorem, touching upon areas such as topology, embedded surfaces, and intrinsic geometry.
The lecturer's eagerness to correct a calculation mistake from the previous lecture, showcasing dedication to accuracy.
Introduction of the concept of the ambient space and its role in the calculations, moving beyond the assumption of a Euclidean space.
Relating the surface Laplacian to the ambient Laplacian, highlighting the role of mean curvature in the derivation.
The projection formula is introduced, illustrating the relationship between the surface and ambient spaces.
Exploration of the surface Christoffel symbols in relation to the ambient Christoffel symbols, emphasizing the shift tensor's role.
Discussion on the implications of the ambient space not being Euclidean and its impact on the calculations.
Derivation of the relationship between the surface and ambient Christoffel symbols, including a projection term.
Introduction of the concept of the commutator for tensors with ambient indices, a crucial step towards deriving Gauss's theorem.
Explanation of the shortcut used in the derivation, admitting its limitations but justifying its use for the sake of brevity.
The final expression for the commutator involving the ambient space's Riemann Christoffel tensor, despite the non-Euclidean setting.
The lecturer's determination to reach the derivation of Gauss's theorem, despite the complexity of the calculations.
A pause for board cleaning and strategy explanation, indicating a structured approach to the lecture.
The anticipation of discussing the implications of the theorem beyond the current lecture, such as moving surfaces and relativity.
The lecturer's personal connection to the topic, expressing excitement for the upcoming discussions on related subjects.
Transcripts
Browse More Related Video

Tensor Calculus Lecture 11b: Gauss' Theorema Egregium, Part 2

Tensor Calculus Lecture 8e: The Riemann Christoffel Tensor & Gauss's Remarkable Theorem
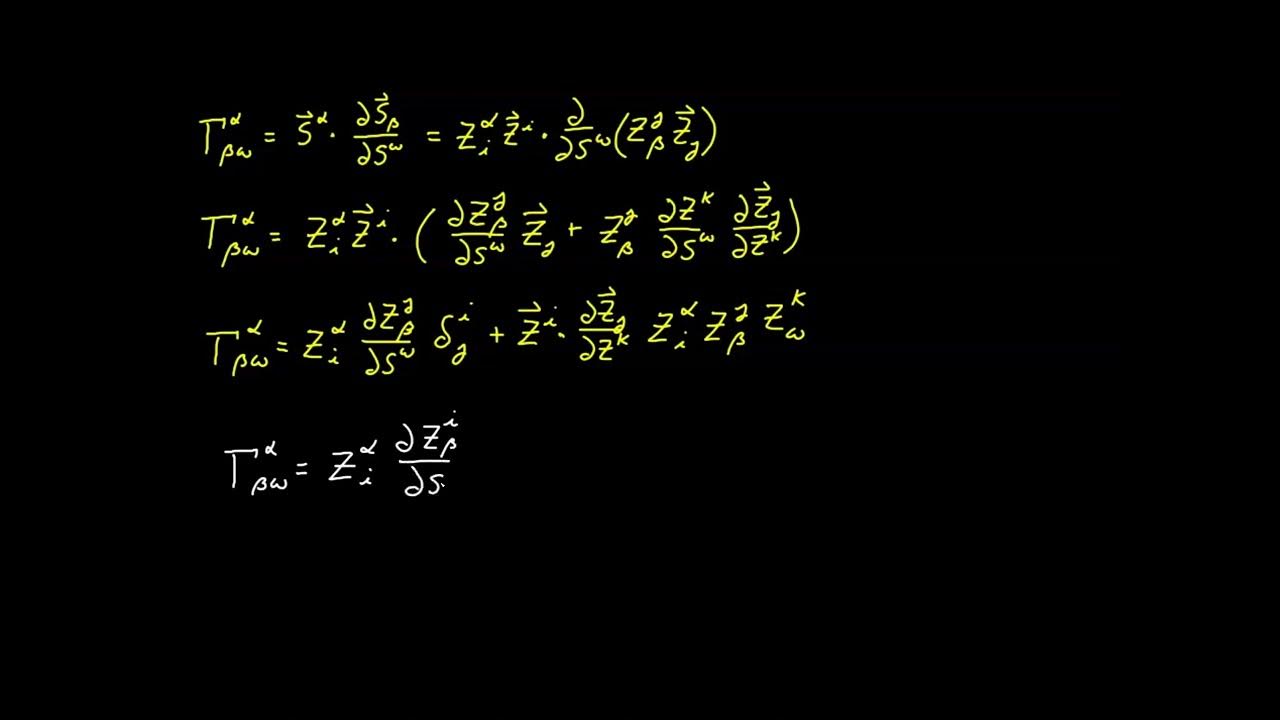
Video 69 - Christoffel Symbol for Surfaces - Part 2

Tensor Calculus 8d: The Christoffel Symbol on the Sphere of Radius R
Tensor Calculus 15: Geodesics and Christoffel Symbols (extrinsic geometry)

The secrets of Einstein's unknown equation – with Sean Carroll
5.0 / 5 (0 votes)
Thanks for rating: