Concavity and the 2nd derivative

Chad Gilliland
7 Oct 201311:41
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains the concept of concavity in calculus, focusing on how the second derivative (F double prime) indicates whether a function is concave up or down. Concave up occurs when F prime is increasing, and concave down occurs when F prime is decreasing. The video also discusses inflection points, where the concavity changes, determined by F double prime equaling zero or changing signs. Through examples and graph analysis, the video demonstrates identifying these properties and how they influence the graph of the function.

Takeaways
  • 📚 Concavity refers to the curvature of a graph and is determined by the sign of the second derivative.
  • 📈 A function is concave up if its first derivative is increasing, and concave down if it is decreasing.
  • 🔍 The second derivative, or F double prime, indicates whether the first derivative is increasing or decreasing.
  • ⚠️ A positive second derivative over an interval means the graph is concave up, while a negative one means it's concave down.
  • 🔄 An inflection point is a point where the concavity of a graph changes, which can be identified when the second derivative is zero or undefined and there's a sign change.
  • 📉 To determine if a function is increasing or decreasing, one can use the first derivative test by setting it to zero and analyzing the intervals.
  • 📊 The first derivative test involves plugging in values from different intervals to see if the derivative is positive (increasing) or negative (decreasing).
  • 📐 Critical points, where the first derivative is zero or undefined, are potential points of extrema (maximum or minimum).
  • 📈 The second derivative test involves setting the second derivative to zero to find potential points of inflection.
  • 🎨 When graphing, one must consider the intervals of increase/decrease, concavity, and the location of extrema and points of inflection to sketch the function accurately.
  • 🖌️ The process of sketching a function involves combining the information about increasing/decreasing intervals, concavity, extrema, and points of inflection to create an accurate visual representation.
Q & A

  • What is the definition of concavity in the context of a function?

    -A function is said to be concave up if its first derivative is increasing on an interval, and concave down if its first derivative is decreasing on an interval.

  • How can you determine if a function is increasing or decreasing?

    -You can determine if a function is increasing or decreasing by examining its first derivative (F prime). If F prime is positive, the function is increasing; if it's negative, the function is decreasing.

  • What does the second derivative (F double prime) indicate about a function?

    -The second derivative indicates whether the first derivative (F prime) is increasing or decreasing. If F double prime is positive, F prime is increasing, and if it's negative, F prime is decreasing.

  • What is an inflection point in a function?

    -An inflection point is a point on the graph of a function where the concavity changes. It occurs where F double prime equals zero or does not exist, and there is a sign change in F double prime or F prime.

  • How can you find the critical points of a function?

    -You can find the critical points of a function by setting its first derivative equal to zero and solving for the variable, which gives you the x-values where the function could have local maxima or minima.

  • What is the first derivative test used for?

    -The first derivative test is used to determine the intervals on which a function is increasing or decreasing by analyzing the sign of the first derivative (F prime) in different intervals around the critical points.

  • How do you find the second derivative of a function?

    -To find the second derivative, you differentiate the first derivative of the function with respect to the variable, which gives you F double prime.

  • What does a positive second derivative indicate about the concavity of a function?

    -A positive second derivative indicates that the function is concave up, meaning it has a 'smile' shape in the region where F double prime is positive.

  • What does a negative second derivative indicate about the concavity of a function?

    -A negative second derivative indicates that the function is concave down, meaning it has a 'frown' shape in the region where F double prime is negative.

  • How can you sketch a graph of a function using the information about its derivatives?

    -You can sketch a graph by identifying key features such as zeros, relative extrema, points of inflection, and the intervals where the function is increasing or decreasing and concave up or down, then drawing the function accordingly.

Outlines
00:00
📚 Understanding Concavity and Inflection Points

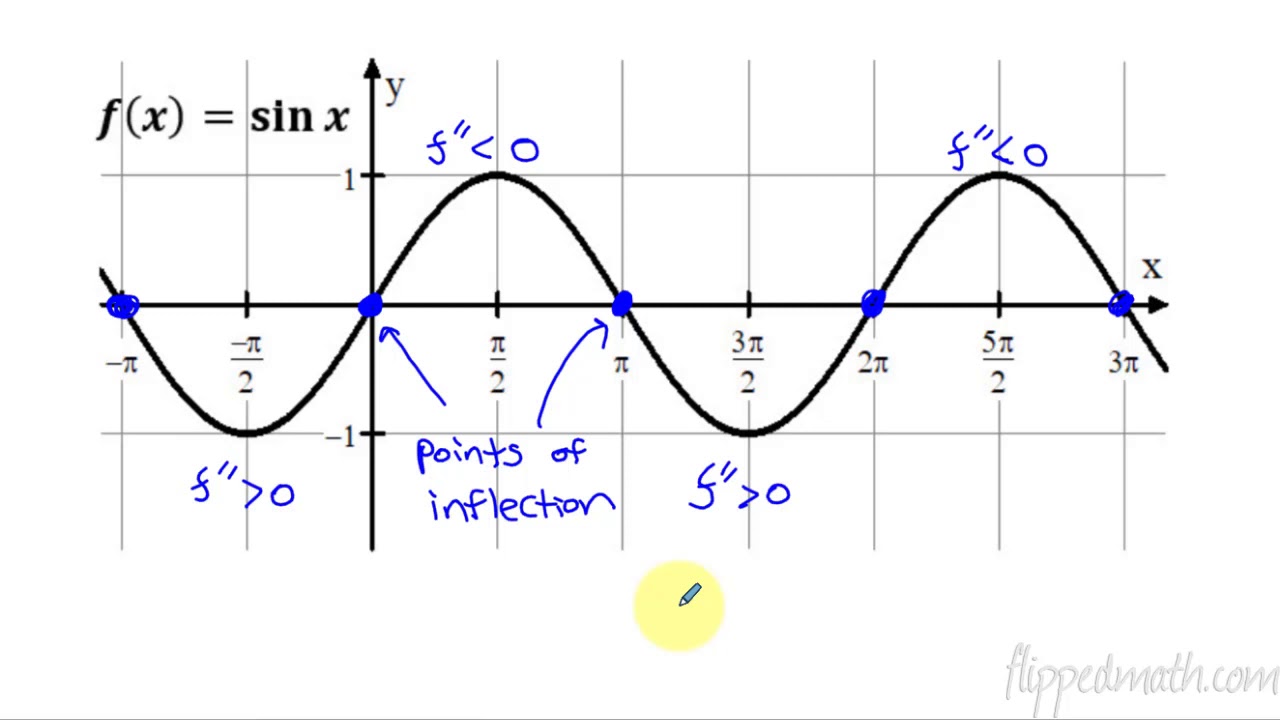
This paragraph introduces the concept of concavity in mathematical functions. It explains that a function is concave up if its first derivative is increasing and concave down if the first derivative is decreasing. The second derivative plays a crucial role in determining the concavity, with a positive second derivative indicating concavity up and a negative one indicating concavity down. The concept of an inflection point is also introduced, which is a point where the concavity of a function changes. The speaker uses a graph to illustrate these concepts, identifying intervals where the function is concave up or down and locating potential inflection points.

05:01
📈 Analyzing Function Behavior with Derivatives

In this paragraph, the focus shifts to analyzing the behavior of a function using its first and second derivatives. The speaker calculates the first derivative of a given function and uses the first derivative test to determine intervals of increase and decrease. A relative minimum is identified at x=3. The second derivative is then calculated, and critical points are found where the second derivative is zero or undefined. These points are potential inflection points. The speaker uses a number line test to determine the concavity of the function in different intervals, identifying points of inflection where the second derivative changes sign.

10:02
🖌️ Sketching Graphs Based on Derivative Analysis

The final paragraph involves sketching graphs based on the analysis of derivatives from the previous paragraphs. The speaker identifies zeros of the original function and uses the information about increasing/decreasing behavior and concavity to sketch the graph. Points of inflection and relative extrema are marked on the graph. The speaker then attempts to sketch two additional graphs based on given conditions, one with a relative maximum and concave down behavior, and another with a sharp turn and concave up behavior. The paragraph concludes with a review of the concepts of points of inflection and concavity.

Mindmap
Keywords
💡Concavity
Concavity refers to the curvature or bending of a graph of a function. In the context of the video, concavity is used to describe whether a function is concave up or concave down. A function is concave up if its graph curves like a smile, and concave down if it curves like a frown. The concept is crucial in understanding the behavior of the function, such as where it might have maxima or minima.
💡Second Derivative
The second derivative, denoted as F'', is the derivative of the first derivative of a function. It is used to determine the concavity of a function. If the second derivative is positive, the function is concave up, and if it is negative, the function is concave down. The video script uses the second derivative to analyze the concavity of a function over different intervals.
💡Increasing/Decreasing
Increasing and decreasing are terms used to describe the behavior of a function's rate of change. A function is increasing if its value gets larger as the independent variable increases, and decreasing if its value gets smaller. In the video, these terms are used to determine the sign of the first derivative, which in turn helps to understand the function's concavity.
💡Inflection Point
An inflection point is a point on the graph of a function where the concavity changes. The video defines an inflection point as a location where the second derivative equals zero or does not exist and the concavity changes from concave up to concave down or vice versa. This concept is important in identifying where the function's curvature changes.
💡First Derivative Test
The first derivative test is a method used to determine the local maxima and minima of a function by analyzing the sign changes of its first derivative. In the video, the first derivative test is applied to find critical points where the function's slope changes from increasing to decreasing or vice versa, indicating potential maxima or minima.
💡Critical Points
Critical points are values of the independent variable where the derivative of a function is zero or undefined. These points are significant as they can indicate local maxima, minima, or points of inflection. The video identifies critical points by setting the first and second derivatives to zero and analyzing the function's behavior around these points.
💡Relative Extrema
Relative extrema refer to the local maxima and minima of a function. In the video, the concept is used to identify points where the function has the highest or lowest values within a certain interval. The first derivative test is used to determine these points by analyzing the sign changes of the first derivative.
💡Tangent Lines
Tangent lines are lines that touch a curve at a single point and have the same slope as the curve at that point. In the video, tangent lines are used to visualize the slopes of the graph, which correspond to the values of the first derivative. This helps in understanding whether the function is increasing or decreasing at different points.
💡Graph Sketching
Graph sketching is the process of drawing a visual representation of a function based on its mathematical properties, such as derivatives and critical points. The video script discusses how to sketch a graph by incorporating information about the function's zeros, relative extrema, points of inflection, and concavity.
💡Undefined Derivative
An undefined derivative indicates a point where the derivative of a function does not exist, typically due to a sharp turn or a vertical asymptote in the graph. In the video, the concept is used to identify points of inflection where the second derivative is undefined, suggesting a change in the function's concavity.
Highlights

Definition of concavity: A function is concave up if its first derivative is increasing on an interval, and concave down if the first derivative is decreasing.

Second derivative (F double prime) determines if the first derivative (F prime) is increasing or decreasing.

If F double prime is positive on an interval, the graph of F is concave up.

If F double prime is negative on an interval, the graph of F is concave down.

Inflection point defined: A function has an inflection point where concavity changes, indicated by F double prime equaling zero or changing sign.

Analyzing slopes of tangent lines to determine if F is increasing or decreasing.

If F prime is negative and increasing, F double prime is positive, indicating concave up.

Finding critical points by setting the first derivative equal to zero and solving for x.

Using the first derivative test to determine intervals of increase and decrease.

Identifying a relative minimum at x=3 where F prime changes from negative to positive.

Setting up the second derivative to analyze concavity changes.

Finding critical points for F prime by setting the second derivative equal to zero.

Using the second derivative test to identify intervals of concave up and concave down.

Identifying points of inflection where F double prime changes sign.

Sketching the graph of F incorporating increasing/decreasing, concavity, and points of inflection.

Practicing graphing functions with given properties like zeros, relative extrema, and concavity.

Transcripts

Browse More Related Video

Graphs of f, f prime, and f double prime

Justifying Points of Inflection on the AP Calculus Exam

What the Second Derivative Tells You about a Graph

Calculus 1: Concavity Examples

MATH1325 Lecture 10 2 - Concavity & Points of Inflection

Calculus AB/BC – 5.6 Determining Concavity of Functions over Their Domains

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusConcavitySecond DerivativeInflection PointsMath TutorialGraph AnalysisCritical PointsMath EducationDerivative TestFunction Behavior