Area Bounded by a Polar Curve

Chad Gilliland
25 Mar 201408:55
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter explores the concept of finding areas within polar graphs, focusing on three examples: a cardioid, a polar rose with three petals, and a graph with four petals. The script begins with a cardioid, explaining the formula for area calculation and demonstrating how to determine the limits of integration. It then delves into the polar rose, highlighting its symmetry and petals, and concludes with a graph of cosine, emphasizing the importance of symmetry in simplifying the area calculation process. Each example is accompanied by a step-by-step guide, including sketching the graphs and setting up integral expressions to find the respective areas.

Takeaways
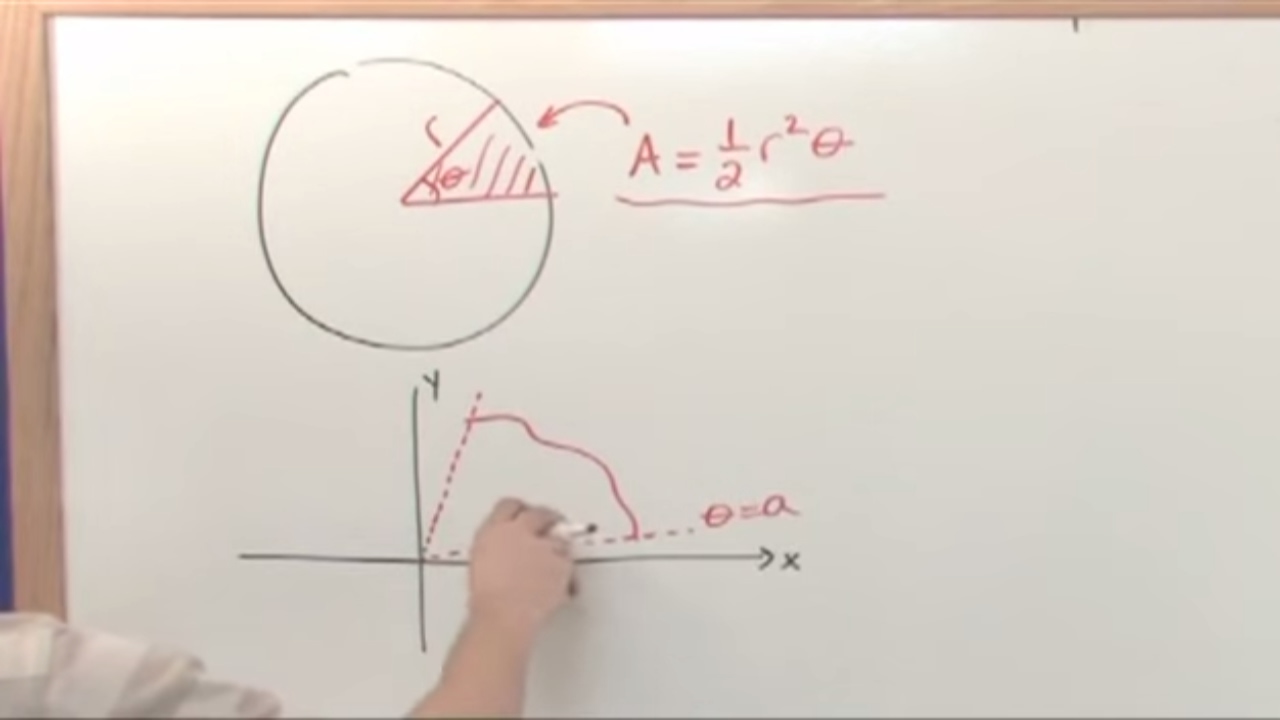
  • 📚 The video script is a tutorial on finding the area within a polar graph by using the formula: area = 1/2 ∫(R^2 dθ) from A to B.
  • 📈 The first example involves a cardioid graph with the equation R = 2 + 2sin(θ), and the area is calculated by integrating from 0 to 2π.
  • 📝 To understand the graph of a cardioid, the instructor suggests making a table of values for θ and R to identify the shape and the limits of integration.
  • 💡 The instructor emphasizes recognizing the cardioid shape from the equation and using symmetry to simplify the area calculation.
  • 🌹 The second example is about finding the area of one petal of a polar rose with the equation R = 2sin(3θ), which has 3 petals due to the sine function's periodicity.
  • 📊 The instructor explains how to determine the start and end of one petal by evaluating the equation at specific angles and using symmetry to calculate the area.
  • 📐 For the polar rose, the instructor uses trigonometric calculations to find the angle at which the radius returns to the pole, which helps in setting up the integral.
  • 🌼 The third example involves a polar graph with the equation R = 4cos(2θ), which is identified as having 4 petals due to the even multiplier of θ.
  • 🔍 The instructor demonstrates how to find the angle at which the radius is zero by setting the equation to zero and solving for θ, which is crucial for the area calculation.
  • 📘 The script concludes with the setup for calculating the area of one petal using the integral from 0 to π/4 of 16cos^2(2θ)dθ, showcasing the use of symmetry and trigonometric identities.
  • 👋 The instructor signs off, indicating that more content will be covered in the next session.
Q & A

  • What is the formula for calculating the area inside a polar graph?

    -The formula for calculating the area inside a polar graph is given by area equals one-half the integral from A to B of R squared d theta.

  • What is a cardioid and how can you identify it from the polar equation?

    -A cardioid is a heart-shaped graph in polar coordinates. It can be identified from a polar equation if the equation has a form like r = a + b * cos(theta) or r = a + b * sin(theta), where a and b are constants.

  • How do you determine the values of A and B for the area calculation formula?

    -The values of A and B are determined by the limits of integration, which correspond to the angles at which the polar graph starts and ends, typically from 0 to 2π for a full graph or a specific range for a partial graph.

  • What is the significance of the sine function in the polar equation r = 2 + 2 * sin(theta)?

    -The sine function in the polar equation r = 2 + 2 * sin(theta) causes the radius to vary with the angle theta, creating a cardioid shape. The amplitude of the sine function (2 in this case) affects the 'height' of the cardioid.

  • How does the graph of r = 2 + 2 * sin(theta) behave at theta = 0, PI/2, PI, and 3PI/2?

    -At theta = 0, the graph is at the point (2, 0). At theta = PI/2, it reaches the maximum radius of 4. At theta = PI, it returns to the radius of 2. At theta = 3PI/2, it is at the pole with a radius of 0.

  • What is the area enclosed by the cardioid r = 2 + 2 * sin(theta)?

    -The area enclosed by the cardioid r = 2 + 2 * sin(theta) is calculated using the integral from 0 to 2π of (2 + 2 * sin(theta)) squared d theta, which evaluates to approximately 18.8496.

  • What is a polar rose and how does the number of petals relate to the equation?

    -A polar rose is a type of polar graph that resembles a flower with multiple petals. The number of petals is determined by the coefficient of theta in the sine or cosine function; if the coefficient is even, the number of petals is twice that coefficient.

  • How do you find the area of one petal of a polar rose with the equation r = 2 * sin(3 * theta)?

    -To find the area of one petal, you can use symmetry and calculate the area from 0 to the angle corresponding to the start of the petal, then double the result. For r = 2 * sin(3 * theta), the area of one petal is found by integrating from 0 to π/6 and doubling the result.

  • What is the significance of the angle 30 degrees in the polar rose with the equation r = 2 * sin(3 * theta)?

    -The angle 30 degrees (or π/6 radians) is significant because it is the starting angle for the first petal of the polar rose. It is derived from the division of 90 degrees by the number of petals (3 in this case).

  • How can you determine the angle at which the radius of a polar graph returns to the pole for the equation r = 4 * cos(2 * theta)?

    -For the equation r = 4 * cos(2 * theta), the radius returns to the pole when the cosine function equals zero. This occurs at angles where 2 * theta is an odd multiple of π/2, specifically at theta = π/4 for the first petal.

  • What is the area of one petal for the polar rose with the equation r = 4 * cos(2 * theta)?

    -The area of one petal for the polar rose with the equation r = 4 * cos(2 * theta) is calculated by integrating from 0 to π/4 of 16 * cos^2(2 * theta) d theta, which gives the area of the upper half of one petal, and then doubling it to account for the full petal.

Outlines
00:00
📐 Understanding Area in Polar Graphs

This section introduces the concept of calculating the area inside a polar graph, specifically using the formula \( \text{Area} = \frac{1}{2} \int_{A}^{B} R^2 d\theta \). The example uses a cardioid, represented by the equation \( R = 2 + 2\sin\theta \), to demonstrate how to determine the values of \( A \) and \( B \), and subsequently calculate the area enclosed by the graph. The process involves creating a table of values for \( \theta \) and \( R \) to understand the shape of the graph and using the formula to find the area.

05:00
🌸 Finding the Area of a Petal in Polar Roses

This part discusses the setup for calculating the area of one petal of a polar rose, using the example \( R = 2\sin(3\theta) \). It explains how to identify key characteristics such as the number of petals and their angles by analyzing the function's periodicity and symmetry. The approach includes determining the limits for integration to find the area of one petal, using symmetry properties to simplify the calculation, and provides a setup for the integral expression without evaluating it.

🌼 Area Calculation for Polar Rose Petals

This section continues with the polar rose example, focusing on \( R = 4\cos(2\theta) \), which has four petals. The explanation includes how to find when the radius returns to zero (the pole), indicating the completion of one petal. The integral setup to find the area of one petal is detailed, utilizing symmetry to simplify the calculation. The description also touches on verifying the angles and the process of squaring the radius function within the integral. This part concludes with an outline of the integral to be solved for the area.

Mindmap
Keywords
💡Polar Graph
A polar graph is a two-dimensional graph of a function in the polar coordinate system, where points are defined by their distance from the pole (origin) and the angle they make with the positive x-axis. In the video, the instructor uses polar graphs to demonstrate how to find areas bounded by certain curves, such as a cardioid and a polar rose.
💡Area
In the context of the video, 'area' refers to the amount of space enclosed within a curve on a polar graph. The formula used to calculate this is integral-based, specifically, area equals one-half the integral from A to B of R squared d theta. The video demonstrates how to apply this formula to different polar functions.
💡Integral
An integral in mathematics is a concept that extends the idea of a sum to a continuous quantity. In the video, the integral is used to calculate the area under the curve of a polar function from one angle to another. The formula involves integrating R squared with respect to theta.
💡Cardioid
A cardioid is a specific type of polar curve defined by the equation r = a(1 + cos θ) or r = a(1 - cos θ), where 'a' is a constant. In the video, the instructor sketches a cardioid using the equation r = 2 + 2 sin θ and calculates its area.
💡Polar Rose
A polar rose is a polar graph that resembles a flower, with multiple petals. The number of petals is determined by the multiple of the angle in the polar equation. In the video, the instructor discusses a polar rose with the equation r = 2 sin 3θ, which has three petals.
💡Theta (θ)
Theta is the angular coordinate in the polar coordinate system, measured in radians or degrees. It represents the angle a point makes with the positive x-axis. In the video, theta is used to define the position on the polar graph and is crucial in calculating areas and setting up integrals.
💡Symmetry
Symmetry in the context of the video refers to the property of a polar graph where the graph is identical on both sides of a certain line or angle. The instructor uses symmetry to simplify the calculation of areas by considering only half or a quarter of the graph and then doubling or quadrupling the result.
💡R Squared
In the formula for calculating the area of a polar graph, R squared refers to the square of the radial distance function. It is the function that, when squared and integrated over an interval of theta, gives the area enclosed by the curve. The video shows how R squared is used in the integral to find areas.
💡Pi (π)
Pi, often denoted as π, is a mathematical constant representing the ratio of a circle's circumference to its diameter. In the video, pi is used in the context of angles measured in radians, particularly when discussing the properties of polar graphs and their integrals.
💡Sine and Cosine
Sine and cosine are trigonometric functions that relate the angles of a right triangle to the lengths of its sides. In the video, these functions are used in the equations of polar graphs (e.g., r = 2 + 2 sin θ and r = 4 cos 2θ) to define the shape of the graph and calculate areas.
Highlights

Introduction to the concept of finding area in a polar graph.

Explanation of the formula for calculating area in polar coordinates: area equals one-half the integral from A to B of R squared d theta.

Demonstration of determining the values of A and B for the integral.

Sketching the graph of 2 + 2 sine theta to find the area bounded by it.

Identification of the graph as a cardioid based on the equation structure.

Method of creating a table of values for theta and R to understand the graph's behavior.

Calculation of the area under the cardioid using the integral formula.

Introduction to the concept of polar roses and their properties, specifically a rose with 3 petals.

Explanation of the angles and symmetry involved in a 3-petal polar rose graph.

Use of symmetry to calculate the area of one petal of the polar rose graph.

Setting up an integral expression to find the area of one petal of a polar rose graph.

Introduction to a polar graph with four petals based on the cosine function.

Explanation of the process to find when the radius of the graph returns to the pole.

Use of trigonometry and algebra to determine the angle at which the radius returns to the pole.

Calculation of the area of one petal using the integral of the squared radius function.

Conclusion and anticipation of further lessons on the topic.

Transcripts

Browse More Related Video

Calculus Polar Area Rose Curve Example

Notes on Polar, Day 3

Lec 33 | MIT 18.01 Single Variable Calculus, Fall 2007

Calculus 2 Lecture 10.5: Calculus of Polar Equations

Lesson 15 - Area And Length In Polar Coordinates (Calculus 2 Tutor)

AP Calculus BC Lesson 9.8

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Polar GraphsArea CalculationIntegralsCardioidPolar RosesTrigonometrySymmetryGraph SketchingMath TutorialEducational Content