How to Prove Trigonometric Identities (Precalculus - Trigonometry 24)
TLDRThe video script is a comprehensive guide on proving trigonometric identities, a topic that can be quite challenging for students. The speaker emphasizes the importance of understanding the thought process behind solving these problems, rather than just plugging in numbers. The video offers a step-by-step approach, starting with identifying the 'harder side' of the identity and working towards simplifying it. Key strategies include looking for obvious identities, simplifying expressions by combining like terms, and transforming trigonometric functions into sines and cosines where beneficial. The speaker also highlights the utility of factoring and the use of difference of squares to simplify complex expressions. Throughout the script, the presenter works through several examples, demonstrating how to apply these techniques to prove various trigonometric identities. The video is designed to equip viewers with a robust set of problem-solving skills that go beyond mere memorization of identities, aiming to foster a deeper understanding of trigonometry.
Takeaways
- 📚 Start with the more complex side of the trigonometric identity and work towards simplifying it to match the simpler side.
- ✅ Look for fractions and try to combine them into a single fraction to simplify the expression.
- 🔍 Identify any obvious trigonometric identities within the expression to leverage in the simplification process.
- 📉 If no immediate identities are apparent, rewrite terms in terms of sine and cosine, which are more versatile for manipulation.
- 🧩 Use known trigonometric identities such as Pythagorean identities, even-odd identities, and reciprocal identities to guide your simplification.
- ➗ When faced with multiple fractions, finding a common denominator can often lead to terms that cancel out, simplifying the expression.
- 🚫 Avoid changing the expression into sines and cosines if an identity is already present, as this can complicate the process.
- 🔢 Always be on the lookout for simplifications and opportunities to use algebraic manipulation to make the expression more manageable.
- ➗ Factoring can be a powerful tool, especially when dealing with expressions that are close to an identity or a difference of squares.
- 👀 Keep the end goal in mind; sometimes restructuring the expression to align with the desired outcome can provide a shortcut to the solution.
- 📉 Remember that proving a trigonometric identity is not about plugging in values but showing that one side is equivalent to the other for all valid angles in the domain.
Q & A
What is the general approach to proving trigonometric identities?
-The general approach involves starting with the more complex side of the identity, looking for simplifications or known identities, rewriting terms in terms of sine and cosine when necessary, and using known trigonometric identities to simplify and prove the identity.
Why is it important to prove trigonometric identities for every valid theta in the domain?
-Proving the identity for every valid theta ensures the identity holds true universally for the given trigonometric functions, not just for specific values of theta.
What is the significance of the Pythagorean identities in proving other trigonometric identities?
-The Pythagorean identities, which relate sine and cosine, form the basis for deriving many other identities. They are often used as a starting point for simplification and are key in proving more complex identities.
How does one decide which side of the identity to start with when proving it?
-One typically starts with the 'harder' side, which is the side that appears more complex or has more terms. This approach helps in systematically breaking down the identity into simpler components.
What is the role of factoring in proving trigonometric identities?
-Factoring is used to simplify expressions and to create opportunities for cancellations or the application of difference of squares, which can lead to the emergence of known identities or a form that matches the other side of the identity being proved.
Why is it recommended to write everything in terms of sine and cosine when no clear identity is apparent?
-Sine and cosine are the fundamental trigonometric functions, and expressing all terms in these functions can often lead to simplifications or the revelation of hidden identities that are not obvious in the original form.
What is the purpose of using the even and odd identities when dealing with negative angles?
-The even and odd identities allow us to relate the values of trigonometric functions at negative angles to their positive counterparts. This is crucial when simplifying expressions involving negative angles and proving identities that hold for all values of theta, including negative angles.
How does the process of making one fraction help in proving identities?
-Combining terms into one fraction can simplify the expression and make it easier to identify common factors, apply identities, or recognize patterns that lead to simplification. It can also help in combining like terms and reducing the overall complexity of the expression.
What is the trick mentioned in the script for handling expressions that are close to an identity?
-The trick involves restructuring the expression to make an existing identity more apparent. This might include factoring out common terms, using the difference of squares, or strategically multiplying by a conjugate to create terms that cancel each other out.
Why is it essential to keep the goal of the proof in mind while working through a trigonometric identity?
-Keeping the goal in mind helps guide the steps taken during the proof. It allows the person proving the identity to make decisions that bring the expression closer to the desired form, using appropriate identities and simplifications that align with the target outcome.
How does the process of proving trigonometric identities help in understanding the underlying mathematics?
-Proving identities is a deep exercise in understanding the relationships between different trigonometric functions and their properties. It reinforces the application of mathematical rules, the use of known identities, and the logical steps required to transform one mathematical expression into another.
Outlines
😀 Introduction to Proving Trigonometric Identities
The video begins with an introduction to the process of proving trigonometric identities, emphasizing the challenges involved. The presenter outlines a general approach to tackling these proofs, noting that while the method may not work every time, it provides a solid starting point. The video promises to walk through 11 examples to demonstrate the application of this method, focusing on modeling thinking patterns and applying common trigonometric identities, such as the Pythagorean identities, throughout the process.
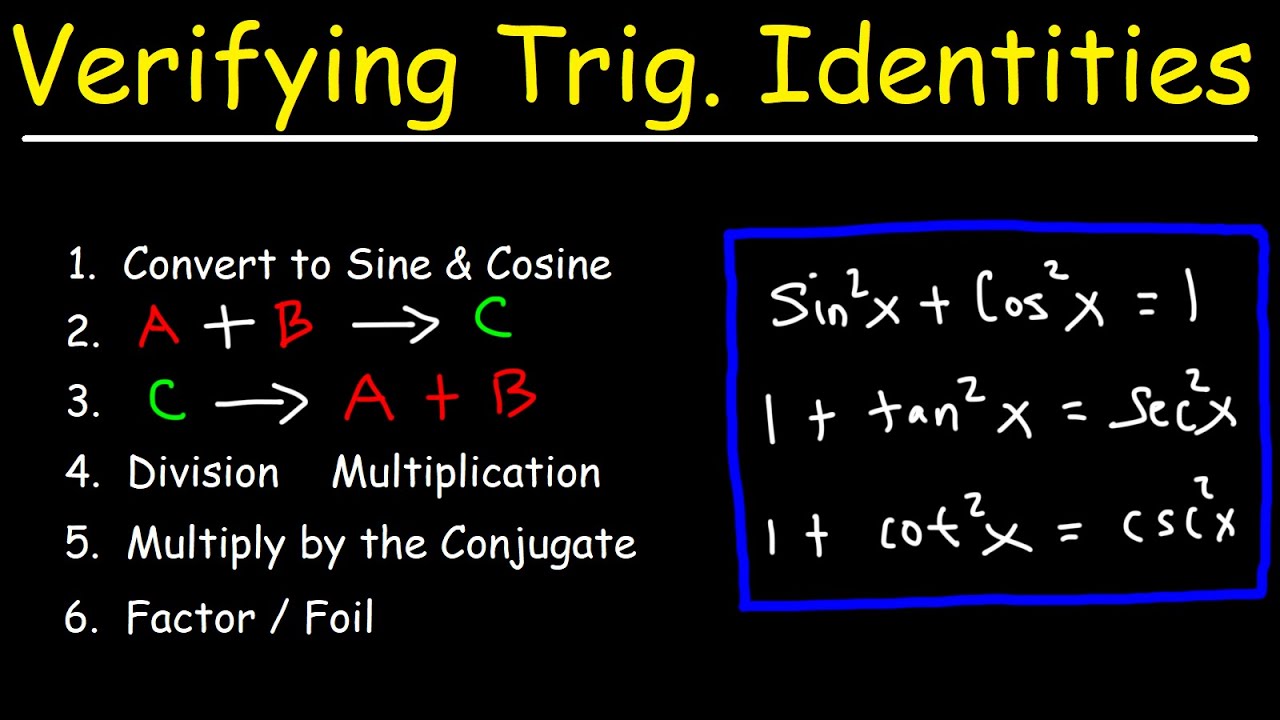
📚 Steps for Proving Trigonometric Identities
The presenter outlines the steps for proving trigonometric identities, which include starting with the more complex side of the equation, looking for fractions and identities, and simplifying expressions using known identities. They stress the importance of writing everything in terms of sine and cosine when no immediate identity is apparent and only using identities that are already known. The video also highlights the thought process behind each step and how to apply them to different examples.
🔍 Identifying and Using Trigonometric Identities
The video script delves into the process of identifying and using trigonometric identities effectively. It emphasizes the importance of recognizing when an identity is close at hand and adapting the proof strategy accordingly. The presenter demonstrates how to simplify expressions and use identities to reach the desired result, such as transforming secant and tangent expressions into sines and cosines or using the Pythagorean identity to simplify terms.
🤔 Approaching Complex Trigonometric Identities
This paragraph discusses the approach to more complex trigonometric identities, encouraging viewers to think critically about the structure of the problem. It highlights the need to consider the goal of the proof and to use known identities to simplify the expression. The presenter also cautions against prematurely converting expressions into sines and cosines, instead suggesting that one should first look for simplifications and identities that are readily apparent.
🧩 Factoring and Simplifying Trigonometric Expressions
The script covers the technique of factoring as a means to simplify trigonometric expressions and make them more manageable. It provides an example where factoring out a term results in a difference of squares, which can then be simplified further. The presenter also discusses the use of identities to transform expressions into a more recognizable form, facilitating the proof process.
📉 Handling Negative Angles in Trigonometric Identities
This section addresses the handling of negative angles within trigonometric functions, using the properties of even and odd functions to simplify expressions. The presenter demonstrates how to use these properties to transform expressions involving negative angles into more familiar forms, which can then be worked with more easily to prove the identity.
🔁 Using Difference of Squares in Trigonometric Proofs
The video script explains the strategy of using the difference of squares to simplify trigonometric expressions. It illustrates how to structure an expression to create two similar terms, which can then be multiplied to form a difference of squares. This technique is particularly useful for canceling out terms in the denominator and reaching the desired form of the identity.
🧠 Critical Thinking in Trigonometric Proofs
The presenter emphasizes the importance of critical thinking in proving trigonometric identities. They note that while there are general steps to follow, each problem may require a different approach. The video encourages viewers to be flexible in their thinking, using identities when they are apparent and simplifying expressions as much as possible to reach the goal of the proof.
📌 Combining Like Terms and Simplifying
The script describes the process of combining like terms and further simplifying trigonometric expressions. It shows how to use known identities, such as the Pythagorean identity, to transform expressions and how to combine terms to reach a simpler form. The presenter also demonstrates the importance of restructuring expressions to make them easier to work with.
🔍 Final Thoughts on Proving Trigonometric Identities
The video concludes with a summary of the steps and strategies for proving trigonometric identities. It reiterates the importance of understanding the process, being able to work with different types of trigonometric expressions, and knowing when to apply various identities. The presenter encourages viewers to practice and develop their own set of strategies for tackling these mathematical challenges.
Mindmap
Keywords
💡Trigonometric identities
💡Proof
💡Hard side
💡Sines and cosines
💡Identity
💡Fractions
💡Distribute
💡Factor
💡Simplify
💡Pythagorean identities
Highlights
The video provides a general method for proving trigonometric identities, which can be challenging, and walks through 11 examples to illustrate the process.
The presenter emphasizes the importance of starting with the 'harder side' of the identity and working towards simplifying it to the 'easier side'.
When faced with multiple fractions, the video suggests simplifying them into a single fraction where possible.
The video advises using known trigonometric identities rather than attempting to derive new ones during the proof process.
The presenter demonstrates how to rewrite trigonometric expressions in terms of sine and cosine to utilize the Pythagorean identities.
The video shows how to use the Pythagorean identity (sine squared theta plus cosine squared theta equals 1) to simplify expressions.
The thought process involves constantly checking for simplifications and known identities while working through each step of the proof.
The video illustrates the technique of distributing and factoring to transform expressions closer to known identities.
The presenter uses the example of secant theta minus 1 over secant theta plus 1 equals tangent squared theta to show the distribution technique.
The video explains how to handle negative angles using even and odd identities for trigonometric functions.
The presenter cautions against prematurely converting everything into sines and cosines, instead recommending the use of existing identities when available.
The video demonstrates the use of difference of squares to simplify fractions and cancel out terms in the denominator.
The presenter shows how to combine like terms and use the goal of the proof to guide the restructuring of expressions.
The video emphasizes the importance of proving identities for all valid theta in the domain of the trigonometric functions, not just for specific values.
The presenter provides a step-by-step guide on how to approach complex proofs, using a combination of algebraic manipulation and trigonometric identities.
The video concludes with a reminder that while there are general steps to follow, proving identities also requires critical thinking and flexibility in approach.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: