Introduction to Using Trigonometric Identities (Precalculus - Trigonometry 23)

Professor Leonard

8 Sept 202123:44

EducationalLearning

32 Likes 10 Comments

TLDRThis video script introduces the concept of trigonometric identities, emphasizing their importance for simplifying complex mathematical problems, particularly in calculus. The speaker outlines basic identities, including reciprocal, Pythagorean, and even-odd identities, and provides a step-by-step approach to simplifying trigonometric expressions. The process involves starting with the more complex side of an equation, combining fractions with a common denominator, and converting all functions into sines and cosines whenever possible. The script also highlights the necessity of using known identities and avoiding unnecessary complications. By simplifying trigonometric functions, students can more efficiently handle challenging mathematical problems, a skill that becomes increasingly valuable as they progress in their studies.

Takeaways

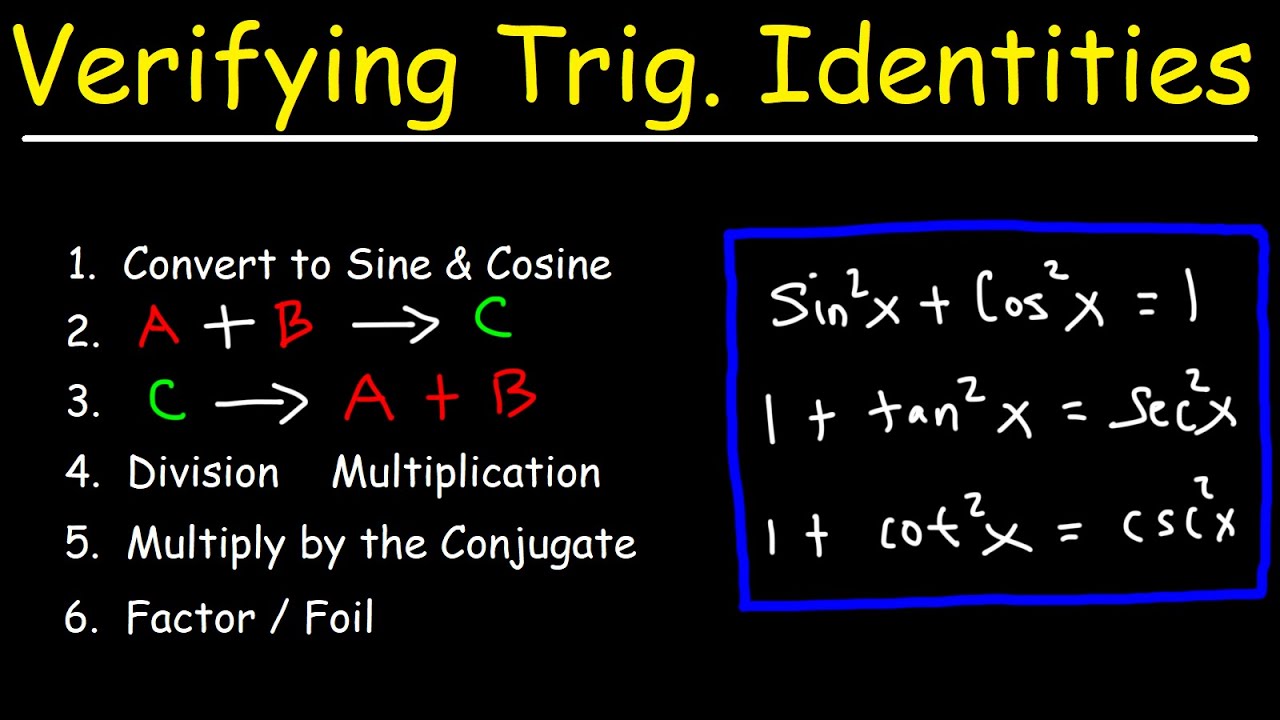
📚 Start by understanding basic trigonometric identities, which are crucial for simplifying expressions and proving more complex identities.
🔄 Know the reciprocal identities, such as tangent being sine over cosine, and the Pythagorean identities like sine squared plus cosine squared equals one.
↔️ Recognize that identities are two-way streets; if one form is true, so is its reciprocal, which is essential for simplifying and proving identities.
➗ When dealing with multiple fractions, aim to combine them into a single fraction with a common denominator.
🔢 Use the Pythagorean identities in various forms, such as tan squared plus one equals secant squared, to manipulate and simplify trigonometric expressions.
🤔 Begin simplifying or proving an identity by starting with the more complex side, which often involves writing everything in terms of sines and cosines.
✅ Always use known identities and avoid making up your own, as they are well-established and will lead to correct simplifications.
🚫 Avoid crossing out terms that are not multiplied together, as this can lead to incorrect simplifications.
🔁 Look for opportunities to factor expressions, especially when everything is in terms of a single trigonometric function like cosine.
📉 Simplify expressions by canceling out common terms in the numerator and denominator, which can significantly reduce the complexity.
🔀 Remember that even and odd functions behave differently with respect to negative angles, which affects how identities are applied.
➡️ The thought process for simplifying or proving identities involves combining fractions, writing in terms of sines and cosines, and using known identities to reach the simplest form.

Q & A

What is the main topic of the video?
-The main topic of the video is trigonometric identities, focusing on their importance, how to use them, and how they can simplify mathematical processes.
Why are trigonometric identities considered useful in calculus?
-Trigonometric identities are considered useful in calculus because they can simplify complex expressions and make dealing with trigonometric functions easier, especially when proving more advanced mathematical concepts.
What are the basic types of trigonometric identities mentioned in the video?
-The basic types of trigonometric identities mentioned in the video are reciprocal identities, Pythagorean identities, and even-odd identities.
How can one use the Pythagorean identities to simplify trigonometric expressions?
-One can use the Pythagorean identities to simplify trigonometric expressions by manipulating the relationships between sine and cosine squared, such as recognizing that sine squared theta plus cosine squared theta equals one.
What is the significance of even and odd identities in trigonometry?
-Even and odd identities in trigonometry are significant because they determine how the function behaves with respect to negative angles. Even functions like cosine and secant yield the same result for both positive and negative angles, while odd functions like sine and tangent yield results that are negatives of each other.
What is the first step suggested in the video for simplifying trigonometric expressions?
-The first step suggested in the video for simplifying trigonometric expressions is to start with the more complex side and use known identities to simplify the expression.
How can one combine multiple fractions in a trigonometric expression?
-One can combine multiple fractions in a trigonometric expression by finding a common denominator, which allows the fractions to be added or subtracted more easily.
What is the purpose of writing everything in terms of sines and cosines when simplifying trigonometric identities?
-Writing everything in terms of sines and cosines simplifies the process because these functions have well-known relationships and identities, making it easier to recognize and apply simplification techniques.
Why is it important to recognize that trigonometric identities are two-way streets?
-It is important to recognize that trigonometric identities are two-way streets because it means that the relationships can be used in both directions, allowing for greater flexibility and efficiency in solving and simplifying trigonometric expressions.
What is the final step suggested in the video for simplifying a trigonometric expression?
-The final step suggested in the video for simplifying a trigonometric expression is to use known identities to write the expression in the most concise form possible, without overcomplicating or expanding it unnecessarily.
What is the advice given in the video for approaching a problem that seems to be getting more complex instead of simpler?
-The advice given in the video for approaching a problem that seems to be getting more complex is to stop and reassess the approach. If the problem is 'exploding' and not simplifying, it might be a sign that a different method or identity should be used.

Outlines

00:00

😀 Introduction to Trigonometric Identities

This paragraph introduces the topic of trigonometric identities and emphasizes their importance in simplifying mathematical problems, especially in calculus. It discusses the basic identities, including reciprocal, Pythagorean, and even-odd identities, and suggests memorizing them for easier application in complex problems. The paragraph also outlines a thought process for simplifying trigonometric expressions using these identities.

05:02

🔍 Simplifying Trigonometric Expressions

The second paragraph delves into the process of simplifying trigonometric expressions. It advises starting with the more complex side of an equation and combining fractions with a common denominator. The paragraph also stresses the importance of converting all functions into sines and cosines and using known identities to simplify the expressions. An example is given to illustrate the process, highlighting the cancellation of terms and the use of reciprocal identities.

10:03

📚 Common Denominators and Factoring

This paragraph focuses on the technique of finding a common denominator for fractions and the importance of factoring in simplifying trigonometric expressions. It warns against the common mistake of incorrectly combining terms and emphasizes the need to distribute terms correctly when combining fractions. The paragraph also demonstrates how to combine terms over a common denominator and simplify using known identities, such as the Pythagorean identity.

15:04

🚫 Avoiding Overcomplication

The fourth paragraph cautions against overcomplicating the simplification process. It advises using known identities and not creating new ones. The paragraph also discusses the possibility of simplifying expressions by factoring, especially when all terms are in cosine form. An example is provided to show how factoring can lead to a more concise form of the expression, avoiding unnecessary complexity.

20:05

🔄 Recap and Future Topics

The final paragraph recaps the strategies for simplifying trigonometric identities, including using the more complex side, writing everything in terms of sines and cosines, and factoring when possible. It also teases the next video, which will cover more advanced identities and proofs, promising a step-by-step guide with many examples.

Mindmap

Keywords

💡Trigonometric Identities

Trigonometric identities are mathematical equations involving trigonometric functions that hold true for every value of the variable. They are essential in simplifying trigonometric expressions and proving other trigonometric identities. In the video, the speaker discusses the importance of these identities in making calculations easier, especially in higher-level mathematics like calculus.

💡Even and Odd Functions

Even functions are symmetric with respect to the y-axis, meaning that f(x) = f(-x), while odd functions are symmetric with respect to the origin, meaning that f(x) = -f(-x). The video explains that cosine and secant are even functions, and all other trigonometric functions are odd, which is crucial for understanding how the values of these functions change with the input angle.

💡Pythagorean Identities

Pythagorean identities are a set of trigonometric identities that relate the squares of sine and cosine functions to 1. The most common is sin²θ + cos²θ = 1. These identities are fundamental in trigonometry and are used in the video to demonstrate how to manipulate trigonometric expressions and simplify them.

💡Reciprocal Identities

Reciprocal identities in trigonometry state that the reciprocal of a trigonometric function is equal to a different trigonometric function. For example, cotangent is the reciprocal of tangent (cot(θ) = 1/tan(θ)), and secant is the reciprocal of cosine (sec(θ) = 1/cos(θ)). The video emphasizes their importance in transforming expressions into more manageable forms.

💡Simplification

Simplification in the context of trigonometry refers to the process of making trigonometric expressions easier to work with by using identities to reduce complexity. The video script provides a detailed approach to simplifying expressions like tan(θ) * csc(θ) by converting them into sines and cosines and then applying identities to reach a more concise form.

💡Common Denominator

A common denominator is a single denominator that can be used for all terms in a fraction, especially when adding or subtracting fractions with different denominators. In the video, the speaker illustrates how to use a common denominator to combine fractions, which is a crucial step in simplifying complex trigonometric expressions.

💡Factoring

Factoring is an algebraic method used to express an expression as the product of its factors. In the context of the video, factoring is applied to trigonometric expressions to simplify them. For example, the difference of squares, such as cos²θ - 1, can be factored into (cosθ - 1)(cosθ + 1), making the expression easier to work with.

💡Sine and Cosine Functions

Sine (sin) and cosine (cos) are the two primary trigonometric functions that are used in the video to demonstrate various identities and simplification techniques. They are fundamental to trigonometry and are often used as the basis for expressing other trigonometric functions due to their versatility and the numerous identities associated with them.

💡Secant and Cosecant Functions

Secant (sec) and cosecant (csc) are reciprocal trigonometric functions. Secant is the reciprocal of cosine, and cosecant is the reciprocal of sine. The video discusses their identities and how they can be used to simplify expressions by converting them into sines and cosines or vice versa.

💡Tangent and Cotangent Functions

Tangent (tan) and cotangent (cot) are also reciprocal trigonometric functions, where tangent is the ratio of sine to cosine, and cotangent is the ratio of cosine to sine. The video emphasizes their reciprocal identities and how they can be represented in terms of sine and cosine to facilitate the simplification of trigonometric expressions.

💡Algebraic Techniques

Algebraic techniques such as combining like terms, distributing, and factoring are essential in simplifying trigonometric expressions. The video demonstrates how these techniques, which are common in algebra, can be applied to trigonometric identities to achieve a more straightforward form, making them easier to understand and work with.

Highlights

Introduction to trigonometric identities and their importance in simplifying mathematical problems.

Explanation of basic trigonometric identities, including reciprocal, Pythagorean, and even-odd identities.

The significance of understanding identities for tackling more complex problems in calculus.

Strategy for simplifying trigonometric expressions by combining fractions and using known identities.

Demonstration of converting tangent and cosecant into sines and cosines for simplification.

Use of the Pythagorean identity to simplify expressions involving sine and cosine squared.

Technique for changing everything into sines and cosines when stuck on an identity.

Emphasis on the two-way nature of identities and their flexible application in problem-solving.

Approach to simplifying complex fractions by finding a common denominator.

The process of factoring as a method to simplify trigonometric expressions, especially when everything is in terms of cosine.

Warning against overcomplicating problems by incorrectly applying identities or algebraic maneuvers.

Example of simplifying an expression involving sine and cosine by factoring and using identities.

Advice on when to stop and reassess if a problem is becoming overly complex instead of simplifying.

The importance of recognizing when an expression is already simplified and not overmanipulating it.

Strategy for simplifying by writing everything in terms of sines and cosines and then applying factoring techniques.

Final recap of the steps for simplifying trigonometric identities and the importance of using known identities.

Preview of future videos covering more advanced identities and proofs with step-by-step examples.

Transcripts

Browse More Related Video

Tips to verifying trigonometric identities

Pythagorean Identities for Trigonometric Functions (Precalculus - Trigonometry 10)

How to Prove Trigonometric Identities (Precalculus - Trigonometry 24)

Verifying Trigonometric Identities

Proving Trigonometric Identities | Fundamental Trigonometric Identities | Formulas | Sample Problems

Rational Expressions Review

Related Tags

Trigonometric Identities Math Simplification Sine Cosine Pythagorean Reciprocal Even Odd Functions Fractions Algebraic Techniques Trigonometry Basics Calculus Preparation Educational Content