Ch. 2.4 Average Rate of Change of A Function
TLDRThis pre-calculus video explores the concept of the average rate of change of a function, highlighting its relation to the slope of a line but emphasizing its broader application to non-linear functions. The instructor explains how to calculate the average rate of change using function notation and provides a real-world example involving a rock thrown from a cliff. The video demonstrates the process of determining the average change in height over a specific horizontal distance, using a quadratic function to model the projectile motion and concluding with the calculation of the average rate of descent.
Takeaways
- 📚 The video discusses the concept of the average rate of change of a function, which is closely related to the slope of a line but applicable to non-linear functions as well.
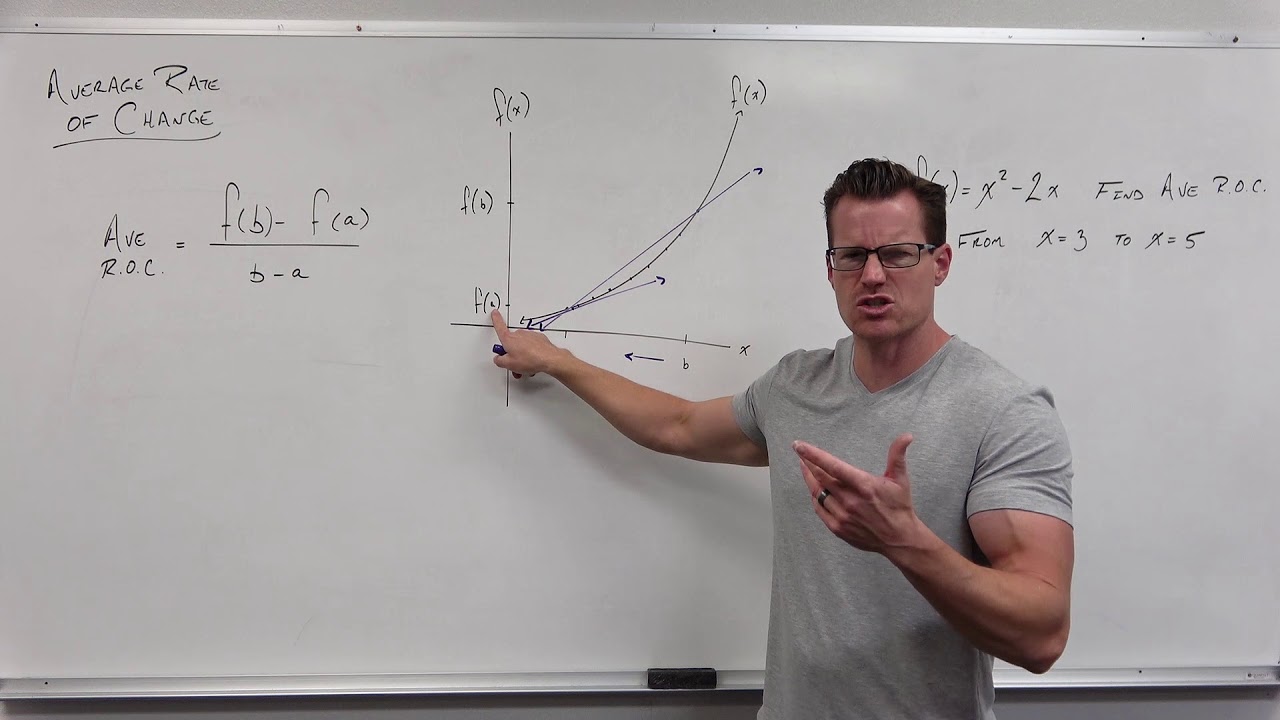
- 📉 The slope of a line (m) is defined as the difference in outputs over the difference in inputs, which can be represented as \( \frac{f(x_1) - f(x_0)}{x_1 - x_0} \) in function notation.
- 🔍 When a function is not linear, the average rate of change represents the slope of a secant line, which connects two points on a curve.
- 📈 The average rate of change is useful for understanding how a function changes on average over an interval, even if the function is increasing and decreasing within that interval.
- 📏 For linear functions, the average rate of change is constant and equal to the slope of the function, as it increases or decreases at a steady pace.
- 🚀 The video provides an example involving a rock thrown off a cliff, which is a practical application of calculating the average rate of change.
- 📊 The example involves calculating the average change in height of the rock from 10 feet to 50 feet from the point it was thrown, using the given distances and heights.
- 🧩 To solve the example, a quadratic model of the rock's trajectory is needed, which can be determined using the known x-intercepts and the maximum height.
- 🔢 The general form of the quadratic function is derived from the x-intercepts and the vertex, and the value of 'a' is calculated to complete the function.
- ✂️ The function is then used to find the outputs at the specified inputs (10 feet and 50 feet from the throw point) to determine the net change in height.
- 📉 Finally, the average rate of change in height is calculated by dividing the net change in height by the horizontal distance, yielding the average decrease in height per unit of distance.
Q & A
What is the main topic of the video?
-The main topic of the video is the concept of the average rate of change of a function, which is closely related to the slope of a line but applies to non-linear functions as well.
What is the formula for the slope of a line in terms of function notation?
-The formula for the slope of a line in terms of function notation is given by \(m = \frac{f(x_1) - f(x_0)}{x_1 - x_0}\), where \(f(x)\) is the function, \(x_0\) and \(x_1\) are the inputs, and \(f(x_0)\) and \(f(x_1)\) are the corresponding outputs.
What is a secant line in the context of this video?
-A secant line is a line that connects two points on a curve, representing the average rate of change of the function between those two points.
How does the video explain the concept of the net change in the context of average rate of change?
-The net change is explained as the difference in the outputs of the function at two different points, which is the total change in height of the function from one point to another.
What is the example problem presented in the video?
-The example problem involves a rock being thrown off a 100-foot cliff, with the goal of finding the average change in height of the rock from 10 feet to 50 feet from where it was thrown.
What is the significance of the maximum height of the rock in the example problem?
-The maximum height of the rock, which is 30 feet above the cliff, is used to determine the quadratic function that models the projectile motion of the rock.
How does the video suggest finding the equation of the quadratic function for the rock's motion?
-The video suggests using the known x-intercepts and the maximum height to determine the equation of the quadratic function, which can then be used to find the average rate of change.
What is the purpose of finding the average rate of change in the example problem?
-The purpose is to determine how the height of the rock changes on average as it travels from 10 feet to 50 feet from the point it was thrown.
How does the video handle the calculation of the average rate of change for the rock's motion?
-The video demonstrates the calculation by plugging in the specific x-values (10 and 50 feet) into the derived quadratic function to find the corresponding y-values (heights), and then calculating the average rate of change using these values.
What is the final step in solving the example problem in the video?
-The final step is to calculate the average rate of change by dividing the net change in height by the horizontal distance the rock travels between the two points.
Outlines
📚 Introduction to Average Rate of Change
This paragraph introduces the concept of the average rate of change of a function, relating it to the slope of a line but emphasizing its broader application to non-linear functions. The instructor explains the transition from discussing the slope of a line to the average rate of change by using function notation, where the slope is represented as the difference in outputs (f(x1) - f(x0)) over the difference in inputs (x1 - x0). The concept of a secant line, which connects two points on a curve, is introduced as a means to calculate the average rate of change between those points, highlighting its importance in calculus.
🚀 Application of Average Rate of Change in Projectile Motion
The second paragraph presents an application problem involving the average rate of change in the context of projectile motion. The scenario describes a rock being thrown off a 100-foot cliff by a 6-foot tall person, reaching a maximum height of 30 feet above the cliff at a point 20 feet away from the throw point, and landing 70 feet away in the water. The task is to calculate the average change in the rock's height from 10 feet to 50 feet away from the throw point. The instructor outlines the problem, emphasizing the need to visualize and label the key points on a graph to understand the distances and heights involved.
🔍 Deriving the Quadratic Model for Projectile Motion
In this paragraph, the focus shifts to deriving the quadratic equation that models the projectile motion described in the problem. The instructor uses the given information about the projectile's trajectory, including the maximum height and the points where the rock lands in the water, to determine the x-intercepts of the parabola. The process involves understanding the symmetry of the parabola and using the zero at x = 70 to find the other x-intercept at x = -30. The instructor then formulates the general form of the quadratic function and solves for the leading coefficient 'a' using the zero at x = 70 and the height at that point.
📉 Calculating the Average Rate of Change Using the Quadratic Model
The final paragraph details the calculation of the average rate of change in the rock's height from 10 feet to 50 feet away from the throw point using the derived quadratic model. The instructor demonstrates how to plug in the specific x-values into the quadratic function to find the corresponding y-values (heights). The net change in height is then divided by the horizontal distance to obtain the average rate of change. The summary emphasizes the importance of maintaining exact values throughout the calculation to avoid decimal approximations and ensure precision in the final result.
Mindmap
Keywords
💡Average Rate of Change
💡Slope
💡Function Notation
💡Secant Line
💡Net Change
💡Quadratic Function
💡Projectile Motion
💡Parabola
💡X-Intercept
💡Y-Intercept
Highlights
Introduction to the concept of average rate of change in the context of pre-calculus.
Explaining the relationship between average rate of change and the slope of a line.
Clarifying the difference between functions and linear equations in terms of slope calculation.
Transitioning from point notation to function notation for discussing slope.
Introducing the concept of a secant line and its relevance to calculus.
Describing the process of finding the slope of a secant line using function notation.
Differentiating between the slope of a function and the slope of a secant line.
Illustrating the calculation of average rate of change with an example of a parabola.
Using a real-world scenario of a rock thrown off a cliff to demonstrate average rate of change.
Setting up the problem with given distances and heights to find the average change in height.
Drawing a visual representation to understand the problem and identify key points.
Identifying the need for a mathematical model to find unknown outputs for average rate of change.
Deriving the quadratic function model for the projectile motion using given points.
Calculating the average rate of change using the derived quadratic function.
Emphasizing the importance of using exact values in calculations to avoid approximation errors.
Final calculation of the average rate of change in height of the rock during its trajectory.
Conclusion summarizing the findings and the application of average rate of change in the given example.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: