Calculus - Order and Degree of a Differential Equation | Don't Memorise

Infinity Learn NEET
26 Jul 202105:31
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces the fundamental concepts of differential equations, focusing on the differentiation of functions with respect to an independent variable. It explains the process of finding the derivative of a function, exemplified by y = x^2, and then delves into the definitions of order and degree in the context of differential equations. The script provides clear examples to illustrate these concepts, emphasizing that the degree is only defined for polynomial equations in derivatives. The video promises to solve examples in the next installment to deepen the understanding of these mathematical principles.

Takeaways
  • 📘 Differentiation is the process of finding the derivative of a function with respect to an independent variable.
  • 🔢 For example, the derivative of y = x^2 is given by dy/dx = 2x.
  • 📊 A differential equation involves variables and derivatives of the dependent variable with respect to the independent variable.
  • 📝 There are two key concepts in differential equations: order and degree.
  • 📈 The order of a differential equation is the order of the highest order derivative of the dependent variable with respect to the independent variable.
  • 📉 Example: For d^3y/dx^3 = f(x), the order is 3.
  • 🔍 The degree of a differential equation is the highest power of the highest order derivative involved, provided the equation is a polynomial in derivatives.
  • 🔢 Example: For (d^3y/dx^3)^1 = f(x), the degree is 1.
  • ⚠️ The degree is only defined if the differential equation can be written as a polynomial equation in derivatives.
  • 📚 Understanding these concepts of order and degree helps in classifying and solving differential equations more effectively.
Q & A

  • What is the derivative of the function y = x^2 with respect to x?

    -The derivative of y with respect to x, denoted as dy/dx, is 2x.

  • What is a differential equation?

    -A differential equation is an equation that involves derivatives of the dependent variable with respect to the independent variable.

  • What is meant by the 'order' of a differential equation?

    -The order of a differential equation is the order of the highest derivative of the dependent variable with respect to the independent variable in the equation.

  • What is the order of the differential equation involving the third derivative of y?

    -The order of the differential equation involving the third derivative of y is three.

  • What is the order of a differential equation with the highest derivative being the second derivative?

    -The order of a differential equation with the highest derivative being the second derivative is two.

  • What is the degree of a differential equation?

    -The degree of a differential equation is the highest power of the highest order derivative involved in the equation, provided the equation is a polynomial in derivatives.

  • Is the degree of a differential equation always defined?

    -No, the degree of a differential equation is only defined if the equation is a polynomial in derivatives.

  • What is the degree of the differential equation d^3y/dx^3 = 1?

    -The degree of the differential equation d^3y/dx^3 = 1 is one, as the highest order derivative is to the power of one.

  • How is the degree of a differential equation determined when there are multiple terms with the same highest order derivative but different powers?

    -The degree of a differential equation is determined by the highest power of the highest order derivative present in the equation.

  • Why might the degree of a differential equation not be defined in some cases?

    -The degree of a differential equation might not be defined if the equation is not a polynomial in derivatives, meaning it does not involve terms raised to powers.

  • What is the significance of understanding the order and degree of a differential equation?

    -Understanding the order and degree of a differential equation is crucial for classifying the equation and determining the appropriate methods for solving it.

Outlines
00:00
📚 Introduction to Differential Equations

This paragraph introduces the concept of differentiation of a function with respect to an independent variable, using the example of y = x^2. It then explains the formation of a differential equation, which includes the derivative of the dependent variable y with respect to the independent variable x. The paragraph further delves into the fundamental concepts of 'order' and 'degree' in differential equations, illustrating them with examples. The order is defined as the highest order of the derivative present in the equation, while the degree is the highest power of that derivative, provided the equation is a polynomial in derivatives.

05:03
🔍 Understanding Order and Degree Further

Building upon the initial explanation, this paragraph continues to explore the order and degree of differential equations, emphasizing the importance of polynomial form for the degree to be defined. It provides examples to clarify the concepts, showing how to identify the order by looking at the highest derivative in the equation and how to determine the degree by examining the highest power of that derivative. The paragraph also points out that if an equation is not a polynomial in derivatives, the degree is not defined, as illustrated with a non-polynomial example.

Mindmap
Keywords
💡Differentiation
Differentiation is the process of finding the derivative of a function with respect to an independent variable. In the video, differentiation of y = x^2 is shown, resulting in dy/dx = 2x. This concept is fundamental for understanding changes in functions and is a precursor to discussing differential equations.
💡Function
A function is a mathematical relationship where each input (independent variable) is related to exactly one output (dependent variable). The video uses the function f(x) = x^2 to explain differentiation and later transition into differential equations by expressing the function as y = x^2.
💡Independent Variable
An independent variable is the variable that is manipulated or changed in an equation to observe its effect on the dependent variable. In the video, x is the independent variable in the function y = x^2. Understanding this concept is crucial as it forms the basis of how functions and their derivatives are analyzed.
💡Dependent Variable
A dependent variable is the variable that depends on the independent variable. In the function y = x^2 discussed in the video, y is the dependent variable because its value changes according to x. This concept is essential for comprehending how changes in one variable affect another.
💡Derivative
A derivative represents the rate of change of a function with respect to a variable. The video introduces derivatives by showing dy/dx = 2x for the function y = x^2. Derivatives are central to understanding differential equations, as they involve rates of change and slopes of curves.
💡Differential Equation
A differential equation is an equation that involves derivatives of a dependent variable with respect to an independent variable. The video explains that such equations describe how variables change and introduces the concept by differentiating y = x^2. Differential equations are used to model various physical phenomena and are crucial in mathematics.
💡Order of Differential Equation
The order of a differential equation is the order of the highest derivative present in the equation. The video explains this with examples, showing that an equation with a third-order derivative has an order of three. Understanding the order helps classify differential equations and predict their complexity.
💡Degree of Differential Equation
The degree of a differential equation is the highest power of the highest order derivative, provided the equation is polynomial in derivatives. The video illustrates this concept by showing equations with degrees of one and two. The degree helps in understanding the behavior and solutions of differential equations.
💡First-Order Derivative
A first-order derivative is the derivative of a function taken once with respect to a variable. The video shows this by differentiating y = x^2 to get dy/dx = 2x. First-order derivatives represent the initial rate of change and are the simplest form of derivatives in differential equations.
💡Second-Order Derivative
A second-order derivative is the derivative of a first-order derivative, indicating how the rate of change itself changes. In the video, this is shown by differentiating dy/dx = f'(x) again to get d^2y/dx^2 = f''(x). Second-order derivatives are important in understanding the curvature and acceleration of functions.
Highlights

Introduction to differentiation of a function with respect to an independent variable.

Differentiation of the function f(x) = x^2 results in dy/dx = 2x.

Explanation of differential equations involving derivatives of dependent variables with respect to independent variables.

Differential equations are defined by the order and degree of their highest derivative.

Order of a differential equation is the highest order of its derivative.

Example provided to illustrate the concept of order in differential equations.

Degree of a differential equation is the highest power of its highest order derivative.

The degree is only defined for polynomial differential equations in derivatives.

Examples given to demonstrate how to determine the degree of a differential equation.

Clarification on why the degree is not defined for non-polynomial differential equations.

Differentiation process explained for finding first and second order derivatives.

Importance of understanding both order and degree for classifying differential equations.

Differentiation of a function y = f(x) leads to dy/dx = f'(x), indicating a first order derivative.

Further differentiation results in d²y/dx² = f''(x), known as a second order derivative.

A differential equation with the highest order derivative of 3 is classified as third order.

A differential equation with the highest order derivative of 2 is classified as second order.

A differential equation with the highest order derivative of 1 is classified as first order.

Upcoming video promises to solve examples for a deeper understanding of differential equations.

Transcripts

Browse More Related Video

Order and Degree of Differential Equations | Differential Equations #order #degree #differential

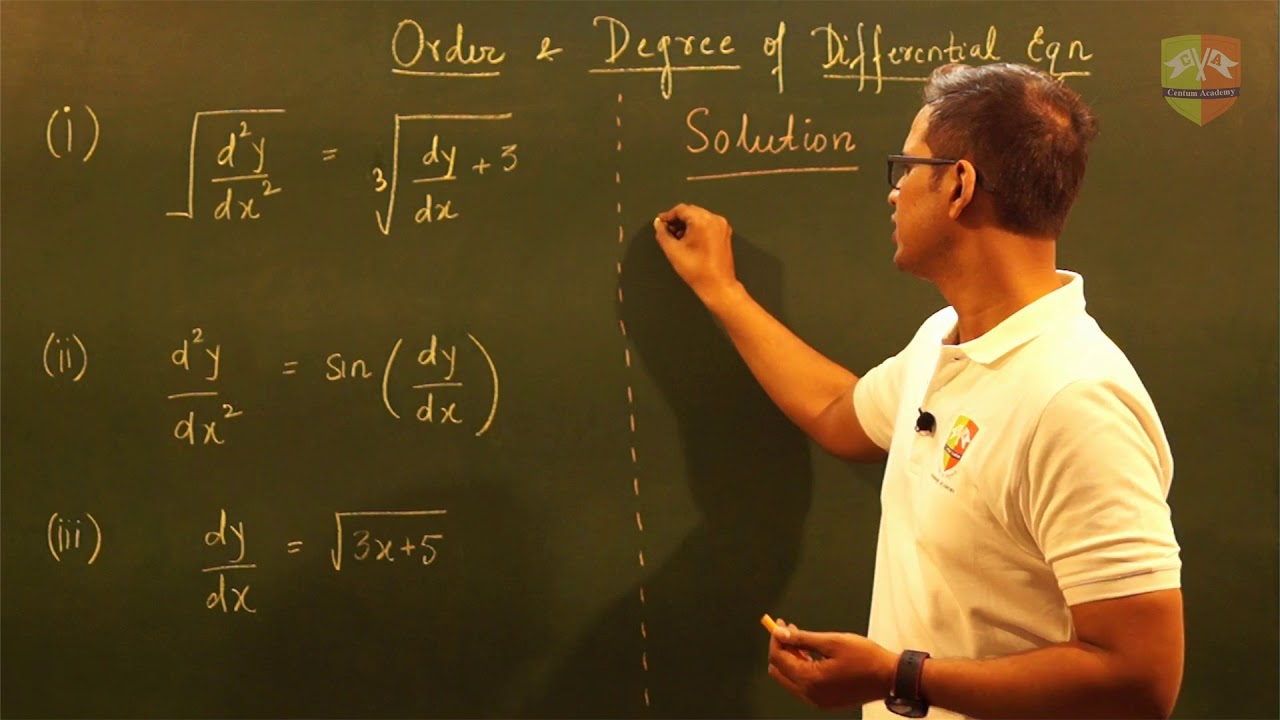
Differential Equations - Introduction - Part 1

Implicit Differentiation Second Derivative Trig Functions & Examples- Calculus

BusCalc 14.3 Extrema of Multivariable Functions

Differential Equations with Velocity and Acceleration (Differential Equations 7)

Implicit Differentiation Day 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Differential EquationsMathematicsEducationalDerivativesOrder ConceptDegree ConceptPolynomial EquationsFirst OrderSecond OrderConcept Clarification