Calculus 3: Maximum and Minimum Values (Video #17) | Math with Professor V

Math with Professor V

19 Jun 202065:34

EducationalLearning

32 Likes 10 Comments

TLDRThis calculus video lecture delves into finding maximum and minimum values of functions involving multiple variables. It revisits the process for single-variable functions, emphasizing critical values and derivative tests. The lesson then transitions to multivariable functions, introducing the D-test for local extrema and strategies for absolute extrema on closed regions. Practical applications, such as maximizing box volume and minimizing distances between parallel planes, demonstrate the utility of these concepts in real-world problems.

Takeaways

📚 The lecture introduces the concept of finding maximum and minimum values for functions of several variables, beginning with a review of the process for functions of one variable.
🔍 Critical values for single-variable functions are identified by either setting the first derivative equal to zero or where the derivative does not exist.
📈 The first derivative test involves analyzing the sign of the derivative around critical points to determine if a relative maximum or minimum is achieved.
📉 The second derivative test is used to assess local extrema by evaluating the concavity of the function at critical points through the second derivative.
🔑 For functions of several variables, critical points are found where partial derivatives with respect to each variable are zero or undefined simultaneously.
📐 The D-test is a method used for functions of several variables to determine the nature of critical points by evaluating a specific quantity involving second partial derivatives.
📈 The criteria for the D-test involve comparing the sign of the defined quantity D and the second partial derivative with respect to one of the variables to classify relative maxima, minima, or saddle points.
🔍 When the second derivative test is inconclusive, the first derivative test is used as an alternative method to determine the nature of critical points.
📘 The script provides step-by-step examples to demonstrate the process of finding critical points, applying the D-test, and determining the nature of extrema for functions of two variables.
🔄 The process for absolute extrema involves considering critical points within a closed region and on its boundary, ensuring all potential extrema are evaluated.
🎯 The lecture concludes with applications of optimization, such as finding the maximum volume of a box with a face in a given plane and the shortest distance between parallel planes, using the concepts of critical points and extrema.

Q & A

What is the main topic of this calculus video lecture?
-The main topic of this calculus video lecture is finding maximum and minimum values for functions of several variables.
How are critical values for a function of one variable found?
-Critical values for a function of one variable are found by either setting the first derivative equal to zero or identifying points where the derivative does not exist.
What are the two tests mentioned for confirming whether a critical value is a relative maximum or minimum for a function of one variable?
-The two tests mentioned are the first derivative test and the second derivative test.
How does the first derivative test work for a function of one variable?
-The first derivative test involves creating a number line with the values of the first derivative and identifying the behavior of the function around the critical value to determine if it is a relative maximum or minimum.
What is the purpose of the second derivative test for local extrema?
-The second derivative test is used to determine if the function is concave up or down at the critical point, which helps in identifying whether the point is a relative minimum or maximum.
What is the condition for a critical point in a function of two variables?
-A critical point in a function of two variables occurs where both the partial derivative with respect to x and the partial derivative with respect to y are simultaneously zero or either of them is undefined.
What is the D test used for in functions of several variables?
-The D test is used to determine whether a critical point in a function of several variables is a relative maximum, minimum, or saddle point.
What is the condition for the D test to be applicable?
-The D test is applicable when the second partial derivatives of the function are continuous on a disk centered at the critical point and the partial derivatives with respect to each variable at the critical point are zero.
What is a saddle point in the context of functions of several variables?
-A saddle point is a critical point in a function of several variables where the function neither achieves a relative maximum nor minimum, and its behavior can be viewed as a minimum or maximum from different perspectives.
What is the process for finding absolute extrema for a function of a single variable on a closed interval?
-The process involves finding critical points, considering the endpoints of the interval, evaluating the function at these points, and then identifying the largest and smallest function values as the absolute maximum and minimum, respectively.
How does the process differ for finding absolute extrema for a function of several variables on a closed region?
-For functions of several variables, the process includes finding critical points within the region, identifying potential extreme values on the boundary of the region, checking corner points where boundary equations intersect, and evaluating the function at these points to determine the absolute extrema.
What is an example of an application problem involving optimization that could be solved using the concepts discussed in the lecture?
-An example application problem could be finding the dimensions of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex on a given plane, which involves maximizing the volume of the box.
What is the shortest distance between two parallel planes and how can it be found?
-The shortest distance between two parallel planes can be found by considering a point on one plane and connecting it to an arbitrary point on the other plane, then minimizing the squared distance between these points, which avoids dealing with square roots and simplifies the calculation.
What is the significance of the extreme value theorem in the context of absolute extrema for functions of several variables?
-The extreme value theorem guarantees that if a function is continuous on a closed and bounded region, then it attains both an absolute maximum and an absolute minimum value within that region.

Outlines

00:00

📚 Calculus Lecture on Maxima and Minima

This paragraph introduces a calculus lecture focused on finding maximum and minimum values of functions involving multiple variables. It begins with a review of the process for single-variable functions, emphasizing the identification of critical points through the first derivative test and the second derivative test. The first derivative test involves analyzing the sign changes of the derivative around critical points, while the second derivative test relies on the concavity of the function at those points. The lecture then transitions into discussing the extension of these concepts to functions of two variables, including the criteria for critical points and the use of the second derivative test, known as the D-test, for functions of several variables.

05:01

🔍 Applying the D-test for Multivariable Functions

The paragraph delves into the specifics of applying the D-test to functions of two variables. It explains the process of identifying critical points where both partial derivatives with respect to x and y are zero or undefined. The D-test formula is introduced, involving the second partial derivatives and the mixed partial derivative. The outcomes of the D-test are outlined, detailing the conditions under which a function has a relative maximum, minimum, or saddle point. The paragraph also discusses the inconclusive nature of the test when the second derivative at a critical point is zero, necessitating a return to the first derivative test. The explanation is supplemented with an example that demonstrates the calculation of critical points, the D-test, and the determination of a relative maximum.

10:02

📉 Saddle Points and Absolute Extrema in Multivariable Functions

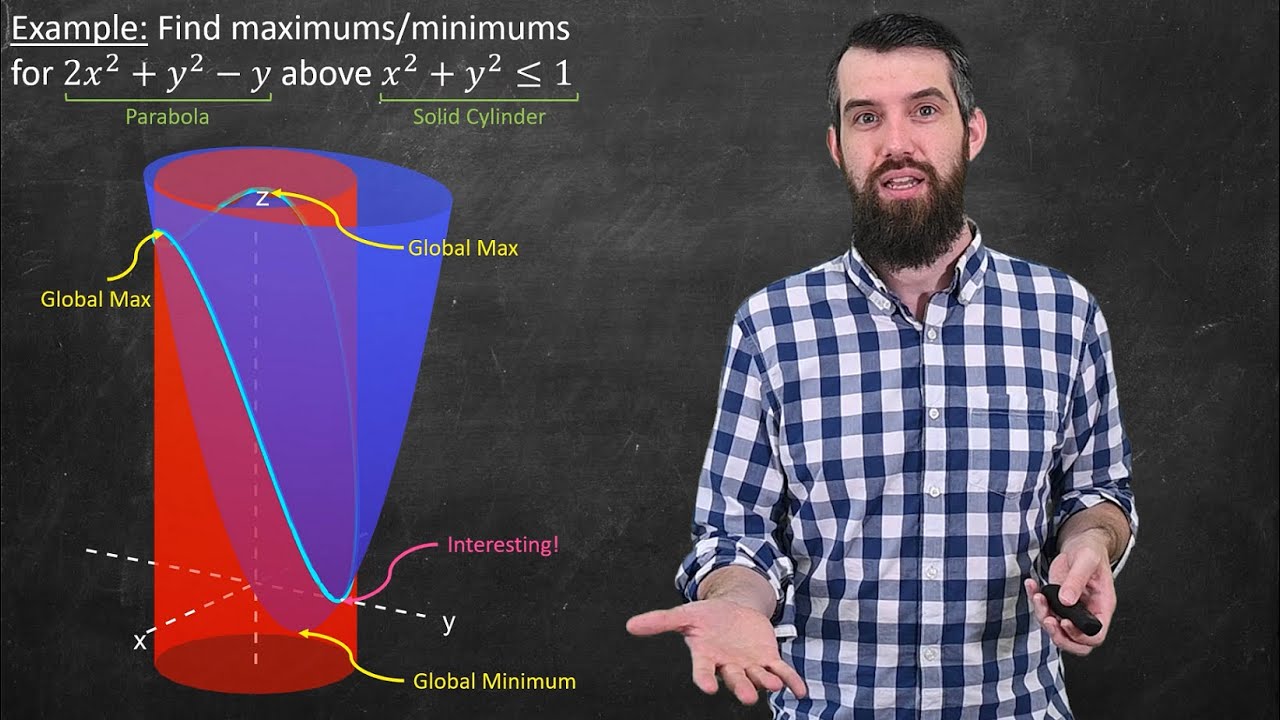
This section discusses the concept of saddle points and absolute extrema in the context of multivariable functions. It explains how to identify saddle points, which can appear as minima or maxima depending on perspective, and absolute extrema, which are the highest or lowest points on a closed interval or region. The paragraph provides a step-by-step guide on finding absolute extrema, which includes finding critical points, considering endpoints, and evaluating function values at these points. An example is given to illustrate the process, showing how to find the absolute maximum and minimum values of a function within a specified interval.

15:02

📐 Maximizing Volume with Given Constraints

The paragraph presents an application problem involving the maximization of the volume of a rectangular box with one vertex on a given plane and three faces in the coordinate planes. The problem is approached by expressing the volume as a function of two variables and using the method of Lagrange multipliers to find the dimensions that yield the maximum volume. The solution involves setting up a system of equations derived from the constraints and solving for the variables that maximize the volume function. The final step is to calculate the maximum volume using the found dimensions.

20:04

📏 Finding the Shortest Distance Between Parallel Planes

This final paragraph discusses a method for finding the shortest distance between two parallel planes using calculus. The approach involves connecting a point on one plane to an arbitrary point on the other plane and minimizing the squared distance between these points to avoid dealing with square roots. The paragraph outlines the process of setting up a function for the squared distance, taking partial derivatives with respect to the variables, and solving the resulting system of equations to find the point that minimizes the distance. The shortest distance is then obtained by taking the square root of the minimized squared distance function.

Mindmap

Keywords

💡Critical Values

Critical values are points in the domain of a function where the derivative is either zero or undefined, indicating potential maxima or minima. In the script, critical values are calculated for functions of one and several variables, serving as the foundation for finding local extrema. For instance, when discussing functions of one variable, the script mentions finding critical values by setting the first derivative equal to zero or identifying where it does not exist.

💡First Derivative Test

The first derivative test is a method used to determine whether a critical point is a relative maximum or minimum by analyzing the sign changes of the derivative around the point. The script explains that if the derivative changes from positive to negative, the function has a relative maximum at the critical point, and vice versa for a minimum. This concept is applied when discussing both single-variable and multivariable calculus.

💡Second Derivative Test

The second derivative test is used to assess the concavity of a function at a critical point to determine if it is a local extremum. If the second derivative is positive, the function is concave up, indicating a local minimum. If it is negative, the function is concave down, suggesting a local maximum. The script specifically mentions this test as a preferred method in optimization problems for functions of one variable.

💡Partial Derivatives

Partial derivatives are the derivatives of a function with respect to one variable while keeping the other variables constant. In the context of the script, partial derivatives are essential for finding critical points in functions of several variables. For example, the script describes finding critical points by setting both the partial derivative with respect to x and y to zero simultaneously.

💡Saddle Point

A saddle point is a critical point where the function neither has a local maximum nor minimum value; it is a point where the surface changes from convex to concave or vice versa. The script discusses saddle points in the context of multivariable functions, noting that if the D-test (a specific method for multivariable functions) results in a negative value, the point is a saddle point.

💡D-test

The D-test, or the second derivative test for functions of several variables, is used to determine the nature of critical points by examining the sign of a specific combination of second partial derivatives. The script introduces the D-test with the formula D = f_xx * f_yy - (f_xy)^2, and explains that the sign of D, along with the sign of f_xx, can indicate whether the function has a local maximum, minimum, or saddle point at the critical point.

💡Absolute Extrema

Absolute extrema refer to the highest and lowest values that a function attains over a specified domain. The script discusses finding absolute extrema for functions of a single variable over a closed interval and for functions of several variables over a closed region, emphasizing the need to consider boundary points and the application of the extreme value theorem.

💡Lagrange Multipliers

Although not explicitly defined in the script, Lagrange multipliers are a method hinted at for solving constrained optimization problems. This technique is used when finding extrema of a function subject to constraints, which is a natural progression from the topics discussed in the script.

💡Optimization Problems

Optimization problems involve finding maximum or minimum values of a function, often subject to certain constraints. The script connects the concepts of critical values, first and second derivative tests, and the D-test to solving optimization problems, such as finding the dimensions of a box with the largest volume or the shortest distance between parallel planes.

💡Continuous Functions

Continuous functions are those without any abrupt changes in value, which is an important property for applying the extreme value theorem. The script mentions that if a function is continuous on a closed interval or region, it guarantees the existence of absolute extrema, a key concept in understanding when and how to apply the methods for finding extrema.

💡Linear System

A linear system refers to a set of linear equations that can be solved simultaneously. In the script, the process of finding critical points for functions of several variables often involves setting partial derivatives to zero and solving the resulting linear system, as demonstrated when finding critical points for the function f(x, y) = x^2 - 3xy - y^2 + 2y - 6x.

Highlights

Introduction to the concept of maximum and minimum values for functions of several variables.

Recap of finding critical values for functions of one variable through first and second derivative tests.

Explanation of the process for identifying critical points in multivariable functions using partial derivatives.

Introduction of the D-test for functions of several variables as an analogue to the second derivative test.

Criteria for using the D-test, including the conditions for concavity and the sign of the second partial derivatives.

Application of the D-test to determine relative maxima, minima, and saddle points.

Demonstration of finding local extrema for a function of two variables with given partial derivatives.

Process of evaluating the D-test for different critical points to classify them as maxima, minima, or saddle points.

Example of a function where the second derivative test is inconclusive, necessitating the use of the first derivative test.

Discussion on absolute extrema and the conditions under which they exist for continuous functions over closed regions.

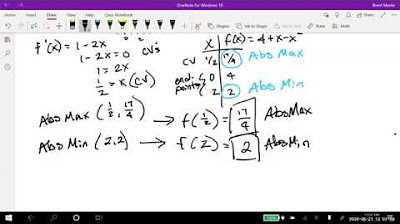
Method for finding absolute extrema of a function on a closed interval, including the use of the extreme value theorem.

Application of the process to find absolute extrema for a function defined on a specific interval.

Explanation of the process for functions of several variables to find absolute extrema over a closed region.

Example of finding absolute extrema for a function defined over a circular region.

Process for finding absolute extrema when the function is defined over a region bounded by multiple equations.

Example of identifying absolute extrema for a function on a triangular region defined by boundary equations.

Application of calculus to optimize the dimensions of a rectangular box with a given volume constraint.

Calculation of the shortest distance between two parallel planes using a multivariable function approach.

Introduction of Lagrange multipliers as a forthcoming topic for optimization problems.

Transcripts

Browse More Related Video

Multivariable Optimization with Boundaries

AP Calculus AB and BC Unit 5 Review [Analytical Applications of Differentiation]

Absolute & Local Minimum and Maximum Values - Relative Extrema, Critical Numbers / Points Calculus

Calculus 3: Lagrange Multipliers (Video #18) | Math with Professor V

Calculus Chapter 2 Lecture 14 Optimization

Math 11 - Section 3.4

Related Tags

Calculus Techniques Max Min Values Critical Points First Derivative Test Second Derivative Test D Test Optimization Problems Function Analysis Multivariable Functions Absolute Extrema