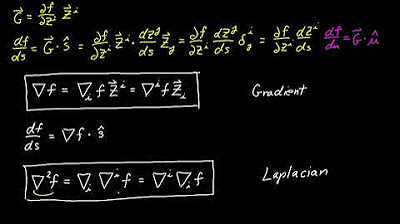Geometric Meaning of the Gradient Vector
TLDRThis video script explores the mathematical concept of gradient vectors in the context of mountain climbing. It explains how to determine the direction for the fastest ascent or to maintain a constant elevation while navigating a mountain. The script uses contour plots and the gradient vector to illustrate the principles of directional derivatives and how they relate to maximizing or minimizing changes in height. It concludes with a practical application of these concepts on a topographical map, showing how understanding contours can aid in planning routes for mountaineering.
Takeaways
- 🧗 The script discusses the mathematical concept of climbing a mountain or contouring around it by using gradient vectors.
- 📈 It introduces the idea of level curves or constant heights of a function, which are useful for visualizing changes in elevation.
- 📊 The script explains how a contour plot can be used to represent these level curves in both three-dimensional and two-dimensional forms.
- 🔍 The gradient vector is defined as a multivariable derivative that points in the direction of the steepest increase of a function.
- 📐 The tangent vector to a level curve is perpendicular to the gradient vector, indicating the direction of no change in elevation.
- 🔄 The dot product of the gradient vector and the tangent vector equals zero, indicating they are orthogonal and the function's height remains constant.
- 🏔 The script connects the mathematical concepts to real-world scenarios, such as mountain climbing and interpreting topographical maps.
- 🗺 It explains that the density of contour lines on a map can indicate steepness, with closely packed lines suggesting steep terrain.
- 🏞 The video script uses the Golden Hind mountain as an example to illustrate how to apply these concepts in a real-world context.
- ⛷ The script mentions practical applications, such as winter sports, where understanding contours can help plan routes to minimize elevation changes.
- 📚 The video aims to make calculus concepts relatable by linking them to the physical activity of mountain climbing.
Q & A
What is the purpose of a contour curve in the context of climbing a mountain?
-A contour curve represents a line of constant elevation on a mountain. It helps climbers identify the path that maintains a specific height, allowing them to contour around the mountain without gaining or losing elevation.
How can you visualize the concept of level curves or constant heights in a two-dimensional space?
-In a two-dimensional space, level curves can be visualized as the projection of three-dimensional contours onto the XY plane, showing lines that connect points of equal elevation.
What is the mathematical concept that connects the direction of steepest ascent on a mountain with calculus?
-The gradient vector is the mathematical concept that connects the direction of steepest ascent on a mountain. It is a vector that points in the direction of the greatest rate of increase of a function, which in this case is the elevation of the mountain.
Why is the dot product of the gradient vector and the tangent vector equal to zero when walking along a level curve?
-The dot product of the gradient vector and the tangent vector is zero because the gradient vector is orthogonal (perpendicular) to the level curve, indicating no change in elevation, which is the condition for walking along a level curve.
What does the directional derivative measure in the context of a mountain?
-The directional derivative measures the rate of change of the elevation function in a specific direction on the mountain. It tells you how quickly your elevation changes as you move in that direction.
What is the relationship between the gradient vector and the direction of steepest ascent on a mountain?
-The gradient vector points in the direction of the steepest ascent on a mountain. If you move in the direction of the gradient vector, you will increase your elevation the fastest.
Why are the contours close together at the base of a cliff on a topographical map?
-Contours are close together at the base of a cliff on a topographical map because small horizontal changes result in large increases in elevation, indicating a steep slope or cliff.
How can you use the concept of a gradient vector to plan a route on a topographical map?
-You can use the gradient vector to plan a route on a topographical map by identifying the direction of the steepest ascent or descent, which can help you choose a path that minimizes or maximizes elevation change based on your objective.
What does it mean for the gradient vector and a direction vector to have a 90-degree angle between them?
-When the gradient vector and a direction vector have a 90-degree angle between them, it means you are moving along a level curve with no change in elevation, as the directional derivative is at its minimum.
How can understanding the gradient vector help in mountain climbing or winter sports like skiing or snowshoeing?
-Understanding the gradient vector can help in mountain climbing or winter sports by allowing you to choose paths that contour around the mountain, minimizing the amount of uphill work required and reducing the physical exertion needed to navigate the terrain.
Outlines
📚 Mathematical Approach to Mountain Climbing
This paragraph introduces the concept of using mathematics to determine the best direction to climb a mountain or to stay at a constant elevation. It explains the use of gradient vectors in multivariable calculus to find the steepest ascent or to contour around the mountain. The script discusses the visualization of mountain elevations through contour curves and how they can be represented in both three-dimensional and two-dimensional forms. The importance of understanding the gradient vector and its relationship with the tangent vector when moving along a level curve is emphasized.
🧭 Understanding Directional Derivatives and Gradient Vectors
The second paragraph delves into the relationship between the gradient vector and the directional derivative. It explains how the dot product of the gradient vector with the tangent vector equals zero, indicating that the gradient is normal to the level curves. The concept of the directional derivative is introduced, showing how it varies with the angle between the gradient vector and a given direction vector. The paragraph illustrates that the smallest magnitude of the directional derivative occurs when moving along the level curve (tangential direction), while the largest occurs when moving in the direction of the gradient vector itself.
🏞 Real-World Application of Gradient Vectors in Topography
The final paragraph applies the mathematical concepts discussed to real-world scenarios, specifically mountain climbing and topographical maps. It describes how contour lines on a map represent constant elevation and how they can be used to plan routes that minimize or maximize elevation changes. The paragraph also touches on the practical use of understanding gradients in winter sports like skiing or snowshoeing, where contouring can reduce the effort required to navigate the terrain. The video concludes by encouraging viewers to consider the importance of these mathematical tools in outdoor activities.
Mindmap
Keywords
💡Gradient Vector
💡Contour Curve
💡Tangent Vector
💡Directional Derivative
💡Level Curves
💡Dot Product
💡Saddle Point
💡Topographical Map
💡Elevation
💡Chain Rule
Highlights
Exploring the mathematical concept of climbing a mountain by understanding the direction for ascending or contouring at a constant elevation.
Introduction to the gradient vector, a fundamental concept in multivariable calculus, and its connection to the problem at hand.
Visualizing mountain contours and their mathematical representation in both three-dimensional and two-dimensional forms.
The utility of contour plots in visualizing and understanding changes in elevation without altering height.
Derivation of the relationship between the gradient vector and the tangent vector of a level curve using calculus.
Interpretation of the dot product in the context of the gradient vector and the tangent vector to a level curve.
Understanding that the gradient vector is normal to the level curve, providing insight into the direction of no height change.
Explaining the concept of directional derivatives and their relevance to the steepness of a slope on a mountain.
Relating the directional derivative to the dot product of the gradient vector and a direction vector.
Identifying the minimal slope occurs when moving along the level curve (tangent vector), and the maximal slope when moving in the direction of the gradient vector.
Applying calculus to real-world scenarios, such as mountain climbing and understanding the practical implications of gradient vectors.
Using topographical maps to navigate mountains by analyzing contours and planning routes to minimize uphill effort.
The importance of understanding the gradient vector for activities like skiing or snowshoeing to avoid excessive elevation changes.
Practical advice on contouring in mountain climbing to reduce the amount of uphill work required.
Combining mathematical concepts with real-world mountain climbing to provide a unique perspective on calculus applications.
Encouraging viewers to like the video and leave comments for further exploration of mathematical concepts in future videos.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: