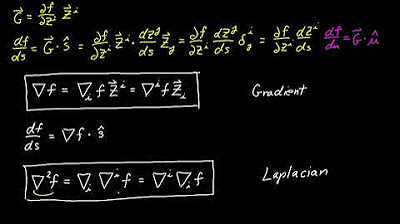Directional Derivatives | What's the slope in any direction?
TLDRThis video delves into directional derivatives, a concept in multivariable calculus that measures the rate of change of a function in any given direction. The instructor explains the traditional partial derivatives with respect to X and Y, then introduces the directional derivative as the slope in an arbitrary direction. Using a unit vector to represent direction, the video demonstrates how to compute the directional derivative through the gradient of a function, simplifying the process with the dot product of the gradient and the direction vector. An example illustrates the concept, showing how to find the slope of a function at a specific point in a chosen direction, highlighting the practicality and elegance of this mathematical tool.
Takeaways
- 📈 Directional derivatives measure the slope in any direction, unlike partial derivatives which measure slope parallel to x or y axes.
- 🧮 For partial derivatives, x or y is fixed while the other variable changes, simplifying the surface into a one-dimensional curve.
- 🔄 Directional derivatives allow us to find the slope in any chosen direction, represented by a unit vector.
- 💡 The definition of a directional derivative involves a limit of difference quotients, similar to single-variable calculus.
- 🔗 Directional derivatives can be computed using a composition of functions and applying the chain rule.
- 🧮 The formula for the directional derivative combines the partial derivatives of the function and the components of the direction vector.
- 🧭 The gradient vector, composed of the partial derivatives, simplifies the computation of directional derivatives through a dot product with the direction vector.
- 🔢 Directional derivatives in the x and y directions can be extended to any other direction using the dot product of the gradient and the direction vector.
- 📊 An example function, 2 - x^2 - y^2, illustrates the process of computing directional derivatives using the gradient and direction vector.
- 🔄 The computation shows that the directional derivative in a specific normalized direction results in a slope of zero, indicating a horizontal tangent line at that point.
Q & A
What is the main topic of the video?
-The main topic of the video is directional derivatives in multivariable calculus, which describe the slope of a function in any particular direction.
What are the differences between partial derivatives with respect to X and Y?
-Partial derivatives with respect to X and Y are used to find the slope of a function in the direction parallel to the X or Y axis, respectively. When taking the partial derivative with respect to X, Y is considered fixed, and vice versa.
What is the geometric interpretation of a partial derivative?
-Geometrically, a partial derivative represents the slope of a function along a path that is parallel to the X or Y axis, depending on which variable is being differentiated with respect to.
What is a directional derivative?
-A directional derivative is the rate of change of a function in a specified direction, not necessarily parallel to the coordinate axes.
How is the direction of the derivative related to the direction vector?
-The direction of the derivative is determined by a unit vector, which indicates the direction in which the slope of the function is being measured.
What is the definition of the directional derivative mathematically?
-The directional derivative is defined as the limit of the difference quotient of the function values at two points, as the points approach each other along the direction vector.
How can we compute the directional derivative using the gradient?
-The directional derivative can be computed as the dot product of the gradient of the function and the direction vector.
What is the gradient of a function?
-The gradient of a function is a vector whose components are the partial derivatives of the function with respect to each variable.
Can you provide an example of calculating a directional derivative?
-Sure, for the function f(x, y) = 2 - x^2 - y^2 at the point (1/2, -1/2) in the direction vector (1/√2, 1/√2), the directional derivative is calculated by taking the dot product of the gradient at that point with the direction vector, which results in 0.
What does a zero directional derivative indicate geometrically?
-A zero directional derivative indicates a horizontal tangent line to the function's graph at that point, suggesting no change in the function's value in the direction of the derivative.
How does the video suggest visualizing the concept of directional derivatives?
-The video suggests visualizing directional derivatives by considering the secant line between two points on the function's graph along the direction vector and taking the limit as these points approach each other.
Outlines
📚 Introduction to Directional Derivatives
This paragraph introduces the concept of directional derivatives, which are used to determine the slope of a function in any given direction. It contrasts these with partial derivatives, which only consider changes in one variable at a time. The paragraph explains how partial derivatives are used to find the slope along paths parallel to the X or Y axes, while directional derivatives generalize this to any direction. It also sets up the mathematical framework for calculating directional derivatives by considering a unit vector in a particular direction and parameterizing points along that direction from a given point in the function's domain.
🔍 Calculating Directional Derivatives Using the Gradient
The second paragraph delves into the computation of directional derivatives. It explains how to use the gradient of a function, a vector of partial derivatives, to find the directional derivative in any direction. The paragraph illustrates the process by considering the derivative of a composition of functions and applying the chain rule. It simplifies the computation to a dot product between the gradient and the direction vector, highlighting the ease and generality of this method. The paragraph also introduces the notation for the gradient and emphasizes the usefulness of this approach in calculating directional derivatives efficiently.
📈 Example Calculation of Directional Derivatives
In this paragraph, an example is provided to demonstrate the calculation of directional derivatives. The function given is f(x, y) = 2 - x^2 - y^2, and the calculation is performed at the point (1/2, -1/2) in the direction of the vector (1/√2, 1/√2). The paragraph shows how to compute the partial derivatives of the function, evaluate them at the given point, and then use these to find the directional derivative by taking the dot product with the direction vector. The result of this calculation is zero, indicating a horizontal tangent plane at the specified point, which is visualized and explained in the context of the function's geometry.
Mindmap
Keywords
💡Directional Derivatives
💡Partial Derivatives
💡Unit Vector
💡Slope
💡Multivariable Calculus
💡Derivative
💡Secant Line
💡Chain Rule
💡Gradient
💡Dot Product
💡Tangent Line
Highlights
Introduction to directional derivatives and their role in determining the slope in any specific direction.
Explanation of partial derivatives with respect to X and Y and how they relate to the slope of a curve in a fixed direction.
The geometric interpretation of partial derivatives as the slope in the direction parallel to the X or Y axis.
The concept of extending the idea of partial derivatives to any arbitrary direction using a unit vector.
Parametrization of points in the direction of a unit vector to define the directional derivative.
Definition of the directional derivative through a limit of difference quotients.
Visual representation of the directional derivative as the slope of a secant line between two points on the function's graph.
Derivation of the formula for the directional derivative using the chain rule and composition of functions.
Introduction of the gradient vector as a shorthand for the partial derivatives of a function.
Expression of the directional derivative as a dot product between the gradient and the direction vector.
Practical computation of the directional derivative using partial derivatives and the dot product.
Example calculation of the directional derivative for a given function and point in a specific direction.
Visualization of the directional derivative as a horizontal tangent line at a critical point.
Discussion on the ease of computing directional derivatives once partial derivatives are known.
Invitation for viewers to leave questions in the comments for further discussion on the topic.
Encouragement for viewers to like the video and support the channel for more educational content.
Promotion of a larger playlist on multivariable calculus for those interested in further learning.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: