Types of Experimental Research Designs - CRD RBD RCBD LSD FD - Research Methods - Practical Research
TLDRThis script delves into four primary experimental research designs: Completely Randomized Design (CRD), Randomized Block Design (RBD), Latin Square Design (LSD), and Factorial Design (FD). It explains the conditions for using each design, the process of assigning treatments, and the calculation of required experimental units. The script also highlights the advantages and limitations of each design, such as CRD's simplicity and RBD's control over heterogeneity, LSD's control over more variables, and FD's ability to examine multiple factors and interactions, providing a comprehensive guide for researchers in designing effective experiments.
Takeaways
- 🔬 There are four main types of experimental research designs: Completely Randomized Design (CRD), Randomized Block Design (RBD), Latin Square Design (LSD), and Factorial Design (FD).
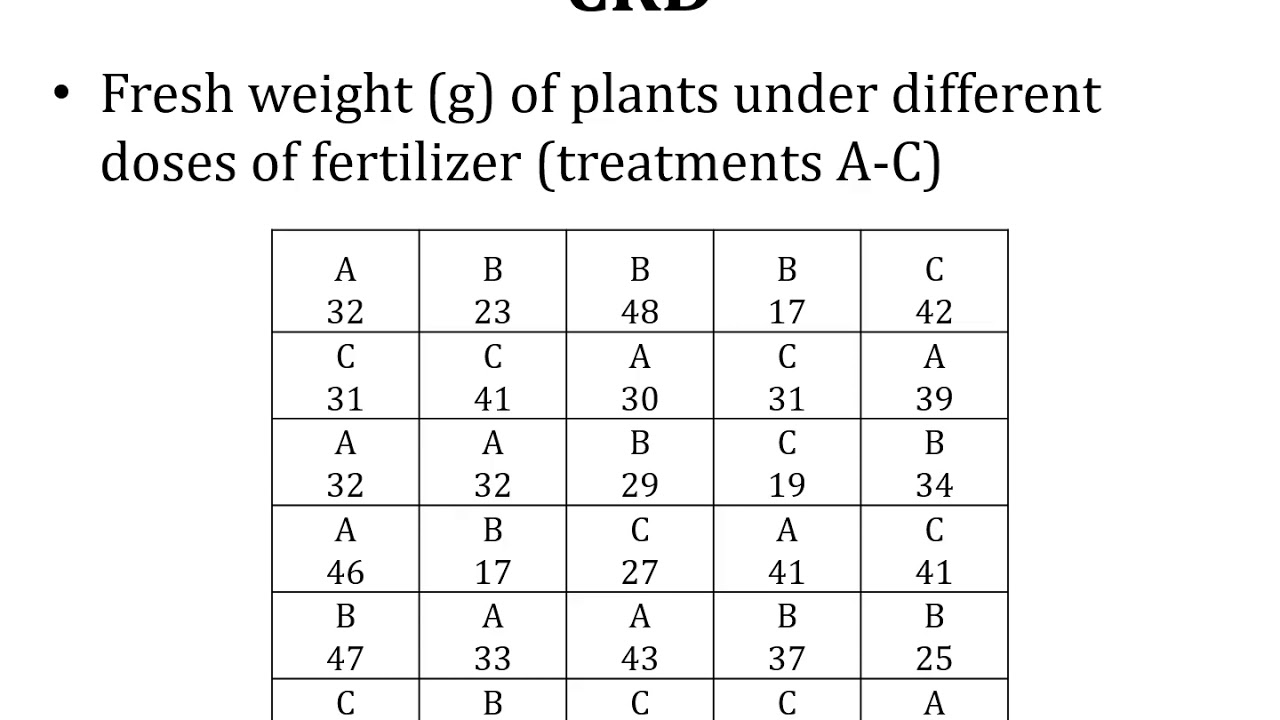
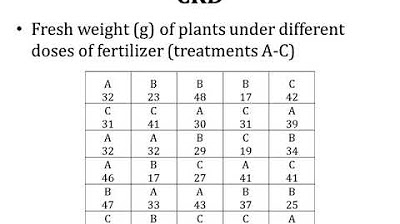
- 🎯 CRD is used when experimental units form a homogeneous group, such as day-old chicks of the same breed or young laboratory animals.
- 📐 In CRD, the total number of experimental units required is determined by error degrees of freedom, with a minimum of 10 for precise significance testing.
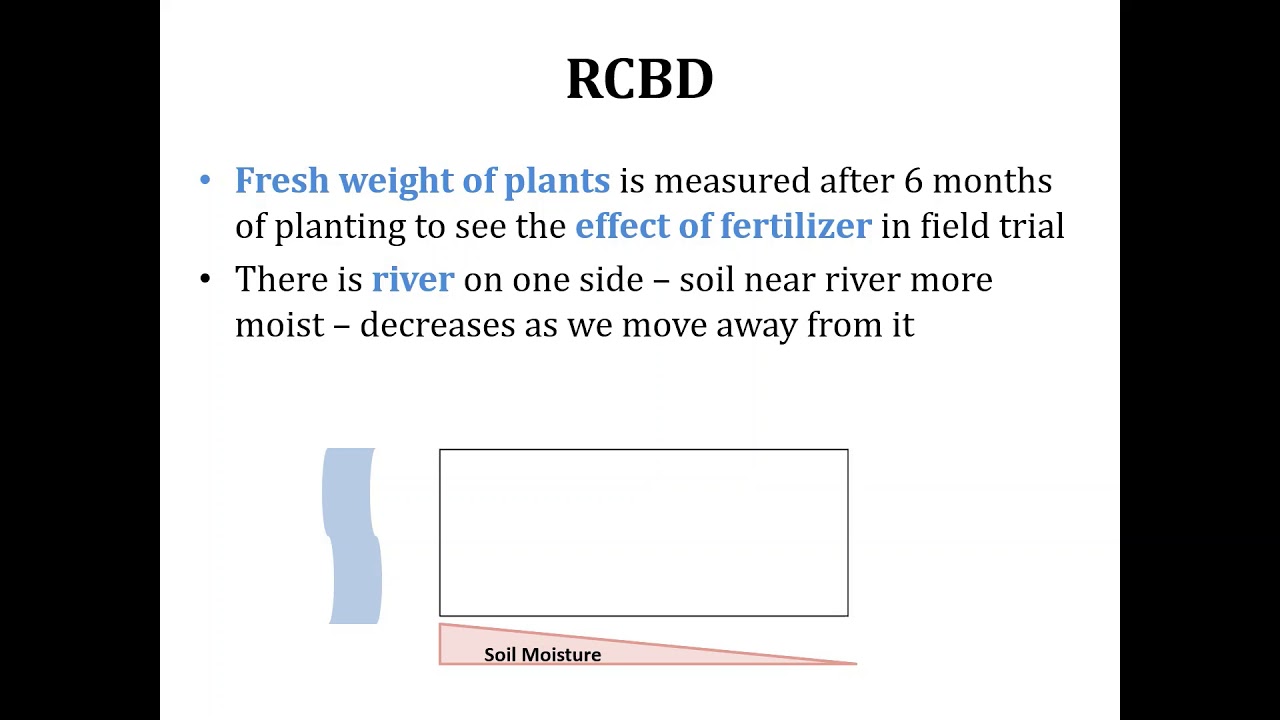
- 🧩 RBD is an improvement over CRD, applied when experimental units are heterogeneous, grouping them into homogeneous blocks to reduce variability.
- 📊 The error degrees of freedom in RBD should also be at least 10, and the design allows for the control of one source of variation through blocking.
- 🌟 LSD is used when the number of treatments equals the number of replications, with treatments arranged in a square to control more variation than CRD or RBD.
- 🌱 An example of LSD includes an agricultural experiment with seed variety and soil fertility factors, where treatments are randomly allocated to rows and columns.
- 🔍 FD allows for the examination of main effects of multiple independent variables and the detection of interactions among them.
- 🔄 FD can include various combinations of factors, such as a two by two, three by three, or a more complex factorial design involving multiple factors.
- 📝 The script provides detailed examples and formulas for calculating the number of experimental units needed for each design, emphasizing the importance of error degrees of freedom.
- 📉 One of the limitations of LSD is the assumption of no interaction between factors, which may not hold true in all cases, and its application is best suited for a smaller number of treatments (5-10).
- 🚫 The complexity of statistical analysis in LSD increases with missing data, but unlike RBD, it allows for easier omission of data without complicating the analysis.
Q & A
What are the four main types of experimental research designs mentioned in the script?
-The four main types of experimental research designs mentioned are Completely Randomized Design (CRD), Randomized Block Design (RBD), Latin Square Design (LSD), and Factorial Design (FD).
Under what conditions is the Completely Randomized Design (CRD) used?
-CRD is used when experimental units form a homogeneous group, such as day-old chicks of the same breed, young laboratory animals, or plots of land in the same field, and when the allotment of treatment to the experimental units is completely random.
What is the minimum error degrees of freedom required for a precise test of significance in CRD?
-For a precise test of significance in CRD, the minimum error degrees of freedom should be at least 10.
How is the total number of experimental units required in a CRD experiment determined?
-In CRD, the total number of experimental units required is decided by error degrees of freedom and can be calculated using the formula n = T * (n - 1) / error DF, where T is the number of treatments.
What is the advantage of using Randomized Block Design (RBD) over CRD?
-RBD is an improvement over CRD as it is applied when experimental units are heterogeneous. It groups experimental units into homogeneous blocks according to variability, which helps in controlling more variation and making treatment comparisons more efficient.
How does the number of blocks in RBD relate to the number of treatments and error degrees of freedom?
-In RBD, the number of blocks can be computed using the formula (B - 1) * (T - 1) = error DF, where B is the number of blocks and T is the number of treatments.
What is the main characteristic of Latin Square Design (LSD) that distinguishes it from other designs?
-The main characteristic of LSD is that the number of treatments is equal to the number of replications, and treatments are allocated in such a way that every treatment occurs once and only once in each row and column.
What are the advantages of using Latin Square Design (LSD)?
-LSD controls more variation than CRD or RBD, has simple statistical analysis, can handle missing data relatively simply, and allows for the investigation of more than one factor simultaneously with fewer trials.
What is the main purpose of Factorial Design (FD) in experimental research?
-The main purpose of FD is to allow researchers to examine the main effects of two or more individual independent variables simultaneously and to detect interactions among variables.
What is an interaction in the context of Factorial Design?
-An interaction in Factorial Design is when the effects of one variable vary according to the levels of another variable, which can only be detected when the variables are examined in combination.
What are some examples of independent variables that could be studied in a Factorial Design?
-Examples of independent variables in a Factorial Design could include different levels of treatments, settings, dosages, seed varieties, or soil fertility levels.
Outlines
🔬 Fundamentals of Experimental Research Designs
This paragraph introduces the concept of experimental research designs, focusing on four main types: Completely Randomized Design (CRD), Randomized Block Design (RBD), Latin Square Design (LSD), and Factorial Design (FD). It explains that CRD is suitable for homogeneous groups, such as day-old chicks of the same breed or similar agricultural plots. The paragraph details the random allocation of treatments in CRD and provides a formula for calculating the number of experimental units required, emphasizing the need for a minimum of 10 error degrees of freedom for statistical significance. An example calculation for an experiment with five treatments is given, illustrating the process of determining the number of replications and total units needed.
🌱 Enhancing Experiments with Randomized Block Design
The second paragraph delves into the Randomized Block Design, an improvement over CRD for heterogeneous experimental units. It discusses how units are grouped into homogeneous blocks based on variability, with the number of units in each block being a multiple of treatments. Examples include different animal breeds, agricultural plots in various fields, or plants under different environmental conditions. The paragraph outlines the random allocation of treatments within blocks and provides a formula for calculating the error degrees of freedom and the total number of experimental units. It also mentions the advantages of RBD, such as simplicity in design and statistical analysis, and its limitations when dealing with a large number of treatments or missing data.
🎛️ Controlling Variation with Latin Square Design
The Latin Square Design is introduced in this paragraph as an experimental design where the number of treatments equals the number of replications. It describes the arrangement of experimental units in a square format and the random allocation of treatments to rows and columns, ensuring each treatment appears once per row and column. The paragraph provides examples of an experiment with three treatments and an agricultural experiment involving seed variety and soil fertility. It highlights the advantages of LSD, such as controlling more variation than CRD or RBD and allowing for simple statistical analysis even with missing data. However, it also notes the limitations, including the assumption of no interaction between factors and suitability for a limited number of treatments.
📊 Exploring Interactions with Factorial Design
The final paragraph discusses the Factorial Design, which allows researchers to manipulate multiple independent variables and examine their main effects and interactions. It explains that interactions occur when the effect of one variable changes with the levels of another. The paragraph provides examples of factorial designs with different levels of independent variables, such as a two-by-two, two-by-three, three-by-four, and a complex two-by-two-by-three design. It emphasizes the benefits of factorial designs in studying the effects of multiple variables simultaneously and detecting interactions that cannot be identified when variables are examined in isolation.
Mindmap
Keywords
💡Experimental Research Design
💡Completely Randomized Design (CRD)
💡Randomized Block Design (RBD)
💡Latin Square Design (LSD)
💡Factorial Design (FD)
💡Homogeneous Group
💡Error Degrees of Freedom
💡Replications
💡Treatments
💡Interactions
💡Independent Variables
Highlights
There are four main types of experimental research designs: Completely Randomized Design (CRD), Randomized Block Design (RBD), Latin Square Design (LSD), and Factorial Design (FD).
CRD is used when experimental units form a homogeneous group, such as day-old chicks of the same breed or young laboratory animals.
In CRD, treatments are allotted to experimental units completely at random, with the total number of units decided by error degrees of freedom.
For precise test of significance in CRD, the minimum error degrees of freedom should be at least 10.
An example calculation for CRD is provided, illustrating the number of experimental units required for five treatments with 10 error degrees of freedom.
CRD is easy to design and analyze, but requires a homogeneous set of experimental units for efficient treatment comparison.
RBD is an improvement over CRD, applied when experimental units are heterogeneous and grouped into homogeneous blocks.
RBD uses local control or blocking to eliminate assignable causes of variation among experimental units.
The error degrees of freedom in RBD is lesser than CRD due to the removal of degrees of freedom per block.
LSD is suitable when the number of treatments equals the number of replications, with treatments allocated to rows and columns to control more variation.
LSD allows for the investigation of more than one factor simultaneously with fewer trials than more complicated designs.
Factorial Design manipulates multiple independent variables to examine main effects and interactions among variables.
Factorial Design can have various configurations, such as two by two, two by three, three by four, and so on.
An example of a two by two by three factorial design is given, involving treatment, setting, and dosage as independent variables.
The advantages of different experimental designs are discussed, including simplicity, control of variation, and the ability to detect interactions.
The limitations of each design, such as the need for homogeneous units in CRD and the complexity with missing data in RBD, are also highlighted.
The importance of error degrees of freedom in determining the number of experimental units required for each design is emphasized.
The transcript provides detailed examples and illustrations for each experimental design, aiding in understanding and application.
Transcripts
Browse More Related Video
Experimental Designs; Randomized Complete Block Design; RCBD; Two-Way ANOVA
Experimental Designs; CRD; Completely Randomized Design; One-Way ANOVA
Types of Experimental Designs (3.3)
Lecture 18 Experimental Designs; Completely Randomized Design CRD; One Way ANOVA

Analyse data from experiments with completely randomised design (CRD)

QUANTITATIVE Research Design: Everything You Need To Know (With Examples)
5.0 / 5 (0 votes)
Thanks for rating: