Experimental Designs; CRD; Completely Randomized Design; One-Way ANOVA
TLDRThe video explains the Completely Randomized Design (CRD), a basic experimental design where treatments are assigned randomly to experimental units. It highlights CRD's application in homogeneous conditions like lab experiments to minimize experimental error. The speaker details an example involving fertilizer doses on plant growth, demonstrating the statistical analysis process through one-way ANOVA. The results indicate no significant effect of fertilizer doses on the fresh weight of plants, emphasizing the importance of controlled conditions and replication in reducing variability.
Takeaways
- 🔬 The script discusses the Completely Randomized Design (CRD), a fundamental experimental design used in field research where treatments are assigned at random to experimental units.
- 🧪 CRD is suitable for homogeneous experimental units, such as lab experiments, where environmental conditions can be easily controlled to minimize experimental error.
- 📝 The purpose of an experiment is to observe the differences in the response of experimental units to various treatments, with treatments being categories of the independent variable.
- 🌱 In CRD, each experimental unit has an equal chance of receiving any of the treatments, ensuring that the assignment is unbiased.
- ⚖️ The script emphasizes the importance of replication in CRD, ensuring that there are enough replicates of each treatment to validate the results.
- 📊 The experimental error in CRD arises from extraneous factors beyond the control of the experimenter, which is why CRD is best suited for controlled environments.
- 📚 The script explains that CRD is simple and basic but effective under homogenous environmental conditions, typically found in lab settings.
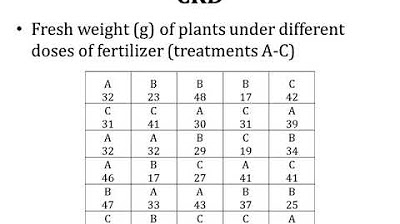
- 📈 The example provided in the script illustrates how CRD is applied in an experiment to determine the effects of different fertilizer doses on the fresh weight of plants.
- 📊 The statistical analysis of CRD data is typically performed using one-way ANOVA, which compares the means of different treatment groups.
- 📉 The example's one-way ANOVA result indicated that there was no significant effect of different fertilizer doses on the fresh weight of plants, suggesting that the treatments did not influence the response variable as expected.
- 📝 The script concludes by summarizing the process of CRD, from treatment assignment to statistical analysis, highlighting its application in controlled experimental conditions.
Q & A
What is the Completely Randomized Design (CRD)?
-The Completely Randomized Design (CRD) is an experimental design where treatments are assigned completely at random to the experimental units. It is one of the three types of experimental designs used in field research, along with Randomized Complete Block Design (RCBD) and Latin Square Design.
What are treatments in the context of CRD?
-In CRD, treatments refer to the categories of the independent variable that are applied to the experimental units to observe the response of the dependent variable.
How are treatments assigned in CRD?
-In CRD, treatments are assigned completely at random to the experimental units, ensuring that each experimental unit has the same chance of receiving any of the treatments.
What is the purpose of assigning treatments randomly in CRD?
-Assigning treatments randomly in CRD helps to control for extraneous factors and reduce experimental error, allowing researchers to more accurately attribute differences in the response variable to the treatments themselves.
Under what conditions is CRD considered appropriate?
-CRD is appropriate for situations where experimental units are homogeneous and environmental conditions can be easily controlled, such as in laboratory experiments.
What is the concept of replication in experimental design?
-Replication in experimental design refers to the practice of applying the same treatment to different experimental units to ensure that the results are consistent and reliable.
What is the role of randomization in CRD?
-Randomization in CRD ensures that treatments are applied to experimental units in a way that minimizes bias, allowing for more valid comparisons between the effects of different treatments.
What are the two main sources of variation in CRD?
-The two main sources of variation in CRD are the treatments (the intentional variation of interest) and experimental error (unintended variation due to extraneous factors).
How is the data from a CRD experiment typically analyzed?
-The data from a CRD experiment is typically analyzed using one-way ANOVA (Analysis of Variance) to determine if there are significant differences between the means of the treatments.
What does a non-significant result in a one-way ANOVA indicate?
-A non-significant result in a one-way ANOVA indicates that there is not enough evidence to conclude that the treatments have a significant effect on the response variable, suggesting that the differences observed may be due to experimental error rather than the treatments themselves.
Can you provide an example of how CRD is applied in a real-world scenario?
-An example of CRD application is in an experiment to determine the effects of different fertilizer doses on the fresh weight of plants. In this scenario, plants are the experimental units, fertilizer doses are the treatments, and the fresh weight of plants is the response variable measured to assess the impact of the treatments.
Outlines
🔬 Introduction to Completely Randomized Design (CRD)
The first paragraph introduces the concept of the Completely Randomized Design (CRD), which is a fundamental type of experimental design used in field research. It explains that treatments, representing categories of the independent variable, are assigned randomly to experimental units to observe the response of the dependent variable. The purpose of the experiment is to identify differences in responses to various treatments, with any variation among units receiving the same treatment attributed to experimental error. CRD is suitable for homogeneous experimental units where environmental conditions are easily controlled, such as in laboratory settings. The paragraph also emphasizes the importance of replication and randomization in CRD to reduce error and ensure the validity of experimental results.
🌱 Randomization and Sources of Variation in CRD
This paragraph delves into the process of randomization in CRD, illustrating how treatments are applied without any specific pattern to experimental units kept under similar conditions to minimize experimental error. It identifies the two main sources of variation in CRD: treatments, which are the intended source of variation, and experimental error, which arises from uncontrollable extraneous factors. The paragraph explains the goal of experimental design to reduce experimental error and highlights the simplicity of CRD, making it suitable for environments with controlled conditions. An example is provided to demonstrate the application of CRD in an experiment studying the effects of fertilizer doses on plant growth.
📊 Data Analysis Using One-Way ANOVA in CRD
The third paragraph discusses the statistical analysis of data obtained from a CRD experiment, specifically using one-way ANOVA. The process begins with organizing data according to treatments and calculating descriptive statistics, including mean values and variances. The homogeneity of variances is tested using the F max test, ensuring that variances among treatments are not significantly different. The paragraph outlines the steps for calculating the correction term, total sum of squares, treatment sum of squares, and sum of squares for experimental error, which are essential for conducting the ANOVA.
📐 Calculation of ANOVA Components and Degrees of Freedom
This paragraph continues the explanation of the ANOVA process by detailing the calculation of the correction term, total sum of squares, treatment sum of squares, and sum of squares for experimental error. It describes how to verify these calculations and move on to determining degrees of freedom for total, treatment, and error. The paragraph also explains the calculation of mean squares (MS) for treatments and experimental error, which are crucial for the F test to compare variances.
📉 Conclusion of ANOVA and Implications for CRD
The final paragraph concludes the ANOVA process by comparing the variances through the F test. It calculates the F value and compares it with the critical F value to determine the significance of the results. In this case, the result is non-significant, indicating that the different fertilizer doses did not affect the fresh weight of plants. The paragraph summarizes the findings in an ANOVA summary table and states the conclusion that there is no effect of fertilizer dose on plant growth under the CRD setup. It reinforces the understanding of CRD and its application in controlled experimental conditions.
Mindmap
Keywords
💡CRD (Completely Randomized Design)
💡Experimental Design
💡Treatments
💡Experimental Units
💡Dependent Variable
💡Replication
💡Randomization
💡Homogeneous Environmental Conditions
💡Experimental Error
💡One-Way ANOVA
💡Significance
Highlights
CRD (Completely Randomized Design) is the first type of experimental design discussed, suitable for situations where treatments are assigned at random to experimental units.
CRD assumes that experimental units have the same chance of receiving any treatment, minimizing the impact of extraneous factors.
The purpose of an experiment is to observe differences in the response of experimental units to various treatments.
Experimental error arises from uncontrolled extraneous factors, which should be minimized in a well-designed experiment.
CRD is appropriate for homogeneous experimental units and controlled environments, such as lab experiments.
Replication is a key principle of CRD, ensuring multiple experimental units receive the same treatment for reliable results.
Randomization in CRD is crucial for reducing experimental error by assuming all units are under similar conditions.
Sources of variation in CRD are limited to treatments and experimental error, simplifying the analysis.
The total variability in CRD is the sum of variability due to treatments and experimental error.
CRD's simplicity makes it a basic yet effective experimental design for controlled environments.
An example of CRD application is studying the effects of fertilizer dose on the fresh weight of plants.
In the example, one-way ANOVA is used to analyze the impact of different fertilizer doses on plant growth.
Descriptive statistics, such as mean values and variances, are essential for the ANOVA computation.
The F max test is used to check the homogeneity of variances between treatments in CRD.
The correction term for ANOVA is calculated to adjust the total sum of squares.
The ANOVA summary table organizes the results, including sources of variation, sum of squares, degrees of freedom, and F values.
The final result of the example shows no significant effect of fertilizer dose on plant fresh weight, indicating the importance of proper experimental design interpretation.
Transcripts
Browse More Related Video
Lecture 18 Experimental Designs; Completely Randomized Design CRD; One Way ANOVA
Experimental Designs; Randomized Complete Block Design; RCBD; Two-Way ANOVA

Types of Experimental Research Designs - CRD RBD RCBD LSD FD - Research Methods - Practical Research

Analyse data from experiments with completely randomised design (CRD)
Types of Experimental Designs (3.3)

Introduction to Experimental Designs; Principles; Randomization; Replication; Local Control
5.0 / 5 (0 votes)
Thanks for rating: