2^k Factorial Designs Experiment - ANOVA Model
TLDRThis lecture delves into factorial designs, a pivotal topic in hypothesis testing within probability and statistics. Dr. Gurk, from the School of Mathematics, extends the discussion on two-factor experiments to explore designs with multiple factors, such as 2^k factorial designs. The lecture explains how to analyze the impact of factors and their interactions on experiments using geometric notation and introduces the concept of main effects and interaction factors. It also covers the construction of ANOVA tables and the calculation of sum of squares, mean sum of squares, and F-ratios to test hypotheses, providing methods to determine significant effects in experimental designs.
Takeaways
- 📚 The lecture introduces factorial design, a significant topic in hypothesis testing within the realm of probability and statistics.
- 🔍 The script explains the concept of a two-factor factorial experiment, which is an extension of the basic factorial experiment discussed in a previous lecture.
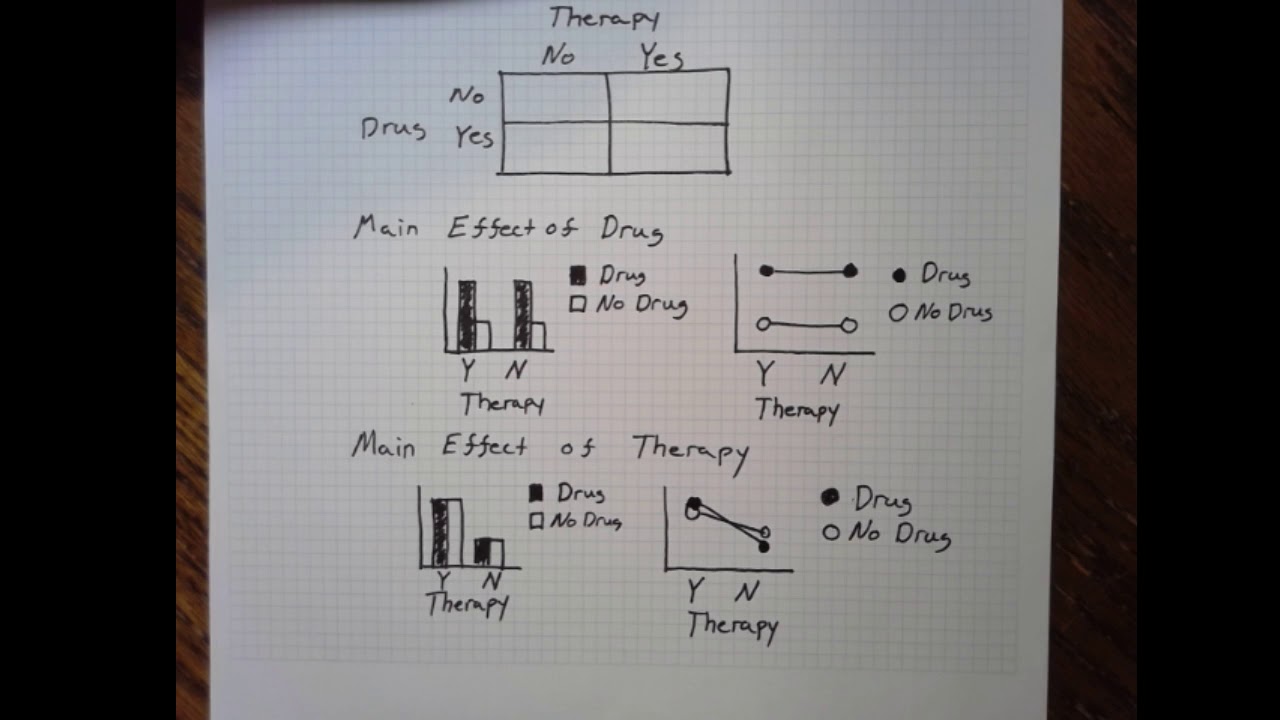
- 🔢 The factorial design is denoted as 2^k, where 'k' represents the number of factors, each with two levels (e.g., high and low), leading to 2^k possible combinations.
- 📝 The script uses geometric notation (+ and -) to represent the high and low levels of factors, which is a standard method in factorial design.
- 📈 The lecture covers how to construct an ANOVA (Analysis of Variance) table, which is essential for analyzing the impact of different factors and their interactions on experimental outcomes.
- 🔧 The script explains two methods for calculating the sum of squares for factors and interactions: the direct method and the more efficient z-method.
- 📉 The importance of calculating degrees of freedom is highlighted, which is crucial for determining the significance of factors and interactions in the experiment.
- 📊 The process of finding the main effects and interaction effects of factors is detailed, including how to interpret these effects in the context of the experiment.
- 📚 The script provides examples of 2^k factorial designs, illustrating how to apply the concepts discussed to real-world experimental scenarios.
- 📉 The method for calculating F-ratios and comparing them with critical values to determine the significance of the factors is explained.
- 🔑 The lecture emphasizes the importance of understanding factorial designs for hypothesis testing and the analysis of experimental data.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is factorial design, specifically 2k factorial experiments in the context of hypothesis testing.
What is a 2k factorial design?
-A 2k factorial design is an experimental design with k factors, each at two levels (e.g., high and low), resulting in 2^k possible combinations of these levels.
What are the two levels in a factorial experiment typically referred to as?
-The two levels in a factorial experiment are typically referred to as 'high' and 'low', or in geometric notation, as 'positive' and 'negative'.
What does the term 'geometric notation' in factorial design refer to?
-Geometric notation in factorial design refers to the use of plus and minus signs to represent the high and low levels of the factors, respectively.
What is the purpose of the factorial design in experimental analysis?
-The purpose of factorial design in experimental analysis is to study the effects of multiple factors and their interactions on the outcome of an experiment.
What is the significance of the equal number of positive and negative signs in each column of a factorial design table?
-The equal number of positive and negative signs in each column ensures that each factor is tested equally at both levels, which helps in unbiased analysis of the experimental results.
How are the interactions between factors represented in a factorial design?
-The interactions between factors in a factorial design are represented by the product of the factors involved, such as AB, AC, or BC, where capital letters denote the factors and lowercase letters represent their combinations.
What is the method for finding the sum of squares (SS) for the factors and interactions in an ANOVA table?
-The sum of squares for the factors and interactions in an ANOVA table can be found using the contrast values, which are calculated based on the levels of the factors and their combinations.
What is the Z-method mentioned in the script, and how does it simplify the calculation process in factorial designs?
-The Z-method is an alternative approach to calculating the sum of squares and other values in a factorial design. It simplifies the process by using the totals of the factor levels and their combinations, reducing the complexity of calculations, especially for larger designs.
How can you determine if a factor or interaction is significant in a factorial experiment?
-A factor or interaction is determined to be significant if the calculated F-ratio for that effect is greater than the critical value from the F-distribution table at a given level of significance.
What are the three examples provided in the script, and what do they demonstrate?
-The three examples provided in the script demonstrate the application of factorial design in different scenarios: (1) A basic 2^2 factorial design with two factors at two levels, (2) A 2^2 factorial design with additional considerations for levels as qualitative or quantitative, and (3) A 2^3 factorial design, introducing the concept of blocks in the experiment.
Outlines
📚 Introduction to Factorial Design
This paragraph introduces the concept of factorial design in the context of hypothesis testing, specifically focusing on the 2k factorial design. Dr. Gurk, from the School of Mathematics, emphasizes the importance of understanding two-factor factorial experiments before delving into more complex designs. The explanation covers the basics of factorial design, including the significance of factors, levels, and the notation used to represent them. The concept of geometric notation and the importance of maintaining an equal number of positive and negative levels for each factor are highlighted.
🔍 Detailed Explanation of 2k Factorial Designs
The second paragraph delves deeper into the 2k factorial design, explaining the methodology for analyzing the impact of multiple factors on experimental outcomes. It discusses the process of calculating degrees of freedom, sum of squares, and the construction of ANOVA tables. The paragraph also introduces the z-method for simplifying calculations in factorial designs, particularly for larger k values, and explains how to calculate main effects and interaction effects using this method.
📈 Calculation Techniques in Factorial Designs
This paragraph focuses on the calculation techniques used in factorial designs, particularly for 2^k factorial designs. It explains the process of finding the sum of squares for factors and interactions, and how to use these values to construct ANOVA tables. The paragraph also discusses two methods for calculating these sums: a direct method and a more efficient z-method, which simplifies calculations by using the addition and subtraction of treatment totals. The importance of understanding the grand total, degrees of freedom, and the significance of f-ratios in hypothesis testing is also highlighted.
📝 Examples of 2^2 Factorial Designs
The fourth paragraph provides examples of how to apply the concepts discussed in the previous paragraphs to solve 2^2 factorial design problems. It outlines the steps for setting up the problem, calculating the necessary sums of squares, and filling out the ANOVA table. The paragraph also demonstrates how to interpret the results, including determining the significance of main effects and interactions between factors.
🔢 Advanced Calculations in Factorial Designs
This paragraph extends the discussion to more complex factorial designs, specifically 2^3 factorial designs, and introduces the concept of block experiments. It explains how to adjust calculations for block designs and provides a detailed example of how to calculate sums of squares for blocks, factors, and interactions. The paragraph also emphasizes the importance of simplifying calculations by subtracting a common value from observations to ease the computation process.
📉 Evaluating Factorial Design Experiments
The sixth paragraph concludes the script by summarizing the process of solving 2^2 factorial design experiments and hints at the next class, where 2^3 factorial design problems will be discussed. It emphasizes the importance of understanding the three types of problems covered in the script and encourages students to follow the provided link for further learning resources.
Mindmap
Keywords
💡Factorial Design
💡Two Factor Factorial Experiment
💡Levels
💡2k Factorial Design
💡Geometric Notation
💡Main Effect
💡Interaction
💡ANOVA Table
💡Degrees of Freedom
💡F-Ratio
💡Z Method
Highlights
Introduction to factorial design as a crucial topic in hypothesis testing.
Explanation of two-factor factorial experiments as a foundation for more complex designs.
Extension to 2k factorial designs involving k factors with two levels each.
Description of the levels in factorial designs, including qualitative and quantitative forms.
Calculation of combinations in a 2k factorial design using 2 raised to the power of k.
Use of geometric notation for representing high and low levels in factorial designs.
Definition of main effects and interaction effects in factorial designs.
Construction of an ANOVA table for analyzing the impact of factors in experiments.
Methods for calculating sum of squares for factors and interactions in ANOVA.
Introduction of the Z-method as an alternative approach for calculating contrasts in factorial designs.
Explanation of how to find the degrees of freedom in factorial designs.
Procedure for creating a table for factorial design with examples of notation.
Discussion on the significance of equal numbers of positive and negative levels per factor.
Calculation of F-ratios and comparison with critical values for hypothesis testing.
Identification of main and interaction effects through mean sums and division by degrees of freedom.
Application of factorial design concepts through three different examples.
Use of the Z-method for simplifying calculations in complex 2k factorial designs.
Final remarks on the importance of understanding factorial designs for hypothesis testing.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: