7.1.1 Solving a System of Equations Using Substitution

Justin Backeberg
28 Mar 202008:30
EducationalLearning
32 Likes 10 Comments

TLDRThis video script presents a comprehensive guide on solving systems of equations using the substitution method. The host, Mr. Banker, walks through three distinct problems, each involving a system of equations. The first involves finding an x and y pair that satisfies two linear equations, the second determines the dimensions of a rectangular garden with a given perimeter and area, and the third solves for x and y using two functions, one of which is a cubic equation. By substituting values and simplifying, the host demonstrates how to isolate variables and find solutions, providing clear explanations and step-by-step instructions that are easy to follow.

Takeaways
  • 📚 The video discusses solving systems of equations using the substitution method.
  • 🔢 The first system of equations presented is 2x - y = 10 and 3x + 2y = 1.
  • 🎯 The goal is to find the x and y pair that satisfies both equations simultaneously.
  • 🌟 The video chooses to isolate y in the first equation, resulting in y = 2x - 10.
  • 🔄 Substitution is used by replacing y in the second equation with the expression found in the first equation.
  • 🧠 This leads to the equation 3x + 2(2x - 10) = 1, which simplifies to 7x - 20 = 1.
  • 📈 Solving for x gives x = 3 after moving 20 to the right side and dividing by 7.
  • 🔄 Using the value of x found, the video substitutes it into the first equation to find the associated y value, resulting in y = -4.
  • 💡 The final solution for the first system of equations is the ordered pair (3, -4).
  • 📐 The video also discusses finding the dimensions of a rectangular garden with a given perimeter and area, leading to a quadratic equation.
  • 🛠️ The quadratic formula is used to solve for the width (w) and length (l) of the garden, resulting in two possible solutions for w and l.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is solving a system of equations using the substitution method.

  • What are the two equations given in the video?

    -The two equations given are 2x - y = 10 and 3x + 2y = 1.

  • Which variable does the video suggest isolating first?

    -The video suggests isolating y first due to its easier isolation in the top equation.

  • How is the first equation transformed to isolate y?

    -The first equation is transformed by subtracting 2x from both sides and then dividing by -1 to get y = 2x - 10.

  • What is the substitution step in solving the system of equations?

    -The substitution step involves replacing y in the second equation with the expression found from the first equation, which is 2x - 10.

  • What is the final x and y value of the solution?

    -The final solution is the ordered pair (3, -4).

  • How does the video introduce the problem of finding the dimensions of a rectangular garden?

    -The video introduces the problem by stating that the garden has a perimeter of 100 feet and an area of 300 square feet.

  • What are the formulas used for the perimeter and area of a rectangle?

    -The perimeter formula is 2L + 2W, and the area formula is L * W, where L is the length and W is the width of the rectangle.

  • How does the video solve for the width (W) in the garden problem?

    -The video solves for W by setting up the quadratic equation W^2 - 50W + 300 = 0 and using the quadratic formula to find the values of W.

  • What are the two possible width values for the garden?

    -The two possible width values are approximately 40.33 and 6.97.

  • What is the second system of equations discussed in the video?

    -The second system of equations discussed is y = x^3 - 6x and y = 3x.

  • How are the solutions for the second system of equations found?

    -The solutions are found by equating the expressions for y in both equations, simplifying the resulting cubic equation, and then solving for x and y using factoring and substitution.

Outlines
00:00
📚 Solving Systems of Equations Using Substitution

This paragraph introduces the method of solving a system of equations using substitution. The system consists of two equations: 2x - y = 10 and 3x + 2y = 1. The goal is to find the x and y ordered pair that satisfies both equations simultaneously. The video demonstrates isolating the variable y in the first equation, substituting it into the second equation, and solving for x. After finding the x value, the video shows how to use the first equation to find the corresponding y value, resulting in the solution (3, -4). The paragraph also discusses finding the dimensions of a rectangular garden with a given perimeter and area, using a similar substitution approach to solve for the length and width.

05:04
📈 Solving Quadratic Equations and Systems with Isolated Variables

This paragraph focuses on solving a system of equations with one quadratic and one linear equation: y = x^3 - 6x and y = 3x. The video explains how to substitute the expression for y from the linear equation into the quadratic equation to obtain a polynomial equation. After simplifying and factoring the equation, the video demonstrates solving for x by setting each factor equal to zero. Once the x values are found, the video shows how to use the linear equation to find the corresponding y values, resulting in three ordered pairs: (0, 0), (-3, -9), and (3, 9). The paragraph emphasizes the process of substitution and factoring as key steps in solving these types of equations.

Mindmap
Keywords
💡System of Equations
A system of equations refers to a set of mathematical equations that are meant to be solved simultaneously. In the context of the video, the system consists of two equations involving variables x and y, where the goal is to find the values of x and y that satisfy both equations at the same time. This is a fundamental concept in algebra and is essential for understanding the methods demonstrated in the video for solving such systems.
💡Substitution
Substitution is a mathematical method used to solve a system of equations by replacing one variable in one equation with its equivalent expression from the other equation. In the video, after isolating y in the first equation, the presenter substitutes this expression for y in the second equation, allowing them to solve for x. This technique simplifies the system and helps in finding the solution more efficiently.
💡Isolate a Variable
Isolating a variable is the process of simplifying an equation to express a single variable in terms of the other variables. This is a crucial step in solving systems of equations, as it allows us to eliminate one variable and focus on the other. In the video, the presenter chooses to isolate y in the first equation, which simplifies the process of finding the solution to the system.
💡Ordered Pair
An ordered pair is a pair of numbers, typically denoted as (x, y), where the first number represents the value of one variable and the second number represents the value of another. In the context of the video, the ordered pair represents the solution to the system of equations, where x and y are the values that satisfy both equations simultaneously.
💡Perimeter
Perimeter refers to the total length around a shape, such as a rectangle or a circle. In the video, the presenter discusses a rectangular garden with a given perimeter, which is the sum of all its sides. Understanding the concept of perimeter is essential for solving the problem of finding the garden's dimensions.
💡Area
Area is a measure of the amount of space inside a two-dimensional shape, such as a rectangle or a square. In the video, the concept of area is used to set up an equation for the rectangular garden, where the area is equal to the product of its length and width. Solving for the area is necessary to find the dimensions of the garden.
💡Quadratic Equation
A quadratic equation is a polynomial equation of degree two, which typically takes the form ax^2 + bx + c = 0. These equations represent parabolas and are solved using methods such as factoring, completing the square, or the quadratic formula. In the video, the presenter encounters a quadratic equation while trying to find the dimensions of the garden and uses the quadratic formula to find the solutions.
💡Quadratic Formula
The quadratic formula is a general method for solving quadratic equations and is given by the formula: -b ± √(b^2 - 4ac) / (2a). It provides the solutions for x when an equation is in the form ax^2 + bx + c = 0. In the video, the quadratic formula is used to find the width (W) of the garden when the equation relating the perimeter and area is set to zero.
💡Factoring
Factoring is the process of breaking down a polynomial into a product of other polynomials or factors. It is a common method for solving quadratic equations when they can be easily factored. In the video, the presenter factors a cubic equation to simplify it and find the solutions for x.
💡Difference of Squares
The difference of squares is a special factoring pattern where a polynomial is expressed as the difference of two perfect squares. It takes the form a^2 - b^2, which can be factored into (a + b)(a - b). In the video, the cubic equation is a difference of squares after factoring out the common factor x, allowing the presenter to find the solutions for x.
💡Greatest Common Factor (GCF)
The greatest common factor (GCF) is the largest number or term that can divide all the terms in a polynomial expression without leaving a remainder. Factoring out the GCF simplifies the expression and can help in solving equations. In the video, the GCF of x is factored out from the expression x^2 - 9, leading to the difference of squares.
Highlights

The video discusses solving a system of equations using the substitution method.

The system of equations consists of 2x - y = 10 and 3x + 2y = 1.

The goal is to find the x and y ordered pair that satisfies both equations simultaneously.

The video chooses to isolate y in the first equation for the substitution method.

The first equation is transformed to y = 2x - 10 after substituting and simplifying.

The second equation is solved by substituting y with 2x - 10 and simplifying to get 7x = 21.

The value of x is found to be 3 by dividing both sides by 7.

The associated y value is found to be -4 by substituting x = 3 into the first simplified equation.

The final solution is the ordered pair (3, -4).

The video then discusses finding the dimensions of a rectangular garden with a given perimeter and area.

The perimeter is 100 feet and the area is 300 square feet.

The equations for the perimeter and area of a rectangle are 2L + 2W = P and A = L * W, respectively.

The video solves for the length and width of the garden using the quadratic formula.

Two possible width values are found, approximately 40.3 and 6.97, after solving the quadratic equation.

The corresponding length values are approximately 6.97 and 40.3, depending on which value is chosen for the width.

The video concludes with another system of equations where y = x^3 - 6x and y = 3x.

By substituting 3x for y in the first equation, a cubic equation is formed which is then factored.

The factored equation yields three x values: 0, -3, and 3.

The corresponding y values for these x values are 0, -9, and 9, resulting in ordered pairs (0, 0), (-3, -9), and (3, 9).

The video wraps up by summarizing the process and thanking viewers for watching.

Transcripts

Browse More Related Video

Solving Systems of Equations By Elimination & Substitution With 2 Variables

PROBLEMS INVOLVING SYSTEM OF NONLINEAR EQUATIONS || PRECALCULUS

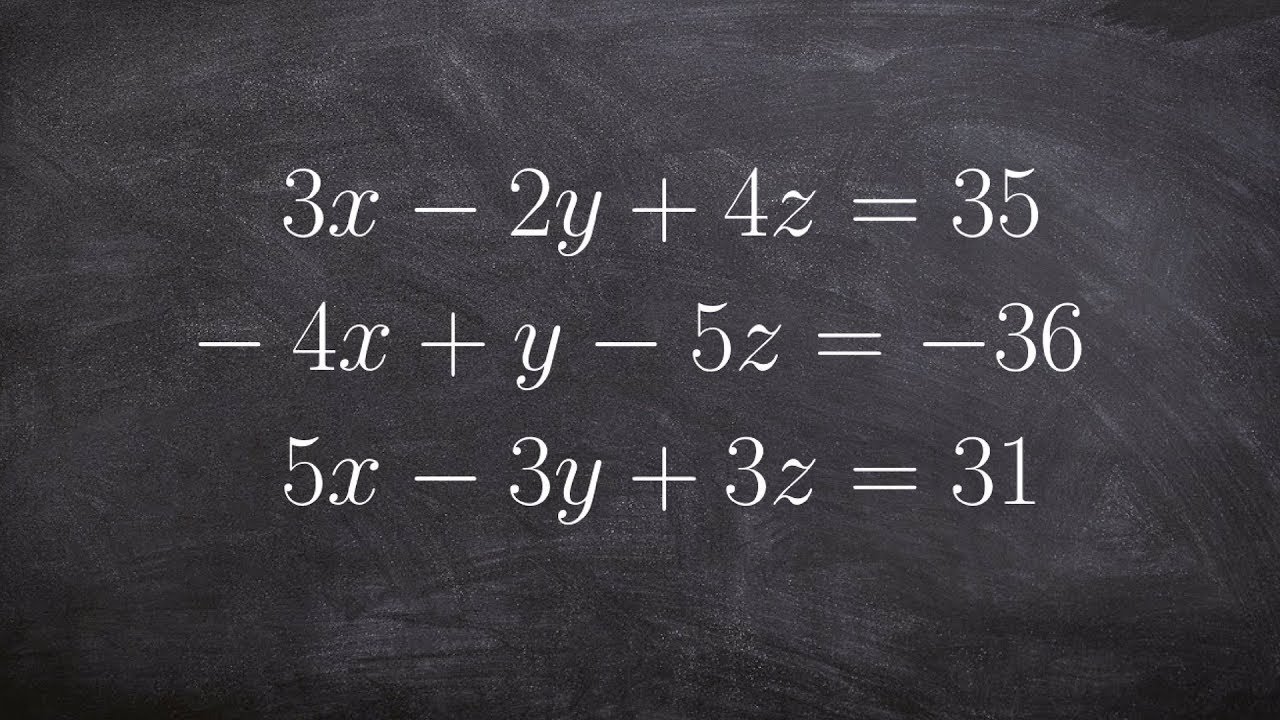
Solve a system with three variables

Separable First Order Differential Equations - Basic Introduction

Substitution Method For Solving Systems of Linear Equations, 2 and 3 Variables, Algebra 2

Cramer's Rule - 2x2 & 3x3 Matrices - Solving Systems of Linear Equations - 2 & 3 Variables

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Equation SolvingSubstitution MethodMathematics TutorialEducational ContentProblem-Solving SkillsAlgebra TechniquesVideo InstructionMath LearningInteractive TeachingOnline Education