7.2.0 Estimating a Population Mean - Lesson Overview, Key Concepts, Learning Outcomes

Sasha Townsend - Tulsa
30 Oct 202004:15
EducationalLearning
32 Likes 10 Comments

TLDRThis video lesson overview introduces Lesson 7.2, focusing on estimating the population mean using sample data. It covers point estimation with the sample mean as the best estimator, constructing confidence intervals for the mean in cases where the population standard deviation is known or unknown, and determining the sample size needed for a desired margin of error and confidence level. The lesson also explores the student's t-distribution characteristics and finding critical t-values, essential for estimating the population mean accurately.

Takeaways
  • 📚 The lesson is an overview of Lesson 7.2 focusing on estimating the population mean using sample data.
  • 🔍 The script is based on slides from Pearson and modified for the course, referencing 'Essentials of Statistics' by Mario Triola.
  • 🎯 Lesson 7.1 covered estimating the population proportion, while 7.2 shifts the focus to estimating the population mean.
  • 📈 The sample mean (x̄) is identified as the best point estimate for the population mean (μ), with an explanation to follow.
  • 📊 Two methods for estimating the population mean are discussed: point estimate and confidence interval.
  • 🤔 The common case of estimating the population mean is addressed when the population standard deviation is unknown.
  • 📉 A rare case is also mentioned where the population standard deviation is known.
  • 🔎 The importance of determining the sample size for a desired margin of error and confidence level is highlighted.
  • 📝 Learning outcomes include understanding the student's t-distribution, finding critical t-values, and estimating the population mean with confidence intervals.
  • 📚 The script outlines the process of interpreting and finding confidence intervals for the population mean when the standard deviation is unknown.
  • 📋 The final learning outcome involves calculating the necessary sample size for a given desired accuracy and confidence level when the standard deviation is known or can be estimated.
Q & A

  • What is the main focus of Lesson 7.2?

    -Lesson 7.2 focuses on estimating the population mean using sample data, including point estimates and confidence intervals.

  • What are the two methods discussed in Lesson 7.2 for estimating the population mean?

    -The two methods discussed are point estimation and estimation using a confidence interval.

  • Why is the sample mean, x-bar, considered the best point estimate for the population mean, mu?

    -The sample mean, x-bar, is considered the best point estimate for the population mean, mu, because it is the most unbiased estimator and it reflects the center of the sample data.

  • In what two cases will the lesson discuss estimating the population mean with a confidence interval?

    -The lesson will discuss estimating the population mean with a confidence interval in two cases: when the population standard deviation is unknown and when it is known.

  • What is the importance of determining the sample size for estimating a population mean?

    -Determining the sample size is important because it helps to ensure that the desired margin of error and confidence level are achieved, which is crucial for the accuracy and reliability of the confidence interval.

  • What is the significance of the student t-distribution in the context of this lesson?

    -The student t-distribution is significant because it is used to find critical values when the population standard deviation is unknown, which is the more common case in estimating the population mean.

  • What is a critical value t-sub-alpha-over-2 and how is it used in this lesson?

    -A critical value t-sub-alpha-over-2 is a value from the t-distribution that corresponds to a given confidence interval. It is used to construct the confidence interval for the population mean.

  • What are the learning outcomes of Lesson 7.2 related to the student t-distribution and confidence intervals?

    -The learning outcomes include understanding the characteristics of the student t-distribution, finding a critical value t-sub-alpha-over-2, estimating the population mean with a point estimate and a confidence interval, interpreting confidence intervals, and finding the sample size necessary for a desired margin of error and confidence level.

  • How does the process of estimating the population mean differ when the population standard deviation is known compared to when it is unknown?

    -When the population standard deviation is known, the process involves using the z-distribution instead of the t-distribution. The calculations for the margin of error and confidence interval will differ slightly due to the use of different distribution properties.

  • What is the purpose of learning to interpret and find confidence intervals for the population mean?

    -The purpose is to provide a range of values within which the true population mean is likely to fall, given a certain level of confidence. This helps in making informed decisions based on the sample data.

  • How will the lesson help students understand the relationship between sample size, margin of error, and confidence level?

    -The lesson will guide students through the process of calculating the necessary sample size to achieve a desired margin of error and confidence level, emphasizing the importance of these factors in accurate statistical estimation.

Outlines
00:00
📚 Lesson Overview for Estimating Population Mean

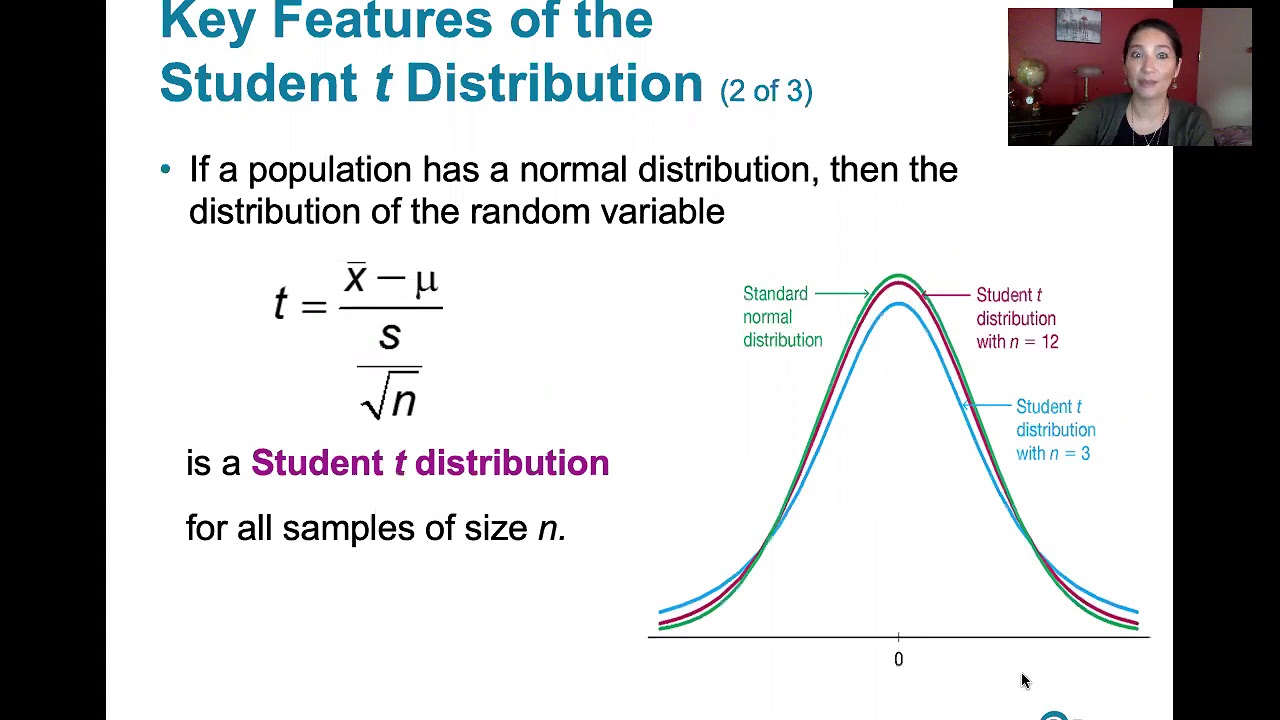
This paragraph introduces Lesson 7.2, focusing on estimating the population mean using sample data. It is based on the second section of Chapter 7 from 'Essentials of Statistics' by Mario Triola. The lesson builds on the previous one, 7.1, which covered estimating the population proportion, and now shifts the focus to the mean. The instructor emphasizes the importance of understanding how to estimate the mean with both a point estimate and a confidence interval, especially when the population standard deviation is unknown, which is the more common scenario. The learning outcomes for the lesson are outlined, including understanding the student t-distribution, finding critical t-values, and determining the sample size needed for a desired margin of error and confidence level.

Mindmap
Keywords
💡Population Mean
The population mean, often denoted by the Greek letter mu (μ), is the average value of a population. It is a key concept in statistics and serves as the central value around which all other data points are distributed. In the video, the focus is on estimating the population mean using sample data, which is a common practice when the entire population is too large to measure directly. The script mentions estimating the population mean with both a point estimate and a confidence interval.
💡Point Estimate
A point estimate is a single value that serves as the best guess for an unknown parameter, in this case, the population mean. The script emphasizes that the sample mean (x̄) is considered the best point estimate for the population mean, as it is the single value derived from the sample data that most closely represents the mean of the entire population.
💡Sample Mean (x̄)
The sample mean, denoted as x̄, is the average of the values in a sample. It is used as an estimator for the population mean. The script explains that the sample mean is calculated by summing all the values in the sample and dividing by the number of observations, and it is the best point estimate for the population mean μ.
💡Confidence Interval
A confidence interval is a range of values, derived from a sample, that is likely to contain the population parameter with a certain level of confidence. The video discusses how to estimate the population mean using a confidence interval, which provides a range rather than a single point estimate, reflecting the uncertainty in the estimate.
💡Population Standard Deviation
The population standard deviation is a measure of the amount of variation or dispersion in a set of values in the entire population. In the script, it is mentioned that estimating the population mean involves two cases: when the population standard deviation is unknown and when it is known. The known case is considered rare, while the unknown case is more common.
💡Sample Size
Sample size refers to the number of observations or elements included in a sample. The script discusses the importance of determining the appropriate sample size to achieve a desired margin of error and level of confidence when estimating the population mean, especially when the population standard deviation is known or can be estimated.
💡Margin of Error
The margin of error is the range within which the true population parameter is estimated to lie, with a certain level of confidence. The script explains that knowing the desired margin of error is crucial for determining the sample size needed to achieve a confidence interval that includes the true population mean.
💡Student's t-Distribution
Student's t-distribution is a type of probability distribution used when estimating a population parameter from a sample, particularly when the population standard deviation is unknown. The script mentions that the characteristics of the Student's t-distribution change with the sample size, and it is used to find critical values for constructing confidence intervals.
💡Critical Value (t_alpha/2)
A critical value, specifically t_alpha/2, is a value from the t-distribution that determines the boundaries of the confidence interval. The script explains that finding this critical value is a necessary step in constructing a confidence interval for the population mean when the population standard deviation is unknown.
💡Essentials of Statistics
Essentials of Statistics is the textbook by Mario Triola that the video's lesson is based on. The script mentions that the lesson is derived from the second section of chapter 7 of the 6th edition of this book, which covers estimating parameters and determining sample sizes.
💡Desired Level of Confidence
The desired level of confidence is the probability that the confidence interval will contain the true population parameter. The script discusses how to calculate the sample size necessary to achieve a specific level of confidence in the estimate of the population mean, which is an important aspect of statistical inference.
Highlights

Lesson 7.2 focuses on estimating the population mean using sample data.

The lesson is based on the second section of Chapter 7 from the textbook 'Essentials of Statistics' by Mario Triola.

In 7.1, students learned to estimate the population proportion with point estimates and confidence intervals.

Lesson 7.2 will focus on estimating the population mean in a similar manner.

The sample mean (x-bar) is the best point estimate for the population mean (mu).

The reason why x-bar is the best point estimate will be explained later in the lesson.

Two methods will be used to estimate the population mean: point estimate and confidence interval.

The more common case is when the population standard deviation is unknown.

A rare case is when the population standard deviation is known.

Students will learn how to find the sample size needed to estimate the population mean with a desired margin of error and confidence level.

Being able to determine the sample size is important for collecting the right amount of data to achieve the desired margin of error and confidence interval.

The characteristics of the student t-distribution will be discussed, which changes shape based on the sample size.

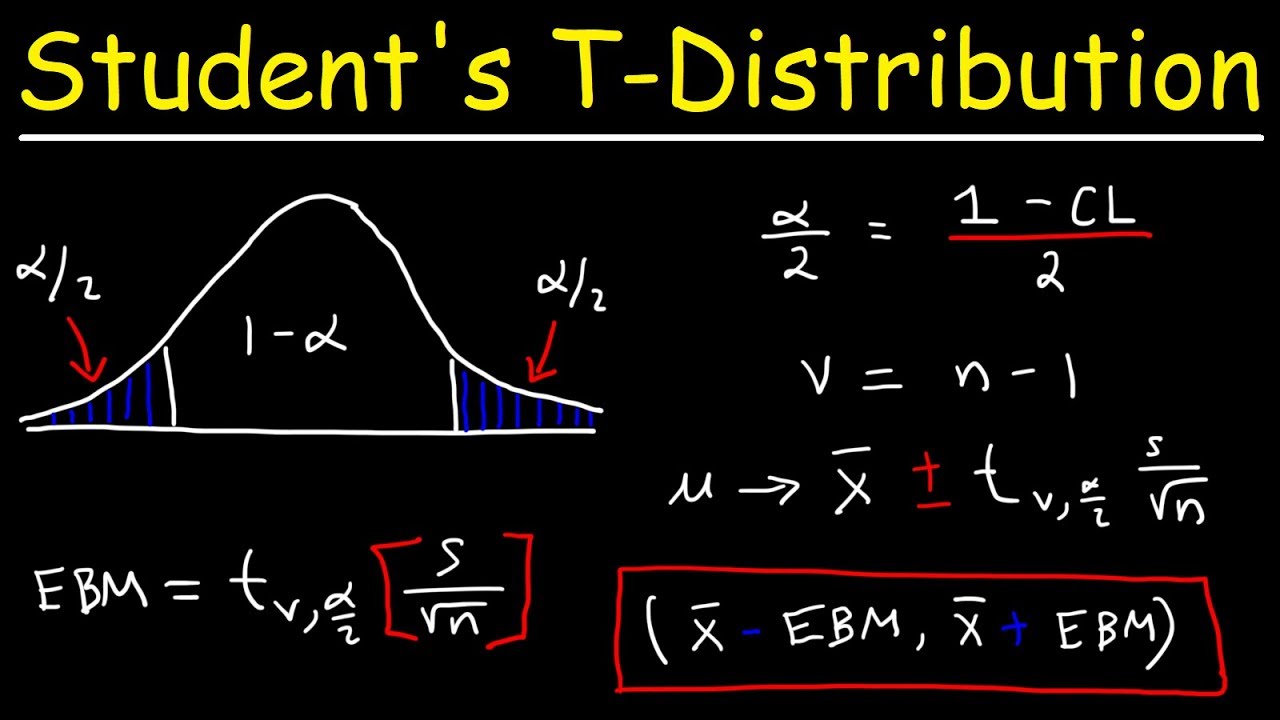
Students will learn to find the critical value t(α/2) for a given confidence interval.

The sample mean is the best point estimate of the population mean and will be explained in detail.

Confidence intervals for the population mean will be interpreted and calculated in situations where the population standard deviation is not known.

Students will learn to find the margin of error and point estimate (x-bar) for the population mean given a confidence interval.

The sample size necessary to estimate the population mean with a desired degree of accuracy and confidence level will be calculated, especially when the population standard deviation is known or can be estimated.

A confidence interval for the population mean will be interpreted in the uncommon situation when the population standard deviation is known, with minor adjustments compared to the unknown standard deviation case.

Transcripts

Browse More Related Video

7.2.1 Estimating a Population Mean - Student t Distribution and Finding Critical t Values

7.2.4 Estimating a Population Mean - Sample Size for a Desired Margin of Error and Confidence Level

Elementary Statistics - Chapter 7 - Estimating Parameters and Determining Sample Sizes Part 2

Student's T Distribution - Confidence Intervals & Margin of Error

Introduction to the t Distribution (non-technical)

Confidence Intervals | Population Mean: σ Unknown

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Population MeanEstimationStatisticsConfidence IntervalSample SizeMario TriolaEssentialsInferenceStudent TData Analysis