This Is the Calculus They Won't Teach You
TLDRThe development of calculus is a rich tapestry woven over millennia, involving the struggle with infinity and the interplay of ideas between algebra, geometry, and physics. From Archimedes' careful approach to infinitesimal concepts to the revolutionary work of Descartes in analytic geometry, the stage was set for the groundbreaking contributions of Newton and Leibniz. Their work, though not without controversy, laid the foundation for modern calculus, highlighting the power of relationships between ideas and people. The narrative underscores the importance of understanding the historical context of mathematical concepts to truly appreciate their significance and relevance in our world.
Takeaways
- 🌌 The concept of infinity is daunting and has been challenging for mathematicians throughout history.
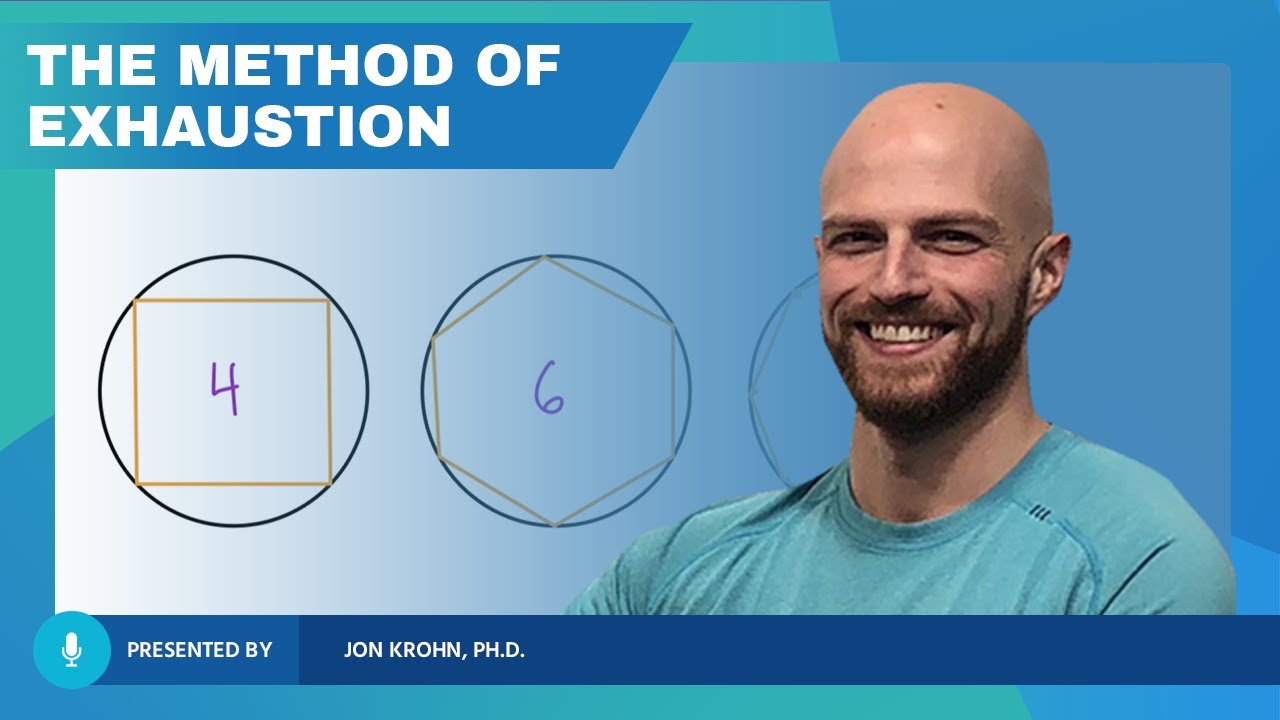
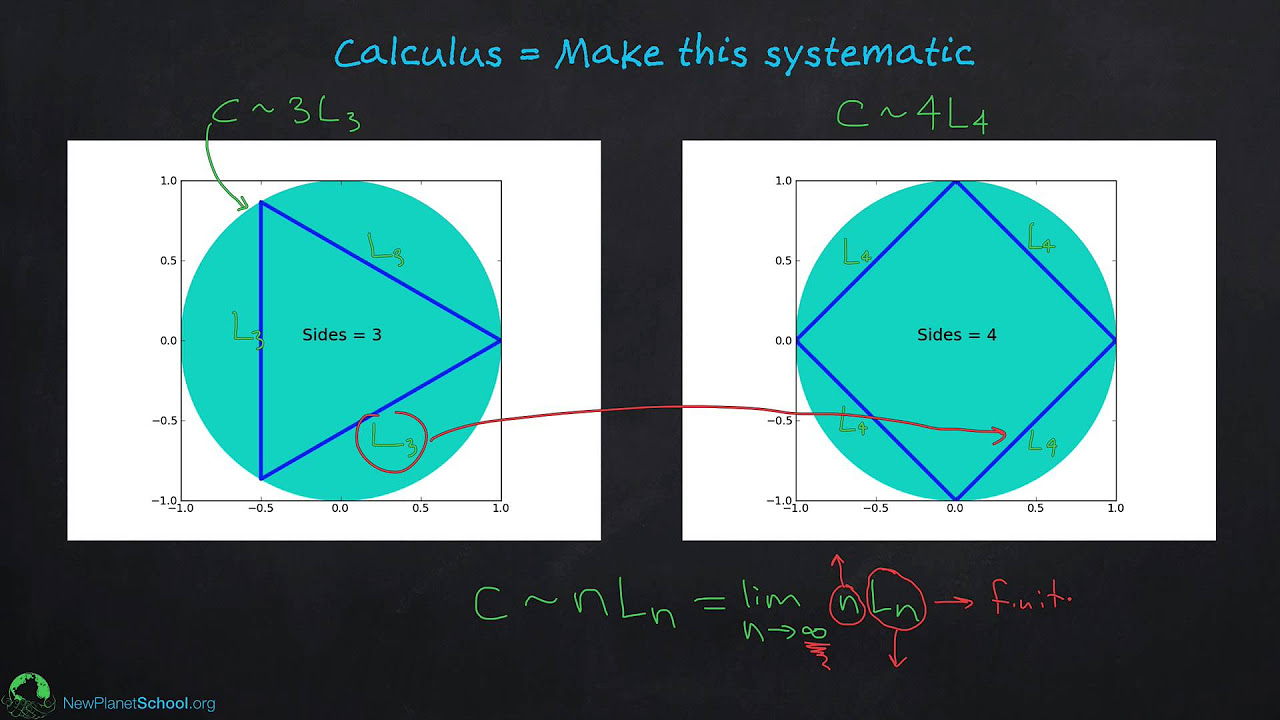
- 🔢 The ancient Greeks, such as Archimedes, made significant strides in understanding shapes and areas using the concept of infinitesimals without actually using infinity.
- 📚 The development of algebra was crucial to the advancement of calculus, with early contributions from scholars like Al-Khwarizmi.
- 📐 Descartes' invention of the coordinate system revolutionized mathematics by combining geometry and algebra, allowing for the analysis of curves using equations.
- 🌟 The work of Galileo and Kepler marked the transition from pure to applied mathematics, using math to model physical phenomena like gravity.
- 💡 Isaac Newton and Gottfried Wilhelm Leibniz independently developed calculus, with Leibniz being the first to publish his work and popularize the subject.
- 📈 Calculus has its roots in many pairs of ideas and people, showcasing the power of interdisciplinary thinking and collaboration.
- 📚 The concept of limits was introduced to calculus as a way to handle infinite processes without directly invoking infinity.
- 🔄 The historical progression of calculus is important for understanding its concepts and the struggle mathematicians faced in its development.
- 🎓 Incorporating the history of calculus into teaching can improve students' understanding and appreciation of the subject.
- 🚀 The development of calculus has been a journey of grappling with infinity, leading to its refinement and the establishment of rigorous mathematical foundations.
Q & A
What is the significance of the number 'a Google' in the context of the script?
-The term 'a Google' is used to describe an unimaginably large number, which is still dwarfed by the concept of infinity. It illustrates the vastness of numbers and the challenge in comprehending the infinite.
How does the script use the example of the observable universe to put the concept of large numbers into perspective?
-The script mentions that the observable universe is about 93 billion light years in diameter. Even when expressed in terms of the smallest unit of distance, Plank length, this number is still incomparable to the concept of 'a Google' or infinity, highlighting the enormity of these scales.
What is the historical significance of Archimedes' work in the development of calculus?
-Archimedes' work on calculating the area of a circle using infinitesimally small slices is an early example of integration in calculus. His method of reasoning and proving geometric areas using the concept of infinity laid foundational ideas for later calculus development.
How did the ancient Greeks view the concept of infinity?
-The ancient Greeks found the concept of infinity paradoxical. They struggled with the idea of taking an infinite number of steps to reach a point, as they believed it was impossible to complete an infinite process.
What role did algebra play in the development of calculus?
-The development of algebra was crucial to calculus as it provided a systematic way to manipulate and solve equations. The introduction of letters as symbols for unknowns and constants was a key step that allowed for the expression and analysis of functions, which are central to calculus.
How did Descartes contribute to the development of calculus with his analytic geometry?
-Descartes introduced the coordinate system, which combined geometry and algebra. This allowed mathematicians to analyze curves and shapes using equations, providing a visual representation of relationships between variables and laying the groundwork for the study of derivatives and integrals in calculus.
What is the fundamental theorem of calculus and why is it important?
-The fundamental theorem of calculus establishes the relationship between differentiation and integration. It states that every integral corresponds to a unique derivative, and vice versa. This theorem is crucial as it unifies the two main branches of calculus and provides a powerful tool for solving a wide range of mathematical and physical problems.
How did Newton and Leibniz contribute to the development of calculus?
-Both Newton and Leibniz independently developed calculus, with each focusing on different aspects. Newton worked on the concepts of rates of change and areas under curves, while Leibniz focused on the notation and publication of calculus methods. Despite their different approaches, both recognized the importance of infinitesimals in their work, even though they were aware of the philosophical challenges this presented.
What is the concept of limits and how does it help in understanding calculus?
-The concept of limits provides a rigorous way to talk about the behavior of functions as they approach certain values without actually reaching them. In calculus, limits are used to define derivatives and integrals without directly invoking infinity, thus providing a more solid foundation for the subject.
Why is the historical context important for understanding calculus?
-Understanding the historical context of calculus helps to appreciate the evolution of mathematical ideas and the struggles mathematicians faced in developing these concepts. It also humanizes the subject, making it more relatable and engaging for students, and provides motivation for learning the subject beyond just mastering the techniques.
What is the debate surrounding the concept of infinity in mathematics?
-The debate surrounding infinity in mathematics involves questions about its existence and its role in the foundation of math. Some argue that calculus can work fine with infinitesimals, while others claim that infinity doesn't exist and that the current mathematical foundations that involve infinity are flawed.
Outlines
🌌 The Vastness of Numbers and Infinity
This paragraph introduces the concept of incredibly large and small numbers, comparing them to the observable universe's size and Planck length. It discusses the human struggle to comprehend the concept of infinity, as exemplified by the fear it can instill. The paragraph also raises questions about why humans engage with such powerful ideas like infinity in mathematics, particularly within calculus, and sets the stage for exploring the historical development of calculus.
📚 Ancient Greek Mathematics and the Birth of Calculus
The paragraph delves into the early stages of calculus, highlighting the contributions of ancient Greeks like Archimedes. It explains how Archimedes used the concept of infinitely small slices to calculate the area of a circle, which is a precursor to integration. The text also touches on the development of algebra and the importance of Hindu-Arabic numerals, setting the foundation for more advanced mathematical concepts that would lead to the formalization of calculus.
🌟 The Evolution of Algebra and Analytic Geometry
This section discusses the crucial development of algebra and analytic geometry, which were essential for the advancement of calculus. It describes how algebraic notation evolved, with figures like Al-Khwarizmi and Descartes contributing to the field. The paragraph also explains how Descartes' coordinate system revolutionized the way mathematicians could analyze curves and relationships between variables, marking a significant step towards modern calculus.
🚀 The Connection Between Differentiation and Integration
The paragraph explores the historical development of calculus, focusing on the connection between differentiation and integration. It mentions the work of scholars like Cavalieri and Torricelli, who used infinitesimals to find volumes of solids. The text then transitions to the contributions of Galileo and Kepler, who applied mathematical concepts to model physical phenomena, such as gravity, marking the beginning of the relationship between calculus and physics.
💡 Newton, Leibniz, and the Birth of Modern Calculus
This section details the pivotal roles of Isaac Newton and Gottfried Leibniz in the development of calculus. It explains how both independently discovered the fundamental theorem of calculus but approached it differently, with Leibniz focusing on differentials and Newton on rates of change. The paragraph also discusses the controversy surrounding their work and how Leibniz's social skills helped popularize calculus, despite the initial lack of rigorous foundations.
📚 The Limit: Refining the Concept of Infinity in Calculus
The paragraph discusses the concept of limits as a way to handle infinity in calculus without directly invoking it. It explains how limits provide a rigorous foundation for calculus by allowing mathematicians to express infinite processes without actually dealing with infinite numbers. The text also touches on the historical development of limits and their importance in the evolution of calculus into a more rigorous field known as analysis.
🌉 The Importance of Historical Context in Teaching Calculus
This final paragraph emphasizes the importance of teaching calculus with historical context to help students understand the development of its concepts. It discusses the struggles mathematicians faced with infinity and how understanding this history can inform modern teaching methods. The text suggests that incorporating the story of calculus can motivate students and provide a deeper understanding of the subject, ultimately changing their perspective on the importance and relevance of calculus.
Mindmap
Keywords
💡Infinity
💡Calculus
💡Integral
💡Derivative
💡Limits
💡Algebra
💡Analytic Geometry
💡Archimedes
💡Newton
💡Leibniz
💡History of Mathematics
Highlights
The concept of infinity and its relation to calculus is explored, highlighting the challenges in understanding such a vast concept.
The observable universe's size is compared to a 'googleplex', a humorously large number, to illustrate the scale of mathematical concepts.
The ancient Greeks' approach to understanding the concept of infinity and its paradoxes is discussed, including Archimedes' work on the area of a circle.
The development of algebra and its crucial role in the advancement of calculus is mentioned, with the works of Al-Khwarizmi and others.
René Descartes' invention of the coordinate system and its revolutionary impact on analytic geometry is highlighted.
The concept of instantaneous rate of change is traced back to Zeno's paradox and its practical applications in the works of Aryabhata.
The development of integral calculus is discussed, with Bonaventura Cavalieri's controversial method of 'indissolubles' and Evangelista Torricelli's work.
Galileo Galilei's and Johannes Kepler's contributions to the understanding of motion and gravity are noted, marking the transition to applied mathematics.
Isaac Newton's and Gottfried Wilhelm Leibniz's independent development of calculus and their contrasting approaches to infinitesimals are compared.
Leibniz's role in popularizing calculus through his diplomatic missions and networking is emphasized.
The fundamental theorem of calculus is introduced, connecting integration and differentiation in a groundbreaking way.
The use of limits in calculus is explained as a way to avoid direct engagement with infinity, providing a rigorous foundation.
The historical progression of calculus is argued to be important for students to understand the development and significance of mathematical concepts.
The debate over the existence and use of infinity in mathematics is mentioned, indicating ongoing discussions among mathematicians.
The potential benefits of teaching calculus with historical context are discussed, aiming to provide a more engaging and comprehensive understanding.
The video concludes with a call for a different perspective on calculus, emphasizing its humanity and the story of its development.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: