6.4.2 The Central Limit Theorem - Probabilities for a Range of Normally Distributed Sample Means
TLDRThis video lesson delves into the applications of the Central Limit Theorem (CLT), focusing on when the distribution of sample means can be approximated by a normal distribution. It outlines the criteria for applying the CLT: a normally distributed population or a sample size exceeding 30. The video explains how to calculate probabilities associated with sample means using z-scores and demonstrates the process with an example involving female pulse rates. It highlights the difference in probabilities for individual pulse rates versus the mean pulse rate of a sample, emphasizing the importance of the CLT in statistical analysis.
Takeaways
- 📚 The video discusses the application of the Central Limit Theorem (CLT) in determining if the distribution of sample means can be approximated by a normal distribution.
- 🔢 To apply the CLT, the sample size must be greater than 30, or the population must have a normal distribution.
- 📉 If the requirements for CLT are not met, other methods exist but are not covered in this section of the lesson.
- 🌟 A large sample size (n > 30) or a normally distributed population ensures that the sample means are well-approximated by a normal distribution.
- 📉 The mean of the distribution of sample means is equal to the population mean, and the standard deviation is the population standard deviation divided by the square root of the sample size.
- 📊 As the sample size increases, the sample standard deviation decreases, reflecting reduced variation in the sample means.
- ➗ The z-score is used for converting sample means to standard deviations from the mean, which is crucial for computing probabilities.
- 🔍 The procedure for practical problem-solving starts with checking the requirements of the CLT and then determining whether the problem involves individual values or sample means.
- 📝 For individual values from a population, use the z-score formula with the population mean and standard deviation.
- 📐 For sample means, use the mean and standard deviation of the sample means, calculated with the population parameters.
- 📊 The z-score formula for sample means is (x̄ - μ̄) / (σ / √n), where x̄ is the sample mean, μ̄ is the population mean, σ is the population standard deviation, and n is the sample size.
- 📈 The video provides an example involving pulse rates of females, illustrating how to calculate probabilities for individual values and sample means using the normal distribution and z-scores.
Q & A
What is the main topic of the video script?
-The main topic of the video script is the application of the Central Limit Theorem (CLT) in determining whether the distribution of sample means can be approximated by a normal distribution and computing probabilities associated with a range of values for sample means.
What are the two conditions under which the Central Limit Theorem can be applied?
-The Central Limit Theorem can be applied if either the population has a normal distribution, or the sample size is greater than 30.
What happens to the sample standard deviation as the sample size increases?
-As the sample size increases, the sample standard deviation decreases, which means the variation in the sample means starts to shrink.
What is the formula for calculating the mean of the distribution of sample means?
-The mean of the distribution of sample means is equal to the mean of the original population.
How is the standard deviation of the distribution of sample means calculated?
-The standard deviation of the distribution of sample means is calculated by dividing the population standard deviation by the square root of the sample size.
What is the purpose of using a z-score in the context of the Central Limit Theorem?
-The purpose of using a z-score is to convert a sample mean into a standard number of deviations from the mean of the distribution of sample means, which allows for the computation of probabilities associated with a range of values for sample means.
How does the z-score formula for a sample mean differ from that of an individual value?
-The z-score formula for a sample mean uses the mean of the sample means and the standard deviation of the sample means, whereas the z-score for an individual value uses the population mean and the population standard deviation.
What is the first step in practical problem solving using the Central Limit Theorem?
-The first step is to check the requirements, which involves verifying that the original population has a normal distribution or that the sample size is greater than 30.
How does the video script differentiate between dealing with individual values and sample means?
-The script differentiates by using the appropriate mean and standard deviation for the distribution being considered (either the original population or the sample means) and by calculating the z-score accordingly.
Can you provide an example from the script where the Central Limit Theorem is applied to a normally distributed population?
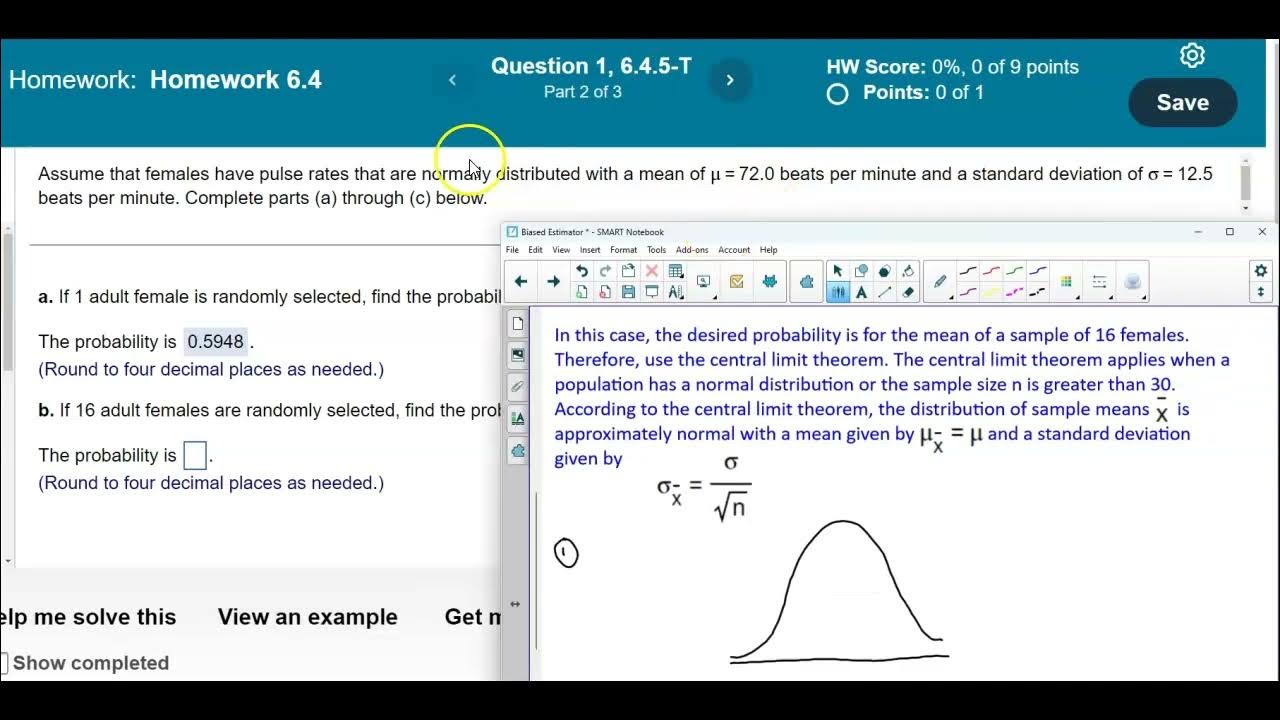
-An example given is the pulse rates of females, which are normally distributed with a mean of 74 beats per minute and a standard deviation of 12.5 beats per minute. The script discusses calculating the probability for an individual's pulse rate and the mean pulse rate of a sample of 16 females.
What is the interpretation of the probabilities calculated in the example involving female pulse rates?
-The interpretation is that there is a 66.44% chance that an individual female has a pulse rate less than 80 beats per minute, and a 97.26% chance that a sample of 16 females will have a mean pulse rate less than 80 beats per minute.
Outlines
📚 Applications of the Central Limit Theorem
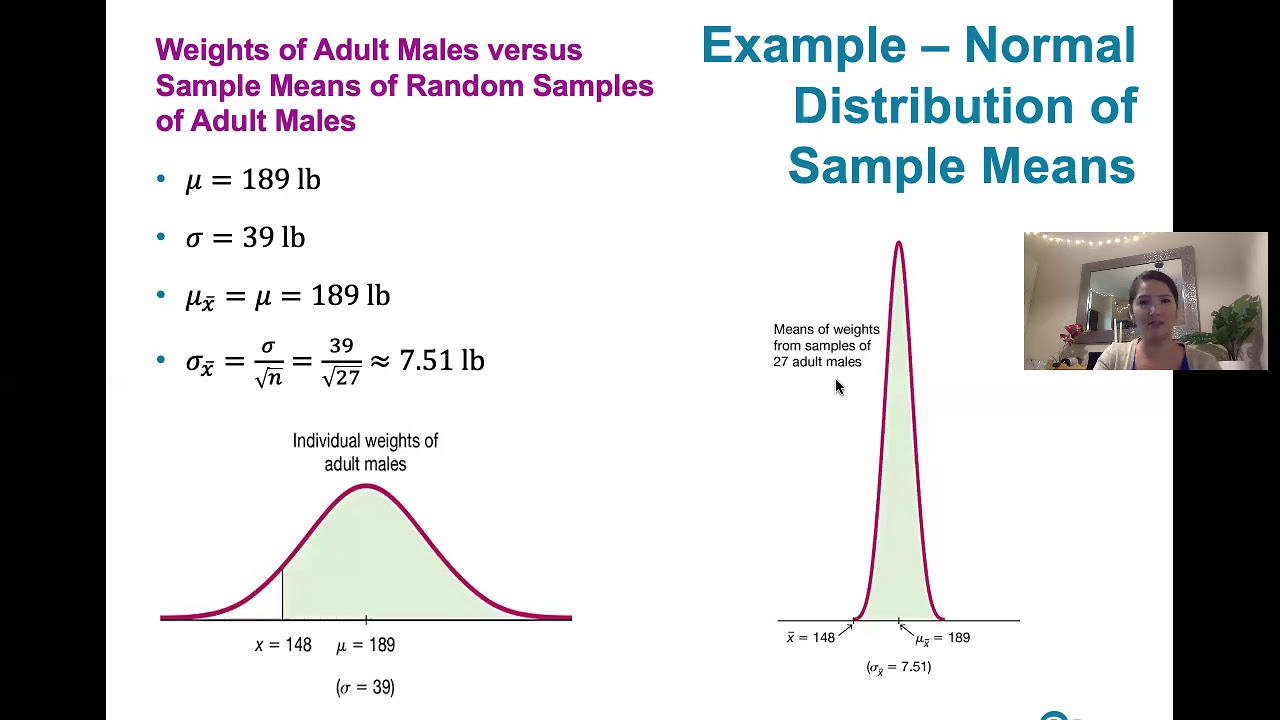
This paragraph discusses the conditions under which the central limit theorem can be applied to sample means. It explains that if the population distribution is normal or the sample size exceeds 30, the distribution of sample means can be approximated by a normal distribution. The mean of the sample means is equal to the population mean, and the standard deviation is the population standard deviation divided by the square root of the sample size. The paragraph also introduces the concept of z-scores for calculating probabilities associated with sample means and emphasizes the importance of averaging values to reduce variation as sample size increases.
📈 Probability Calculations for Sample Means
The second paragraph focuses on calculating probabilities for sample means using the central limit theorem. It provides a step-by-step guide on how to use z-scores and normal distribution tables or Excel functions to find probabilities. An example is given involving the pulse rates of females, which are normally distributed. The paragraph explains how to find the probability of an individual's pulse rate being less than 80 beats per minute and contrasts this with finding the probability of a sample mean for a group of 16 females also being less than 80 beats per minute.
📊 Using Excel for Normal Distribution Probabilities
This paragraph demonstrates how to use Excel to calculate probabilities related to the normal distribution of sample means. It continues the example of female pulse rates, showing how to use Excel's NORM.DIST function to find the probability that a sample mean of 16 randomly selected adult females is less than 80 beats per minute. The paragraph emphasizes the importance of using the correct mean and standard deviation for the sample means, which is the population standard deviation divided by the square root of the sample size.
🔍 Interpreting the Probability of Sample Means
The final paragraph interprets the results of the probability calculations for both individual pulse rates and sample means of a group. It explains that while there is a 66.44% chance that an individual female will have a pulse rate less than 80 beats per minute, there is a 97.26% chance that the mean pulse rate of a sample of 16 females will be less than 80 beats per minute. The paragraph concludes by noting the importance of the original population being normally distributed to justify the use of the central limit theorem for sample means, even when the sample size is less than 30.
Mindmap
Keywords
💡Central Limit Theorem
💡Sample Means
💡Normal Distribution
💡Sample Size
💡Population Standard Deviation
💡Z-Score
💡Probability
💡Standard Deviation of Sample Means
💡Normal Distribution Function
💡Cumulative Distribution Function
💡Pulse Rates
Highlights
The video discusses the central limit theorem's applications in determining if the distribution of sample means can be approximated by a normal distribution.
Two requirements for applying the central limit theorem: either the population has a normal distribution or the sample size is greater than 30.
If the sample size is large enough (n > 30) or the population is normally distributed, the sample means are well approximated by a normal distribution.
The mean of the distribution of sample means is equal to the population mean.
The standard deviation of the sample means is the population standard deviation divided by the square root of the sample size.
As sample size increases, the sample standard deviation decreases, indicating reduced variation.
Z-score conversion is used to compute probabilities associated with ranges of sample means.
Procedure for practical problem solving includes checking the requirements and verifying the population's normal distribution or sufficient sample size.
Different methods are required if the population is not normally distributed and the sample size is less than or equal to 30.
For individual values from the population, use the z-score formula with population parameters.
For sample means, use the mean and standard deviation of the sample means in the z-score calculation.
The relationship between standard deviation and mean simplifies the z-score formula for sample means.
Use normal distribution functions or tables to find probabilities and areas for z-scores.
Example problem involves calculating the probability of a female's pulse rate being less than 80 beats per minute.
For sample mean calculations, use the mean and standard deviation specific to the distribution of sample means.
The probability that a sample of 16 females has a mean pulse rate less than 80 beats per minute is calculated using the central limit theorem.
The video provides a step-by-step guide on using Excel for normal distribution calculations.
Interpretation of results shows a higher probability for the mean pulse rate of a sample being less than 80 compared to an individual's pulse rate.
The central limit theorem's assumptions are crucial for the validity of the calculations and conclusions drawn.
Transcripts
Browse More Related Video
6.4.1 The Central Limit Theorem - What the Central Limit Theorem Says and What It Doesn't Say
Math 14 HW 6.4.5-T Using the Central Limit Theorem

02 - What is the Central Limit Theorem in Statistics? - Part 1

The Central Limit Theorem, Clearly Explained!!!
Introduction to the Central Limit Theorem

Elementary Stats Lesson #13
5.0 / 5 (0 votes)
Thanks for rating: