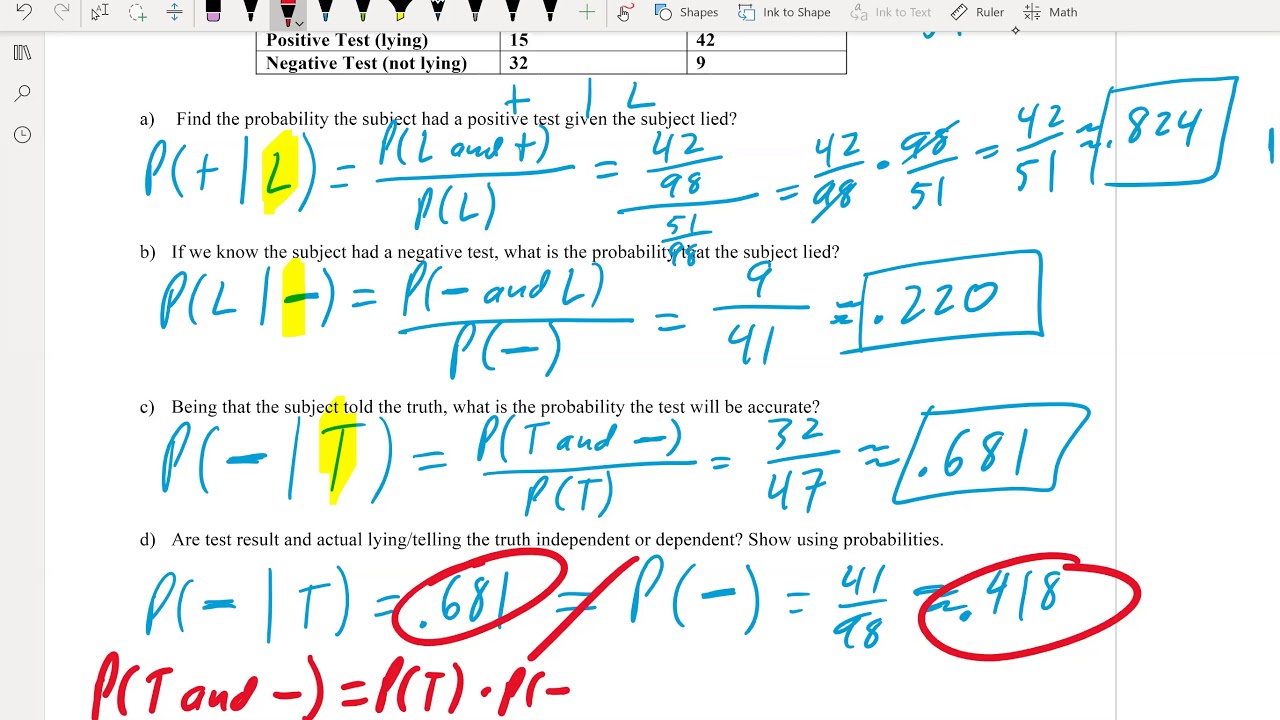
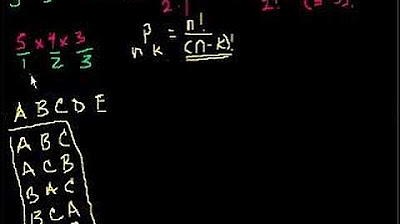4.4.2 Counting - The Factorial Rule
TLDRIn this video, the focus is on understanding and applying the factorial rule as part of learning outcome 4.4. The factorial rule is a special case of the multiplication counting rule, crucial for accurately counting outcomes in probability. The video explains the concept of factorials, demonstrates their application through real-world examples like arranging dinner guests, and delves into classic combinatorics problems such as the traveling salesman problem. By the end of the video, viewers will grasp how to use factorials for various counting problems, laying the groundwork for future lessons on permutations and combinations.
Takeaways
- 📚 The lesson is focused on learning outcome number two and lesson 4.4, which involves understanding and applying the factorial rule.
- 🔢 The factorial rule is a special case of the multiplication counting rule and is part of five methods for counting discussed in the chapter.
- 🎲 The importance of these counting rules lies in their application to accurately count the number of outcomes in probability scenarios.
- 📉 Factorial is denoted by an exclamation point and represents the product of decreasing whole numbers, e.g., 5! = 5 × 4 × 3 × 2 × 1.
- ⚠️ The notation for n factorial is n multiplied by each whole number less than itself down to 1, with 0! defined as 1 based on the gamma function.
- 🔄 The factorial rule states that the number of different arrangements of n different items, when all are selected, is n factorial, emphasizing that order matters.
- 🎉 An example given is arranging 12 guests at a dinner table, illustrating how 12! provides the total number of seating arrangements.
- 🗺️ The traveling salesman problem is used as a classic example to explain the factorial rule, calculating the number of itineraries to visit cities.
- 🤔 The probability of visiting cities in alphabetical order is calculated as one specific arrangement divided by the total number of possible arrangements.
- 🧮 The script provides a step-by-step explanation of how to calculate factorials and apply them to real-world counting problems, emphasizing the use of calculators for large numbers.
- 📈 The lesson is part of a series that will cover permutations with identical and distinct objects, as well as combinations with distinct objects, expanding on the factorial rule.
Q & A
What are the learning outcomes for lesson 4.4 in the video?
-The learning outcomes for lesson 4.4 are to understand and apply the factorial rule, which is a special case of the multiplication counting rule, and to put it in context with other counting methods such as permutations and combinations.
Why is it important to accurately count the number of outcomes in probability?
-Accurate counting of outcomes is important in probability because it allows for the correct calculation of the likelihood of different events, which is essential for understanding and predicting the outcomes of various scenarios.
What does the factorial symbol (!) represent in mathematics?
-The factorial symbol (!) represents the product of decreasing whole numbers starting from the number to the left of the symbol down to 1.
How is n factorial mathematically represented for a positive integer n?
-n factorial is represented as n! and is calculated by multiplying n by each integer less than n down to 1, i.e., n! = n × (n-1) × (n-2) × ... × 3 × 2 × 1.
What is the definition of zero factorial, and why is it defined as such?
-Zero factorial is defined as 0! = 1. This definition is based on the gamma function in calculus, which extends the factorial function to non-integer values.
What is the factorial rule, and how is it applied in counting arrangements?
-The factorial rule states that the number of different arrangements of n different items, when all n of them are selected, is n factorial. It is applied by considering the order of arrangements, where the first item can be selected in n ways, the second in n-1 ways, and so on.
Can you provide an example of how the factorial rule is used in a real-world scenario?
-An example is the seating arrangement at a dinner party. If there are 12 guests and 12 seats with no constraints, the number of different seating arrangements is 12 factorial, calculated as 12!.
What is the traveling salesman problem, and how does the factorial rule apply to it?
-The traveling salesman problem is a classic combinatorics problem where one must find the shortest possible route to visit a given set of cities and return to the origin city. The factorial rule applies by calculating the number of different itineraries as n factorial, where n is the number of cities.
How many different travel itineraries are possible for a traveling salesman visiting five cities?
-There are 120 different travel itineraries possible for visiting five cities, calculated as 5 factorial (5!).
What is the probability of visiting five cities in alphabetical order if each city has a unique name?
-The probability of visiting five cities in alphabetical order is 1 out of 120, since there is only one way to list them in alphabetical order out of the 120 possible itineraries.
What is the significance of the factorial rule in combinatorics and probability?
-The factorial rule is significant in combinatorics and probability as it provides a method to calculate the total number of arrangements or permutations for a given set of items, which is crucial for determining probabilities and analyzing various counting problems.
Outlines
📚 Introduction to Factorial Rule in Counting Methods
This paragraph sets the stage for learning outcome number two, lesson 4.4, which focuses on the factorial rule in counting methods. The speaker emphasizes the importance of accurately counting outcomes in probability and introduces the factorial rule as a special case of the multiplication counting rule. The factorial is defined as the product of decreasing whole numbers, denoted by an exclamation point, with zero factorial being equal to one based on the gamma function. The speaker illustrates the concept with the example of arranging guests at a dinner party, explaining how the factorial rule can be used to calculate the number of possible seating arrangements.
🗺 The Factorial Rule and Traveling Salesman Problem
The second paragraph delves into the factorial rule's application, using the classic traveling salesman problem as an example. It explains how the factorial rule is a special case of the multiplication counting rule and applies it to calculate the number of possible itineraries for visiting five cities. The paragraph also addresses the probability of visiting cities in alphabetical order, given that all cities have unique names, and demonstrates how to calculate this probability by dividing the one way to list them alphabetically by the total number of itineraries. This example showcases the practical use of the factorial rule in combinatorics and counting problems.
Mindmap
Keywords
💡Factorial Rule
💡Multiplication Counting Rule
💡Permutations
💡Combinations
💡Gamma Function
💡Probability
💡Traveling Salesman Problem
💡Sample Space
💡Arrangement
💡Distinct Objects
Highlights
The video discusses Learning Outcome Number 2 and Lesson 4.4, focusing on understanding and applying the factorial rule.
Learning Outcome 4.4 aims to teach five counting methods, including the factorial rule, which is a special case of the multiplication counting rule.
The importance of accurate counting in probability is emphasized, especially for counting outcomes associated with events or the sample space.
Factorial is defined as the product of decreasing whole numbers, denoted by an exclamation point (e.g., 5 factorial is 5x4x3x2x1).
The notation for n factorial is n multiplied by (n-1) down to 1, with zero factorial defined as one based on the gamma function.
The factorial rule states that the number of arrangements of n different items, when all are selected, is n factorial.
Order matters in arrangements, exemplified by different seating arrangements at a dinner party with 12 guests.
Calculating 12 factorial results in 479 million 1,600 possible seating arrangements without constraints.
The factorial rule is a special case of the multiplication rule, where the first item has n possibilities and subsequent items have fewer.
The traveling salesman problem is introduced as a classic example of combinatorics and counting.
For a traveling salesman visiting five cities, there are 120 different itineraries possible, calculated by 5 factorial.
The probability of visiting cities in alphabetical order is one out of the total number of itineraries if all city names are unique.
The video provides a step-by-step explanation of how to apply the factorial rule to practical problems like the traveling salesman problem.
The video concludes with a summary of the factorial rule and its application in combinatorics and probability.
The video is part of a series on counting methods, with upcoming lessons on permutations, combinations, and their variations.
The factorial rule is applicable to real-world counting problems and is one of the fundamental concepts in combinatorics.
The video emphasizes the importance of understanding factorials for accurately counting outcomes in various scenarios.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: