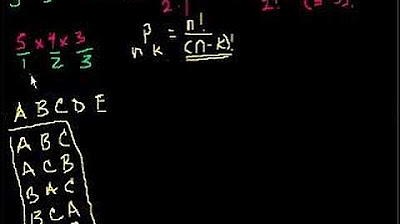Statistics Lecture 4.7: Fundamental Counting Rule, Permutations and Combinations
TLDRThe video script explores the fundamental counting rule, permutations, and combinations. It begins with a basic introduction to counting outcomes using a coin and die example. The fundamental counting rule is explained, followed by practical applications such as calculating possible PIN numbers and security codes. The script then delves into permutations, emphasizing the importance of unique arrangements, and introduces factorial notation. Examples include arranging fruits and selecting a committee. Finally, combinations are discussed, highlighting scenarios where order doesn't matter, such as choosing rides at a theme park, and using calculator functions to simplify these calculations.
Takeaways
- 🪙 The session covers counting methods and the fundamental counting rule.
- 🎲 The fundamental counting rule states that if one event can occur in 'm' ways and another can occur in 'n' ways, then together they can occur in 'm x n' ways.
- 🔄 Using a coin and a die, the rule demonstrates how to calculate the total number of outcomes.
- 💡 Examples include permutations and combinations to illustrate the rule.
- 🔢 Permutations involve arranging distinct items, where order matters, calculated as 'n!'.
- 📝 Combinations involve selecting items where order doesn't matter, calculated using 'nCr'.
- 🔐 An example problem explains calculating the number of possible PIN codes given certain constraints.
- 🍎 Using fruits, the session explains how to calculate arrangements when items are not unique.
- 📚 The concept of factorials is introduced to simplify calculations involving multiple items.
- 🔍 Practical examples include selecting committee members and calculating different ride combinations.
Q & A
What is the fundamental counting rule?
-The fundamental counting rule states that if you have one event that can occur in m ways and another event that can occur in n ways, then together they can occur in m * n ways.
How does the fundamental counting rule apply to flipping a coin and rolling a die?
-When flipping a coin and rolling a die, you get 2 outcomes for the coin (heads or tails) and 6 outcomes for the die (1-6). According to the fundamental counting rule, the total number of outcomes is 2 * 6 = 12.
What is a permutation?
-A permutation is an arrangement of items where the order matters. For example, arranging 5 unique fruits in different orders.
How do you calculate the number of permutations for a set of items?
-The number of permutations for a set of n items is calculated as n factorial (n!). For example, 5! = 5 * 4 * 3 * 2 * 1 = 120.
What is a combination?
-A combination is a selection of items where the order does not matter. For example, selecting 5 rides out of 25 at an amusement park.
How do you calculate the number of combinations for a set of items?
-The number of combinations for selecting r items from n items is calculated using the formula C(n, r) = n! / [r! * (n - r)!].
How does the permutation formula differ from the combination formula?
-The permutation formula is P(n, r) = n! / (n - r)!, which accounts for the order of selection. The combination formula is C(n, r) = n! / [r! * (n - r)!], which does not account for the order of selection.
What happens if the items to be arranged are not unique?
-If the items are not unique, the number of arrangements is reduced by dividing by the factorial of the number of each set of identical items. For example, if you have 3 apples, 2 oranges, and 5 bananas, the formula is 10! / (3! * 2! * 5!).
How do you use a calculator to compute permutations and combinations?
-To compute permutations and combinations on a calculator, use the functions nPr for permutations and nCr for combinations, usually found under the math or probability menu.
What is the importance of understanding permutations and combinations in probability?
-Understanding permutations and combinations is crucial in probability to calculate the likelihood of different outcomes and to understand the various ways items or events can be arranged or selected.
Outlines
🔢 Fundamental Counting Rule Introduction
The speaker introduces the fundamental counting rule using a coin and die example. They explain how to calculate the number of outcomes by multiplying the number of possible results for each event, emphasizing the concept with a step-by-step breakdown.
🔢 Extended Example: PIN Numbers
An example of calculating the number of possible PIN numbers is given, illustrating the fundamental counting rule. The speaker explains the restriction that the first digit cannot be zero and shows how to calculate the total combinations for a four-digit PIN.
🔢 Probability and Combinations
The speaker discusses the probability of guessing a PIN correctly on the first try and how the probability increases with more attempts. They use this to further explain the application of the fundamental counting rule in calculating the total number of possible combinations.
🍏 Arrangements of Fruits: Introduction to Permutations
Using the example of arranging five different fruits, the speaker explains how to calculate the number of possible arrangements (permutations). They emphasize how the choices decrease as each fruit is placed, leading to the calculation of permutations.
🍌 More Examples with Fruits
The speaker continues with the fruit arrangement example, showing how the number of choices decreases with each subsequent selection. They explain the concept of factorial and introduce the notation for calculating permutations.
🎢 Disney Rides Example
The concept of permutations is further illustrated using the example of visiting seven distinct rides at Disneyland. The speaker calculates the total number of possible orderings of the rides using the factorial notation.
🔢 Calculating Permutations with a Calculator
The speaker demonstrates how to use a calculator to compute permutations. They show how to input numbers and use the factorial function to quickly find the number of possible arrangements for large numbers.
🔢 Introduction to Combinations
The speaker introduces combinations, explaining how they differ from permutations. They provide an example where the order of selection does not matter, highlighting the concept with a governor visiting counties in California.
🔢 More on Combinations
An example of selecting counties to visit as a governor is discussed in detail. The speaker explains how to calculate the number of ways to select a subset of items (combinations) from a larger set when order does not matter.
🔢 Rules for Combinations
The speaker lays out the rules for calculating combinations, emphasizing that the items must be unique, and the order does not matter. They introduce the formula for combinations and show how to apply it to real-world examples.
🔢 Calculating Combinations with a Calculator
The speaker demonstrates how to use a calculator to compute combinations. They explain how to input values and use the NCR function to quickly determine the number of possible combinations.
🔢 Example with Repeated Items
An example involving a fictional election is provided to illustrate how combinations are used when selecting a group of people. The speaker explains the importance of unique items and how to handle repeated items in calculations.
🔢 Revisiting Permutations and Combinations
The speaker revisits the differences between permutations and combinations. They explain when to use each method and provide additional examples to reinforce the concepts.
🍏 Example with Non-Unique Items
A detailed example is given involving non-unique items (fruits). The speaker explains how to account for repeated items by dividing out the number of identical items using factorials.
🍎 Calculating Arrangements with Non-Unique Items
The speaker continues the example with fruits, showing how to calculate the number of unique arrangements when some items are identical. They explain how to simplify the calculation using factorials.
📝 Example with Letters: Statistics
Using the word 'statistics,' the speaker demonstrates how to calculate the number of unique arrangements of letters. They apply the concept of non-unique items and show how to simplify the calculation.
👨👩👧👦 Example with a Family
An example is provided involving planning a family with seven girls and five boys. The speaker explains how to calculate the number of unique arrangements using combinations and factorials.
🔢 Introduction to Combinations
The speaker introduces combinations, explaining the concept and how it differs from permutations. They provide examples to illustrate when to use combinations and how to calculate them.
🎢 Example with Rides at Magic Mountain
The speaker provides an example involving selecting rides at Magic Mountain. They explain how to calculate the number of ways to select a subset of rides using combinations when the order does not matter.
🔢 Summary and Final Example
The speaker concludes the session by summarizing the key points about permutations and combinations. They provide a final example to reinforce the concepts and demonstrate how to use a calculator for these calculations.
Mindmap
Keywords
💡Fundamental Counting Rule
💡Permutation
💡Combination
💡Factorial
💡Distinct Items
💡Non-distinct Items
💡Outcome
💡Event
💡Probability
💡PIN Number
Highlights
Introduction to the fundamental counting rule for determining the number of outcomes in sequential events.
Explanation of the fundamental counting rule with a coin and die example, demonstrating how to calculate total outcomes.
Application of the fundamental counting rule to calculate possible PIN numbers, considering restrictions on the first digit.
Extension of the fundamental counting rule to more complex scenarios, such as larger sequences of events.
Real-life example involving forgotten PIN numbers to illustrate the application of the fundamental counting rule.
Discussion on the security of PIN numbers based on the number of possible combinations.
Example of arranging fruits to demonstrate the concept of permutations and the factorial calculation.
Introduction to the concept of permutations and how they differ from combinations.
Explanation of the permutation formula and its application to real-life scenarios, such as election campaigning.
Step-by-step guide on calculating permutations using a calculator, including factorial operations.
Discussion on non-unique items and how they affect the total number of arrangements, with a fruit example.
Explanation of how to handle non-distinct items in permutations by dividing by the factorial of the number of non-unique items.
Introduction to combinations, where the order of selection does not matter.
Comparison between permutations and combinations, emphasizing when to use each based on the importance of order.
Formula for calculating combinations and a guide on using calculators to find combination values.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: