Simple Harmonic Motion

Bozeman Science

29 Aug 201408:05

EducationalLearning

32 Likes 10 Comments

TLDRIn this AP Physics essentials video, Mr. Andersen explores simple harmonic motion, using a child on a swing as an analogy. He explains the restoring forces behind the motion and discusses two key examples: the mass-spring oscillator and the pendulum. The video delves into how the period of these systems is affected by mass, spring stiffness, pendulum length, and gravitational field strength. Through experiments and simulations, Mr. Andersen illustrates how changes in these properties influence the period and the motion's characteristics, providing insights into predicting and understanding harmonic motion.

Takeaways

📈 Simple harmonic motion is characterized by an object moving back and forth with a restoring force acting towards equilibrium.
🏋️ Examples of simple harmonic motion include a child on a swing and a mass-spring oscillator bouncing up and down, or a pendulum swinging.
📐 The period of harmonic motion, measured in seconds, is the time taken for one complete cycle of the motion.
🔨 To increase the period of a mass-spring oscillator, one can increase the mass of the object or decrease the spring's stiffness.
🔩 Conversely, to decrease the period of a mass-spring oscillator, make the spring stiffer or decrease the mass.
⏳ For a pendulum, the period can be increased by lengthening the pendulum or by decreasing the gravitational field strength.
🌍 The mass of the pendulum does not affect its period, unlike in a mass-spring system.
📉 Decreasing the length of a pendulum results in a shorter period, speeding up the motion.
🌙 Changing the gravitational field strength affects the period of a pendulum; stronger fields decrease the period, while weaker fields increase it.
🔢 The period of a spring (T_spring) is influenced by the mass (m) and the spring constant (k), with the formula T_spring = 2π√(m/k).
🌐 The period of a pendulum (T_pendulum) is influenced by its length (L) and the gravitational field strength (g), with the formula T_pendulum = 2π√(L/g).

Q & A

What is simple harmonic motion?
-Simple harmonic motion is a type of periodic motion where an object moves back and forth along a single axis under the influence of a restoring force that always points towards the equilibrium position.
What are two examples of simple harmonic motion discussed in the video?
-The two examples discussed are the mass-spring oscillator and the pendulum.
How does the period of a mass-spring oscillator change with mass?
-The period of a mass-spring oscillator increases as the mass hanging from the spring increases.
How can the period of a mass-spring oscillator be decreased?
-The period can be decreased by making the spring stiffer, which means increasing the spring constant.
What factors affect the period of a pendulum?
-The period of a pendulum is affected by its length and the strength of the gravitational field in which it is swinging.
How does the mass of a pendulum influence its period?
-The mass of a pendulum does not affect its period when swinging under normal gravitational conditions.
What happens to the period of a pendulum when the gravitational field strength is increased?
-When the gravitational field strength is increased, the period of the pendulum decreases, causing it to swing faster.
What is the relationship between the period of a spring and its mass and spring constant?
-The period of a spring is directly proportional to the square root of the mass and inversely proportional to the square root of the spring constant.
How does changing the length of a pendulum affect its period?
-As the length of a pendulum increases, its period also increases, meaning it takes more time to complete one full oscillation.
What can be observed about the position, velocity, and acceleration of an object in simple harmonic motion at its maximum displacement?
-At maximum displacement, the object's position is at its extreme, velocity is zero, and acceleration is at its maximum towards the equilibrium position.
At the equilibrium position during simple harmonic motion, what are the velocity and acceleration of the object?
-At the equilibrium position, the object's velocity is at its maximum, and there is no acceleration since it is not being pulled towards or away from the equilibrium.

Outlines

00:00

📏 Simple Harmonic Motion and Its Characteristics

This paragraph introduces the concept of simple harmonic motion (SHM), using the analogy of pushing an object in equilibrium that results in a restoring force bringing it back to equilibrium. Two examples are discussed: a mass-spring oscillator and a pendulum. The paragraph emphasizes the importance of the period of SHM, which is measured in seconds and represents the time taken for a complete oscillation. It explains how the period can be altered by changing the mass in a mass-spring system or the spring's stiffness. For a pendulum, the period is affected by the length of the pendulum and the strength of the gravitational field, with mass having no impact on the period. The paragraph also touches on the ability to predict an object's position, velocity, and acceleration at any given time during SHM.

05:03

🔧 Experimenting with Mass-Spring Oscillators and Pendulums

This paragraph delves into experiments with mass-spring oscillators and pendulums using PHET simulations to illustrate how different properties affect the period of SHM. It demonstrates that increasing mass in a mass-spring system results in a longer period, while increasing the spring's stiffness (making it stiffer) leads to a shorter period. For pendulums, it shows that decreasing the length results in a faster period, whereas increasing the gravitational field strength slows down the pendulum's swing. The paragraph concludes with a qualitative summary of the findings: increasing mass extends the period for a mass-spring oscillator, increasing stiffness shortens it; for pendulums, increasing length extends the period, and increasing gravitational field strength shortens it.

Mindmap

Keywords

💡Simple Harmonic Motion

Simple Harmonic Motion (SHM) is a type of periodic motion where an object moves back and forth along a straight line under the influence of a restoring force that is proportional to the displacement from its equilibrium position. In the context of the video, SHM is exemplified by a child on a swing and a mass-spring oscillator. The restoring force is what causes the object to return to its equilibrium state, and this motion is characterized by its periodic nature, with the period being a key property.

💡Restoring Force

A restoring force is a force that acts to return a body to its equilibrium position. In the context of simple harmonic motion, this force is what drives the periodic nature of the motion. The restoring force is directly proportional to the displacement from the equilibrium position and acts in the opposite direction. For instance, in a mass-spring system, the spring's force is the restoring force that pulls the mass back towards its equilibrium position.

💡Equilibrium

Equilibrium in physics refers to a state where all forces acting on an object are balanced, resulting in no net force and thus no acceleration. In the context of the video, the equilibrium position is the central position around which the object (like a mass-spring system or a pendulum) oscillates. The restoring forces act to return the object to this equilibrium state whenever it is displaced from it.

💡Period

The period of a motion is the time taken for one complete cycle of the motion. In the context of simple harmonic motion, the period is a critical characteristic that describes how long it takes for the object to complete one full oscillation from its initial position and back. The period is measured in seconds and is influenced by factors such as the mass of the object and the stiffness of the spring in a mass-spring system, or the length of the pendulum and the gravitational field strength for a pendulum.

💡Mass-Spring Oscillator

A mass-spring oscillator is a mechanical system consisting of a mass attached to a spring. The mass oscillates back and forth due to the restoring force of the spring, which is an example of simple harmonic motion. The motion of the mass is influenced by the mass itself and the spring's stiffness, with the period of oscillation depending on these two properties.

💡Pendulum

A pendulum is a weight suspended from a pivot so that it can swing freely back and forth. The motion of a pendulum is a form of simple harmonic motion when the swings are of small amplitude. The period of a pendulum is not affected by the mass of the pendulum but depends on the length of the pendulum and the gravitational field strength.

💡Acceleration

In physics, acceleration is the rate of change of velocity of an object with respect to time. It is a vector quantity that describes how quickly the velocity of an object changes. In the context of simple harmonic motion, acceleration is zero at the equilibrium position and maximum at the extreme positions of the motion. The direction of the acceleration is always towards the equilibrium position, acting as a restoring force.

💡Displacement

Displacement in the context of simple harmonic motion refers to the change in position of the oscillating object from its equilibrium position. It is a vector quantity that points from the equilibrium position to the current position of the object. The magnitude of displacement is maximum at the ends of the oscillation and zero at the equilibrium position.

💡Stiffness

Stiffness, in the context of a spring, refers to the spring's resistance to being compressed or stretched. It is quantified by the spring constant (k), which is the force required to cause a unit displacement. A stiffer spring has a higher spring constant and will resist deformation more than a less stiff spring. In simple harmonic motion, the stiffness of the spring affects the period of the oscillation; a stiffer spring results in a shorter period.

💡Gravitational Field Strength

Gravitational field strength, often denoted by g, is a measure of the intensity of the gravitational force at a point in space. It is the acceleration due to gravity at that point. In the context of a pendulum's motion, the gravitational field strength affects the period of the pendulum's oscillation; a stronger gravitational field results in a shorter period.

💡Damping

Damping refers to the reduction of amplitude or energy in a vibrating system. In the context of simple harmonic motion, damping forces are those that resist the motion and cause the oscillation to gradually decrease in amplitude over time. These forces are typically proportional to the velocity of the oscillating object and act in the opposite direction to the motion.

Highlights

Simple harmonic motion is characterized by a restoring force that returns an object towards equilibrium.

An example of simple harmonic motion is pushing a child on a swing.

Two examples in AP Physics are the mass-spring oscillator and the pendulum.

The period of harmonic motion is measured in seconds and represents the time for one complete oscillation.

Increasing the mass of a mass-spring oscillator increases its period.

Decreasing the stiffness of a spring in a mass-spring oscillator decreases its period.

For a pendulum, increasing its length increases the period.

The mass of a pendulum does not affect its period.

Increasing the gravitational field strength decreases the period of a pendulum.

In a mass-spring oscillator, the position, velocity, and acceleration of the object can be identified at any time.

At the equilibrium position, the velocity is at its maximum and acceleration is zero.

At the maximum displacement, the velocity is zero and the acceleration is at its maximum.

A PHET simulation can be used to experiment with the effects of mass and stiffness on a mass-spring oscillator's period.

A pendulum's period can be qualitatively measured using a photo gate timer.

Theoretical equations can be used to predict the quantitative effects of mass, stiffness, length, and gravitational field strength on the period of harmonic motion.

Understanding the properties affecting harmonic motion is crucial for predicting and analyzing physical systems.

Transcripts

Browse More Related Video

Simple Harmonic Motion - Physics 101 / AP Physics 1 Review with Dianna Cowern

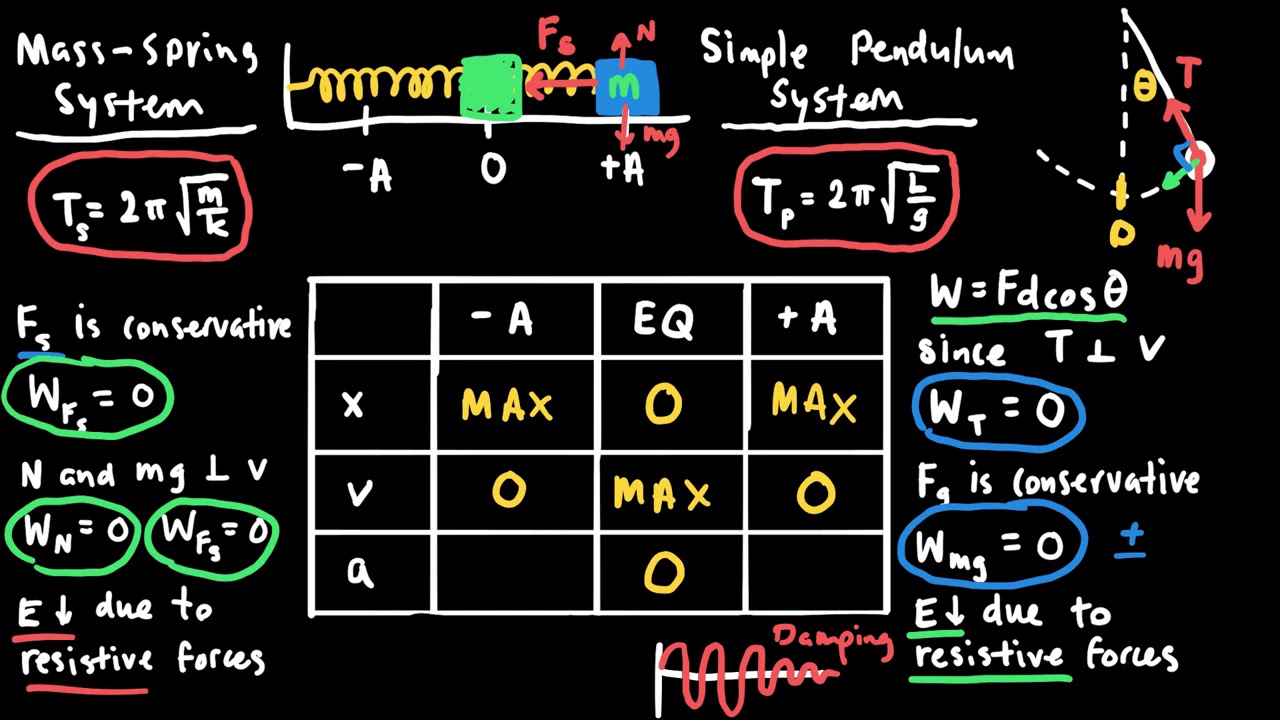
AP Physics 1 Simple Harmonic Motion, Mechanical Waves, and Sound Review

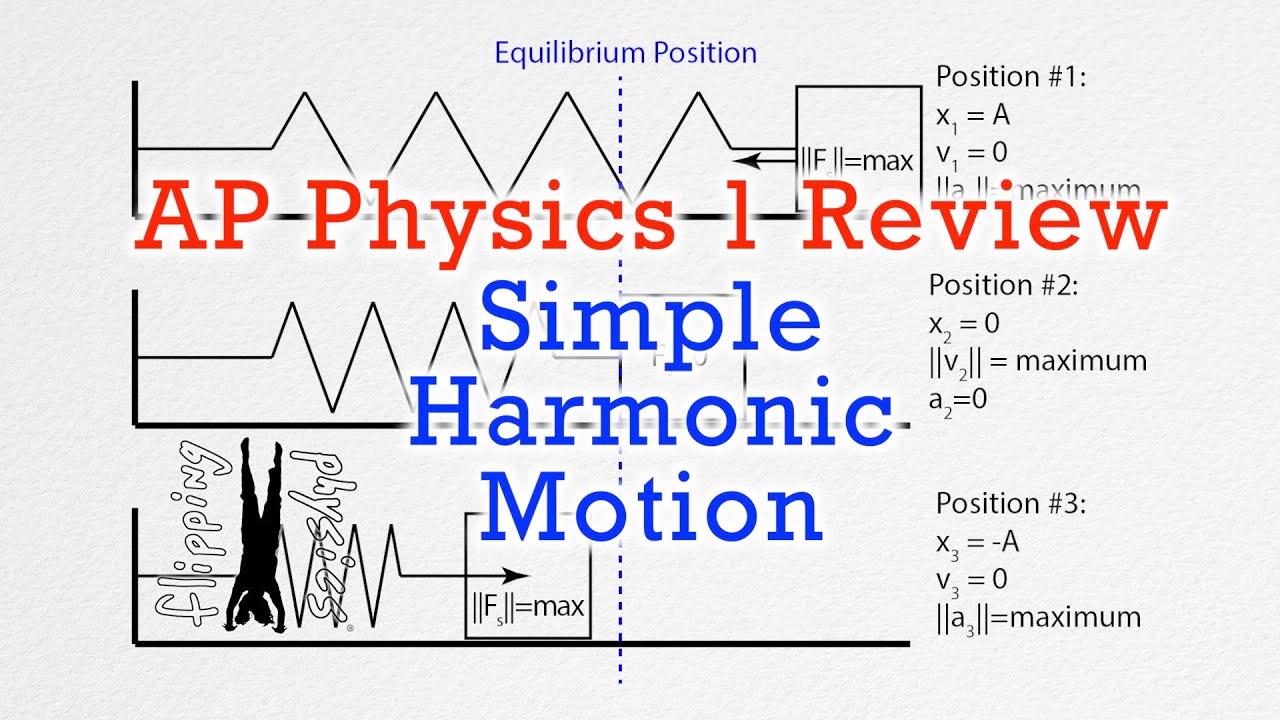
AP Physics 1: Simple Harmonic Motion Review

Pendulums | Oscillations and mechanical waves | Physics | Khan Academy

8.01x - Lect 10 - Hooke's Law, Springs, Pendulums, Simple Harmonic Motion

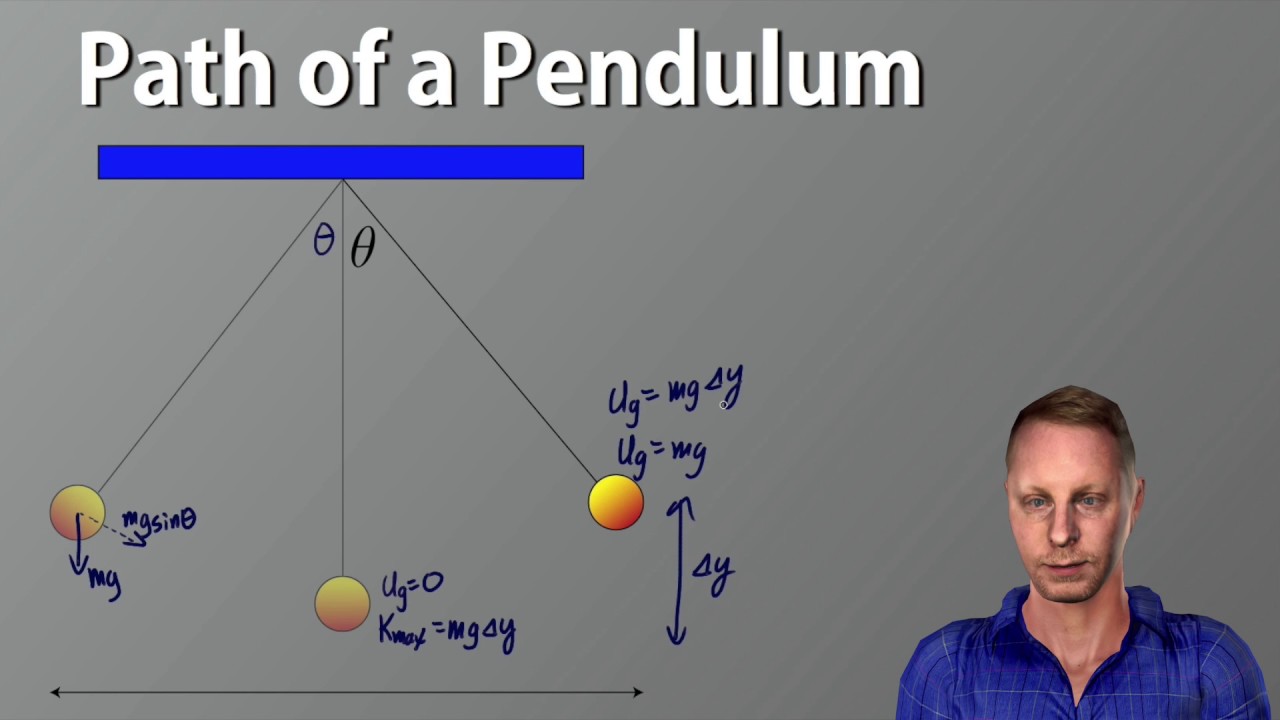
AP Physics 1 - Pendulums

Simple Harmonic Motion

Takeaways

Q & A

What is simple harmonic motion?

What are two examples of simple harmonic motion discussed in the video?

How does the period of a mass-spring oscillator change with mass?

How can the period of a mass-spring oscillator be decreased?

What factors affect the period of a pendulum?

How does the mass of a pendulum influence its period?

What happens to the period of a pendulum when the gravitational field strength is increased?

What is the relationship between the period of a spring and its mass and spring constant?

How does changing the length of a pendulum affect its period?

What can be observed about the position, velocity, and acceleration of an object in simple harmonic motion at its maximum displacement?

At the equilibrium position during simple harmonic motion, what are the velocity and acceleration of the object?