Linear Approximations | Using Tangent Lines to Approximate Functions
TLDRThe video script discusses the concept of derivatives and their practical application in approximating functions. It uses the sine function and the square root function as examples to illustrate how tangent lines, derived from the derivative of a function, can closely approximate the original function near a given point. The presenter demonstrates how by zooming in on a graph, the tangent line and the function itself can appear almost identical, indicating a high degree of approximation accuracy. The script also explores the process of linear approximation, showing how to use the tangent line at a known point to estimate the value of a function at a nearby point. This is demonstrated by approximating the square root of 1.5 using the tangent line at the point where X equals 1. The presenter concludes by emphasizing the linear approximation formula, which is essentially the equation of the tangent line at a specific point, evaluated at another point, as a useful tool for estimating function values.
Takeaways
- 📌 The derivative of a function gives the slope of the tangent line, which is a useful tool for approximating the function near a point.
- 📈 The tangent line to a function at a specific point is a good approximation of the function near that point but may not be accurate far away.
- 🤔 The concept of zooming in on a graph can illustrate how closely the tangent line matches the function, especially when the window is narrowed.
- 🔍 By zooming in enough, the tangent line and the original function can appear almost interchangeable, showing the power of linear approximations.
- 🧮 Linear approximation is a method to estimate the value of a function at a point near another known point using the tangent line at the known point.
- 📐 The point-slope form of a line is used to express the equation of the tangent line, which is crucial for linear approximations.
- 🔢 The derivative of the square root of x (x^(1/2)) is found by applying the power rule, resulting in (1/2)x^(-1/2).
- 📉 For the function √x, the tangent line at x=1 is used to approximate the value of √1.5 by evaluating the tangent line at x=1.5.
- 💡 The approximation of √1.5 using the tangent line at x=1 results in a value close to the actual square root, demonstrating the effectiveness of linear approximation.
- 📊 The general linear approximation formula involves the function value at a known point, the derivative at that point, and the distance between the known point and the point of interest.
- ✅ The linear approximation formula is essentially the equation of the tangent line at a known point, evaluated at the point of interest, providing an estimate for the function's value.
Q & A
What is the main purpose of a derivative in the context of the script?
-The main purpose of a derivative is to give us the slope of the tangent line, which is a good approximation of the function near a specific point.
Why does the tangent line provide a good approximation of the function near a certain point?
-The tangent line is a good approximation because it has the same slope as the function at that point, making it closely follow the function's curve near that point.
How does the distance from the point of tangency affect the approximation of the function by the tangent line?
-The further away from the point of tangency, the less accurate the approximation becomes, as the tangent line was derived based on the slope at a single point.
What is the process of zooming in on a graph to observe the approximation of the tangent line to the function?
-Zooming in on a graph allows us to narrow the window of observation, making it easier to see how closely the tangent line approximates the function within a smaller range.
What is the significance of knowing the square root of 1 when discussing the tangent line approximation of the square root function?
-Knowing the square root of 1 is significant because it provides a known point on the function where the tangent line can be accurately calculated and used as a reference for further approximations.
How does the concept of linear approximation relate to the tangent line at a point?
-Linear approximation uses the tangent line at a point to estimate the value of a function at a nearby point. It involves using the function value at a known point, the slope of the tangent line at that point, and the distance between the known point and the point of interest.
What is the general formula for a line in the context of the script?
-The general formula for a line is Y - Y_nought = M(X - X_nought), where Y and X are the variables, Y_nought and X_nought are the coordinates of a known point on the line, and M is the slope of the line.
How is the slope of the tangent line related to the derivative of the function?
-The slope of the tangent line is given by the derivative of the function at the point of tangency. The derivative represents the rate of change of the function, which is the slope of the tangent line at that point.
What is the power rule used for in the script?
-The power rule is used to find the derivative of the square root of x, which is expressed as x to the power of 1/2. It states that the derivative of x^n is n*x^(n-1).
How does the script use the point-slope form to find the equation of the tangent line?
-The script uses the point-slope form by knowing a point on the tangent line (X_nought, Y_nought) and the slope (M) at that point, derived from the derivative of the function. It then plugs these into the point-slope formula to find the equation of the tangent line.
What is the linear approximation formula used to estimate the square root of 1.5 in the script?
-The linear approximation formula used is L(X) = f(a) + f'(a) * (X - a), where f(a) is the function value at the approximating point, f'(a) is the derivative at that point, and X is the point near a that we want to approximate.
Outlines
📈 Understanding Tangent Lines as Approximations
This paragraph discusses the concept of derivatives and their practical use in approximating the behavior of functions near a given point. The author uses the graph of the sine function to illustrate how the tangent line closely matches the function near the point where the tangent line is drawn. The importance of the tangent line as a local approximation is emphasized, and the concept is further explored through the example of the square root function. The tangent line's role in approximating values of functions, such as the square root of 1.5, is highlighted, and the process of using the tangent line at one point to estimate the function's value at another point is explained.
🧮 Deriving the Tangent Line Formula for √x
The second paragraph delves into the mathematical process of finding the tangent line for the square root function at a specific point, in this case, x=1. The author explains the general formula for a line, known as the point-slope form, and how it can be adapted to find the tangent line. The derivative of the square root of x, which is 1/(2√x), is calculated to determine the slope of the tangent line. By substituting x=1 into the derivative, the slope of the tangent line at that point is found to be 1/2. The author then uses this slope to write the equation of the tangent line at x=1 and evaluates it at x=1.5 to approximate the square root of 1.5. The approximation is compared with the actual value obtained from a calculator, showing that the tangent line provides a close estimate.
Mindmap
Keywords
💡Derivative
💡Tangent Line
💡Slope
💡Linear Approximation
💡Square Root
💡Point-Slope Formula
💡Power Rule
💡Error
💡Zooming In
💡Graphical Picture
💡Slope-Intercept Form
Highlights
Derivatives provide the slope of the tangent line, which is a good approximation of the function near a point.
The tangent line is a very close approximation of the sine function near x=0, but not far away from that point.
Zooming in on the graph makes the tangent line and the original function appear almost interchangeable for the sine function.
The square root function and its tangent line at x=1 are very close, and become indistinguishable when zoomed in.
The square root of 1.5 can be approximated by evaluating the tangent line of the square root function at x=1 and then at x=1.5.
The tangent line provides a good approximation of the square root function at points close to the point of tangency.
The tangent line at x=1 can be used to approximate the value of the square root function at x=1.5 with a small error.
The square root of 1.5 is approximately equal to the tangent line evaluated at x=1.5, which is 1.25.
The actual square root of 1.5 calculated using a calculator is 1.22, which is close to the approximation of 1.25.
The linear approximation formula states that f(x) near a point can be approximated by f(a) + f'(a) * (x - a).
The linear approximation formula is essentially the equation of the tangent line at point a, evaluated at point x.
The tangent line provides a simple and effective way to approximate functions near a given point.
The approximation error decreases as the point x gets closer to the point of tangency.
The process of linear approximation involves finding the function value and slope at an approximating point, and using them to estimate the function value at a nearby point.
Linear approximation is a useful technique for approximating functions when exact values are difficult to compute.
The tangent line can be used to approximate the value of a function at a point where the function is not easily computable.
The linear approximation formula is derived from the point-slope form of a line, with the function value, slope, and point of tangency as inputs.
Transcripts
Browse More Related Video

Linear Approximation

Calculus AB/BC – 4.6 Approximating Values of a Function Using Local Linearity and Linearization
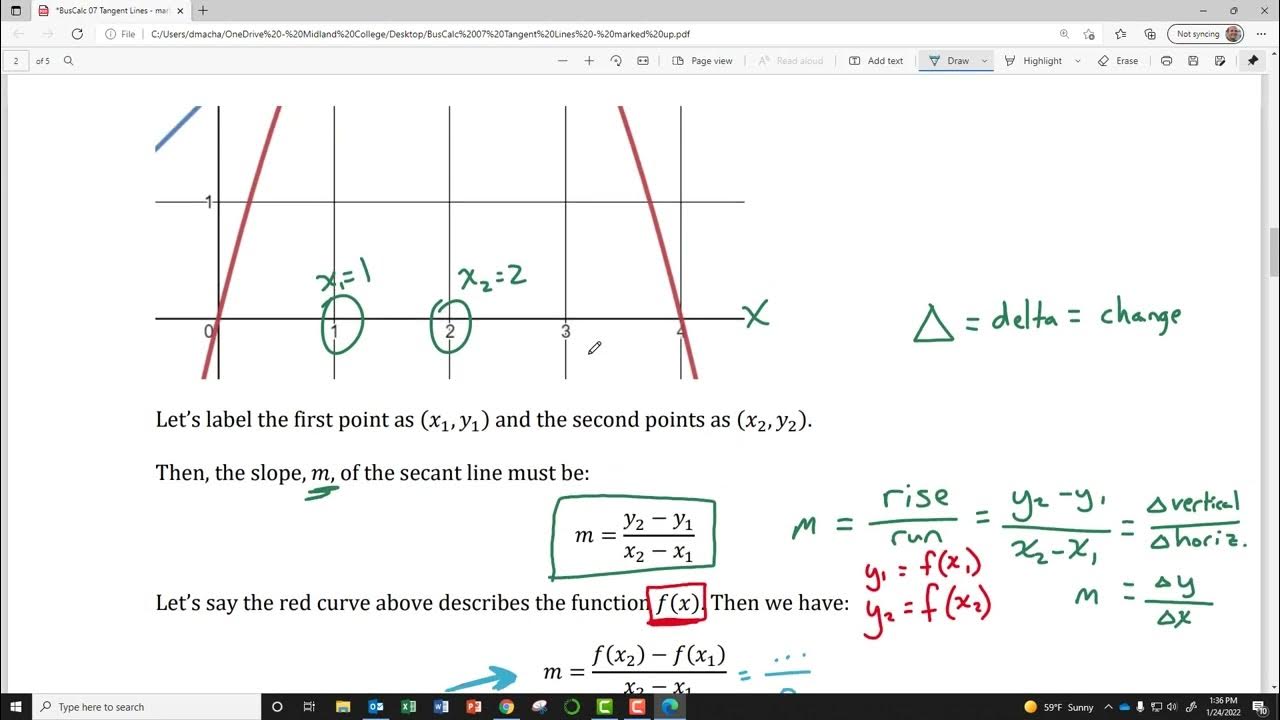
BusCalc 07 Tangent Lines

AP Calculus AB: Lesson 2.6 Tangent Line Approximations

Definition of the Derivative | Part I

Finding The Linearization of a Function Using Tangent Line Approximations
5.0 / 5 (0 votes)
Thanks for rating: