Continuity and Differentiability EXPLAINED with Examples
TLDRIn this educational video, Mark from Ace Tutors explains the concepts of continuity and differentiability with clear examples. He outlines the three requirements for a function to be continuous at a point and emphasizes the importance of the limit's existence and equality to the function's value at that point. Mark also discusses the conditions for a function to be continuous on an interval, highlighting the 'no pencil pick-up' rule. He then moves on to differentiability, stating that a function's derivative must exist at every point within an interval for it to be differentiable. Examples of non-differentiable functions due to sharp points or slope changes are provided, and a few rules of thumb are shared for remembering these mathematical properties.
Takeaways
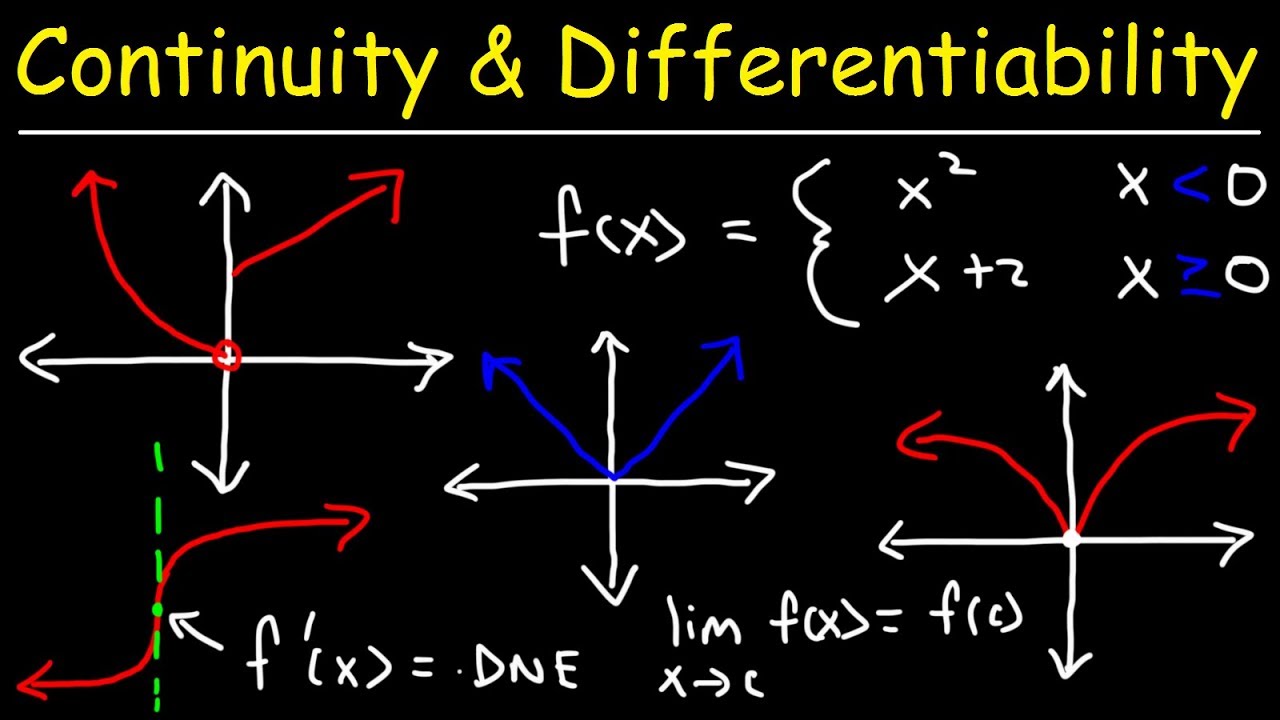
- 📌 A function is continuous at a point if it meets three criteria: the function is defined at that point, the limit exists as x approaches that point, and the limit equals the function's value at that point.
- 📈 Continuity on an interval means the function is continuous at every point within that interval, or you can draw the function without lifting your pencil.
- 🚫 Discontinuities can occur due to holes where the function is not defined, unequal left and right limits, or the limit not equaling the function's value at a point.
- 🔍 Differentiability at a point requires the existence of the function's derivative at that point, indicating a definite slope value.
- 📊 For a function to be differentiable on an interval, it must be differentiable at every point within that interval, meaning the derivative exists for every point.
- 🚧 Examples of non-differentiable functions include those with corners or cusps where the slope jumps from negative to positive, indicating an undefined slope at that point.
- 📚 The script provides visual examples to illustrate the concepts of continuity and differentiability, helping to solidify understanding.
- 👍 The video encourages viewer engagement by asking for likes and subscriptions to support the creation of more educational content.
- 📉 A function with a hole or a sharp point is not continuous or differentiable because it breaks the criteria for having a defined limit or derivative.
- 📝 The video script is designed to be educational, providing clear explanations and examples for the mathematical concepts of continuity and differentiability.
- 🎓 The presenter, Mark from Ace Tutors, aims to make complex mathematical topics accessible and understandable for the audience.
Q & A
What are the three requirements for a function to be continuous at a single point x equals a?
-For a function f(x) to be continuous at x=a, it must satisfy: 1) f(a) must be defined, meaning plugging in a yields a y-value. 2) The limit as x approaches a of f(x) must exist, which means the left and right limits are equal. 3) This limit must be equal to the value of f(a) when a is plugged into the function.
How can you determine if a function is continuous on an interval?
-A function is continuous on an interval if it is continuous at every point within that interval, meaning it satisfies the conditions for continuity without any breaks or gaps, allowing the function to be drawn without lifting the pencil.
What causes a function to be discontinuous?
-A function can be discontinuous due to reasons such as: 1) A hole or undefined value at a point (f(a) is not defined). 2) The left and right limits at a point are not equal, making the overall limit non-existent. 3) The overall limit does not equal the value of the function at that point, violating the third rule of continuity.
What is the condition for a function to be differentiable at a single point x equals a?
-A function is differentiable at x=a if the derivative of the function exists at that point, indicating a well-defined slope value for the function at x=a.
What does it mean for a function to be differentiable on an interval?
-A function is differentiable on an interval if it is differentiable at every point within that interval, meaning the derivative of the function exists for every point in the interval.
Why might a function not be differentiable at a certain point?
-A function might not be differentiable at a certain point if there is a sharp point or an instantaneous change in the function's slope, such as a corner or a cusp where the slope jumps from one value to another.
What is the relationship between the existence of a function's derivative and its differentiability?
-The existence of a function's derivative at a point is both a necessary and sufficient condition for the function to be differentiable at that point. If the derivative exists, the function is differentiable; if it does not, the function is not differentiable.
What is a simple way to remember the rule for a function to be continuous?
-A function is continuous if there are no breaks or gaps in its graph, and you can draw the function without picking up your pencil.
What is a simple way to remember the rule for a function to be differentiable?
-A function is differentiable if it is smooth, without any sharp points or instantaneous changes in the slope of the function.
What does the video suggest to do if you find the content helpful?
-If you find the video helpful, the video suggests to show support by liking and subscribing to encourage the creation of more such content.
What is the final message from the video creator to the viewers?
-The final message is an encouragement to pursue big dreams and not let a class or any obstacle get in the way of achieving them.
Outlines
📚 Continuity and Differentiability Basics
Mark from Ace Tutors introduces the concepts of continuity and differentiability with examples. Continuity at a point requires three conditions: the function must be defined at 'a', the limit as x approaches 'a' must exist from both sides, and this limit must equal the function's value at 'a'. He illustrates these points with a graph and explains how a function can be continuous on an interval if it meets these criteria at every point within that interval. Mark also discusses common reasons for discontinuity, such as holes in the function or limits from different sides not matching.
🔍 Differentiability Criteria and Examples
Continuing the tutorial, Mark explains differentiability at a point, which requires the existence of a function's derivative at that point. He uses a graph to show how a function's derivative can indicate differentiability. To be differentiable on an interval, the function must be differentiable at every point within that interval, meaning the derivative must exist everywhere. Mark provides examples of functions that are not differentiable due to sharp points or corners where the slope changes instantaneously, indicating the absence of a derivative at those points.
📘 Summary of Continuity and Differentiability Rules
Mark concludes the video with a summary of the rules for continuity and differentiability. For a function to be continuous, it must have no breaks or gaps, allowing it to be drawn without lifting the pencil. For differentiability, a function must be smooth, without any sharp points or instantaneous changes in slope. He invites feedback in the comments and encourages viewers to pursue their dreams despite academic challenges, ending the video on a motivational note.
Mindmap
Keywords
💡Continuity
💡Differentiability
💡Limit
💡Function
💡Derivative
💡Interval
💡Hole
💡Slope
💡Cusp
💡Smooth
💡Breaks or Gaps
Highlights
In order to figure out whether a function f(x) is continuous at a single point x = a, we need to satisfy three requirements: f(a) is defined, the limit as x approaches a of f(x) exists, and this limit equals f(a).
For a function to be continuous on an interval, it must be continuous at every point in the interval.
A function is not continuous if there is a hole at a point with no value defined for that x.
If the limit as x approaches a point from the left is different from the limit as x approaches it from the right, the function is discontinuous at that point.
A function can be discontinuous if the limit exists but does not equal the function's value at that point.
In order for a function to be differentiable at a single point x = a, its derivative must exist at that point.
A function is differentiable on an interval if its derivative exists at every point within that interval.
A function is not differentiable at a corner point where the slope instantaneously jumps from one value to another.
A function is not differentiable at a cusp where the slope instantaneously changes from negative to positive.
For continuity, there must be no breaks or gaps in the function; you must be able to draw the function without lifting your pencil.
For differentiability, the function must be smooth without any sharp points or instantaneous changes in slope.
In this example, the function is continuous at x = a because the limit as x approaches a from both sides equals f(a).
If there is a hole at x = 0 but f(a) is defined, the function is not continuous if the left-hand limit does not equal the right-hand limit.
A function with a hole where f(a) is defined but the limit does not equal f(a) is discontinuous.
In order for a function to be continuous at a point, the limit as x approaches that point must exist and be equal to the function's value at that point.
Transcripts
Browse More Related Video

BusCalc 16 Continuity and Differentiability

AP Calculus AB: Lesson 2.5 Differentiability

AP Calculus Review Three Theorems You Must Know (EVT, IVT, MVT)

Proof: Differentiability implies continuity | Derivative rules | AP Calculus AB | Khan Academy

Is the function continuous?
Continuity and Differentiability
5.0 / 5 (0 votes)
Thanks for rating: