The Normal Distribution and the 68-95-99.7 Rule

patrickJMT
11 Sept 201008:10
EducationalLearning
32 Likes 10 Comments

TLDRThis video explains the 68-95-99.7 rule of the normal distribution, using IQ scores as an example. It clarifies that 68% of observations fall within one standard deviation of the mean, 95% within two, and 99.7% within three. The video demonstrates how to apply this rule to determine the percentage of people with IQs above 100, above 145, and below 85, highlighting the rarity of extreme scores and the prevalence of scores close to the mean.

Takeaways
  • πŸ“š The video discusses the 68-95-99.7 rule for normal distributions, which is a statistical concept that describes the distribution of data points in a normal (bell-shaped) curve.
  • πŸ“ˆ The rule states that in a normal distribution, approximately 68% of data points fall within one standard deviation (Οƒ) of the mean (ΞΌ).
  • πŸ” For a normal distribution, about 95% of data points are within two standard deviations of the mean, according to the 68-95-99.7 rule.
  • 🌐 It is mentioned that 99.7% of data points in a normal distribution fall within three standard deviations of the mean.
  • 🧠 The video uses an IQ test as an example, where the scores are approximately normally distributed with a mean of 100 and a standard deviation of 15.
  • πŸ€” The video aims to calculate the percentage of people with IQ scores above 100, above 145, and below 85 using the 68-95-99.7 rule.
  • πŸ“‰ It is explained that about 50% of the observations are above the mean (100 in this case) and 50% are below, without the need for the rule.
  • πŸ“Š The video demonstrates how to calculate the percentage of IQ scores above 145 by considering three standard deviations from the mean.
  • πŸ“‰ The video concludes that approximately 0.15% of the population has an IQ score above 145, which is a very rare occurrence.
  • πŸ“ˆ The video also calculates that about 16% of the test scores are below 85, using the 68-95-99.7 rule and the symmetry of the normal distribution.
  • πŸ”‘ The takeaway is that knowing the mean, standard deviation, and the 68-95-99.7 rule can provide valuable insights into the distribution of scores or data points in a normal distribution.
Q & A

  • What is the 68-95-99.7 rule in the context of normal distribution?

    -The 68-95-99.7 rule, also known as the empirical rule, states that for a normal distribution, approximately 68% of the data falls within one standard deviation (Οƒ) of the mean (ΞΌ), 95% within two standard deviations, and 99.7% within three standard deviations.

  • What is the significance of the mean (ΞΌ) in a normal distribution?

    -The mean (ΞΌ) is the central value in a normal distribution, and it represents the average value of the data set. Half of the data is expected to be above the mean, and the other half below it.

  • What is the significance of the standard deviation (Οƒ) in a normal distribution?

    -The standard deviation (Οƒ) measures the amount of variation or dispersion in a set of values. In a normal distribution, it indicates how spread out the data is around the mean.

  • How is the normal distribution of IQ scores used in the video script?

    -The video script uses the normal distribution of IQ scores, which are approximately normally distributed with a mean of 100 and a standard deviation of 15, to apply the 68-95-99.7 rule and determine the percentage of people with IQ scores above 100, above 145, and below 85.

  • What percentage of people have an IQ score above 100 according to the script?

    -Approximately 50% of people have an IQ score above 100, as half of the observations are expected to be above the mean in a normal distribution.

  • What percentage of IQ scores are between 85 and 115?

    -Approximately 68% of IQ scores are between 85 and 115, which is within one standard deviation of the mean (100).

  • What percentage of IQ scores are between 70 and 130?

    -Approximately 95% of IQ scores are between 70 and 130, which is within two standard deviations of the mean (100).

  • What percentage of IQ scores are above 145?

    -Approximately 0.15% of the population has an IQ score above 145, which is more than three standard deviations above the mean.

  • What percentage of IQ scores are below 85?

    -Approximately 16% of the test scores are below 85, which is outside one standard deviation below the mean.

  • How can the 68-95-99.7 rule be used to understand the distribution of a set of data?

    -The 68-95-99.7 rule can be used to estimate the proportion of data that falls within certain intervals around the mean in a normal distribution. It helps to understand the spread and concentration of data points relative to the mean and standard deviation.

  • What is the practical application of knowing the percentage of IQ scores above certain thresholds?

    -Knowing the percentage of IQ scores above certain thresholds can help in understanding the rarity or commonality of high or low IQ scores, which can be useful in various fields such as education, psychology, and human resources for talent identification and development.

Outlines
00:00
πŸ“Š Introduction to the 68-95-99.7 Rule

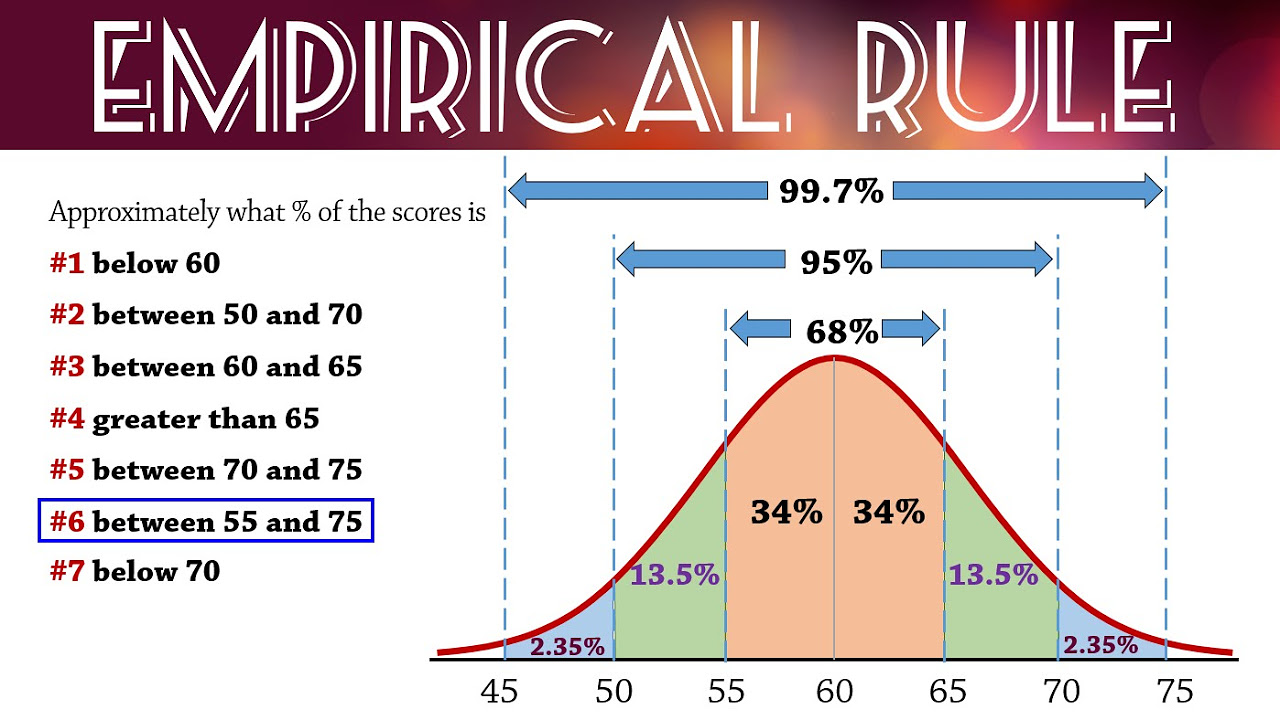
This paragraph introduces the concept of the 68-95-99.7 rule in the context of the normal distribution, also known as the bell curve. It explains that for a normal distribution with a mean (mu) and a standard deviation (Sigma), approximately 68% of observations fall within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations. The paragraph uses the example of an IQ test, which is normally distributed with a mean of 100 and a standard deviation of 15, to illustrate how the rule can be applied to determine the percentage of people scoring above or below certain IQ levels.

05:01
🧠 Applying the Rule to IQ Scores

The second paragraph delves into applying the 68-95-99.7 rule to the distribution of IQ scores. It explains how to calculate the percentage of people scoring above 100, above 145, and below 85 using the rule. The explanation includes the process of adding and subtracting the standard deviation from the mean to find the intervals within which the specified percentages of the population fall. The paragraph also provides a visual representation of the normal distribution curve and discusses the symmetry of the distribution, highlighting that 50% of the observations are above the mean and 50% are below. It concludes with the calculation that 0.15% of the population has an IQ score above 145 and that 16% of scores are below 85 or above 115, emphasizing the rarity of extreme IQ scores.

Mindmap
Keywords
πŸ’‘Normal Distribution
Normal distribution, also known as Gaussian distribution, is a probability distribution that is characterized by a symmetrical bell-shaped curve. In the context of the video, it is used to describe the distribution of IQ scores around the mean value. The video script explains how the majority of observations (IQ scores) fall within certain ranges of the mean, which is a fundamental concept in statistics for understanding data spread and variability.
πŸ’‘68-95-99.7 Rule
The 68-95-99.7 rule, also known as the empirical rule, is a shorthand for the percentages of values that lie within a certain number of standard deviations from the mean in a normal distribution. The video uses this rule to estimate the proportion of IQ scores within one, two, and three standard deviations from the mean, which helps in understanding the distribution of scores and the rarity of extreme scores.
πŸ’‘Mean (mu)
The mean, often represented by the Greek letter mu (ΞΌ), is the average value of a data set. In the video, the mean IQ score is given as 100, serving as the central point around which the distribution of IQ scores is symmetrically arranged. The mean is crucial for applying the 68-95-99.7 rule to determine the proportion of scores within different ranges.
πŸ’‘Standard Deviation (Sigma)
Standard deviation, represented by the Greek letter sigma (Οƒ), is a measure of the amount of variation or dispersion in a set of values. In the video, the standard deviation of IQ scores is 15, indicating how spread out the scores are from the mean. The video uses the standard deviation in conjunction with the mean to apply the 68-95-99.7 rule.
πŸ’‘IQ Test
An IQ test is a standardized measure of cognitive abilities, and the video script uses it as an example to illustrate the application of the normal distribution and the 68-95-99.7 rule. The script mentions that IQ scores are approximately normally distributed with a mean of 100 and a standard deviation of 15, which is the basis for the statistical analysis presented.
πŸ’‘Observations
In the context of the video, observations refer to the individual IQ scores that are being analyzed. The script discusses how a certain percentage of these observations fall within specific ranges defined by the standard deviations from the mean, illustrating the concept of data distribution in a normal distribution.
πŸ’‘Symmetry
Symmetry in a normal distribution context means that the data distribution is mirrored around the mean. The video script mentions that the distribution should be symmetric but acknowledges slight imperfections due to manual calculations. This concept is important for understanding how data is evenly distributed on both sides of the mean.
πŸ’‘Percentile
A percentile is a measure that indicates the value below which a given percentage of observations fall. The video uses percentiles to discuss the proportion of IQ scores above certain thresholds, such as 100, 145, and below 85, providing insights into the rarity or commonality of scores in specific ranges.
πŸ’‘Tail
In the context of a normal distribution, the tails refer to the extreme ends of the distribution, beyond the standard deviations from the mean. The video script uses the term to describe the small percentage of observations (0.15%) that fall outside three standard deviations from the mean, indicating very rare occurrences.
πŸ’‘Deviation
Deviation in the video script refers to the distance of a data point from the mean, measured in terms of standard deviations. The script discusses moving one, two, or three standard deviations away from the mean to determine the range of IQ scores that encompass 68%, 95%, and 99.7% of the observations, respectively.
πŸ’‘Statistical Significance
Statistical significance in the video is implied through the discussion of the percentages of IQ scores that fall within certain ranges. It helps to understand the likelihood of observing scores in those ranges and the rarity of extreme scores, such as those above 145 or below 55, which are statistically significant due to their low occurrence.
Highlights

Introduction to the normal distribution and the 68-95-99.7 rule.

Explanation of the 68-95-99.7 rule for normal distributions, relating to the mean (ΞΌ) and standard deviation (Οƒ).

68% of observations fall within one standard deviation of the mean in a normal distribution.

95% of observations fall within two standard deviations of the mean.

99.7% of observations fall within three standard deviations of the mean.

Application of the rule using IQ test scores as an example, with a mean of 100 and a standard deviation of 15.

50% of people have IQ scores above 100 due to the symmetry of the normal distribution.

Calculating the percentage of people with IQ scores above 145 using the 68-95-99.7 rule.

Approximately 0.15% of the population has an IQ score above 145.

16% of test scores are below 85, outside one standard deviation from the mean.

16% of test scores are above 115, outside one standard deviation from the mean.

Demonstration of the normal distribution curve with the mean at 100 and standard deviation of 15.

The importance of knowing the mean, standard deviation, and the 68-95-99.7 rule for understanding score distributions.

The rule's practical application in estimating the percentage of scores within specific ranges.

Visual representation of the normal distribution curve with the calculated ranges for one, two, and three standard deviations.

Explanation of how the tails of the normal distribution represent the rarest scores.

The significance of the 68-95-99.7 rule in understanding the spread of data in a normal distribution.

Final summary of the 68-95-99.7 rule's utility in estimating the distribution of IQ scores.

Transcripts

Browse More Related Video

What is a Bell Curve or Normal Curve Explained?

Statistics - How to use the Empirical Rule

Empirical Rule of Standard Deviation in Statistics

The Normal Distribution and the 68-95-99.7 Rule (5.2)

Empirical Rule (68-95-99.7) for Normal Distributions

k12.org exercise: Standard normal distribution and the empirical | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Normal DistributionIQ TestStatistical RuleBell CurveStandard DeviationMean ValueObservation PercentageData AnalysisProbability TheoryEducational Content