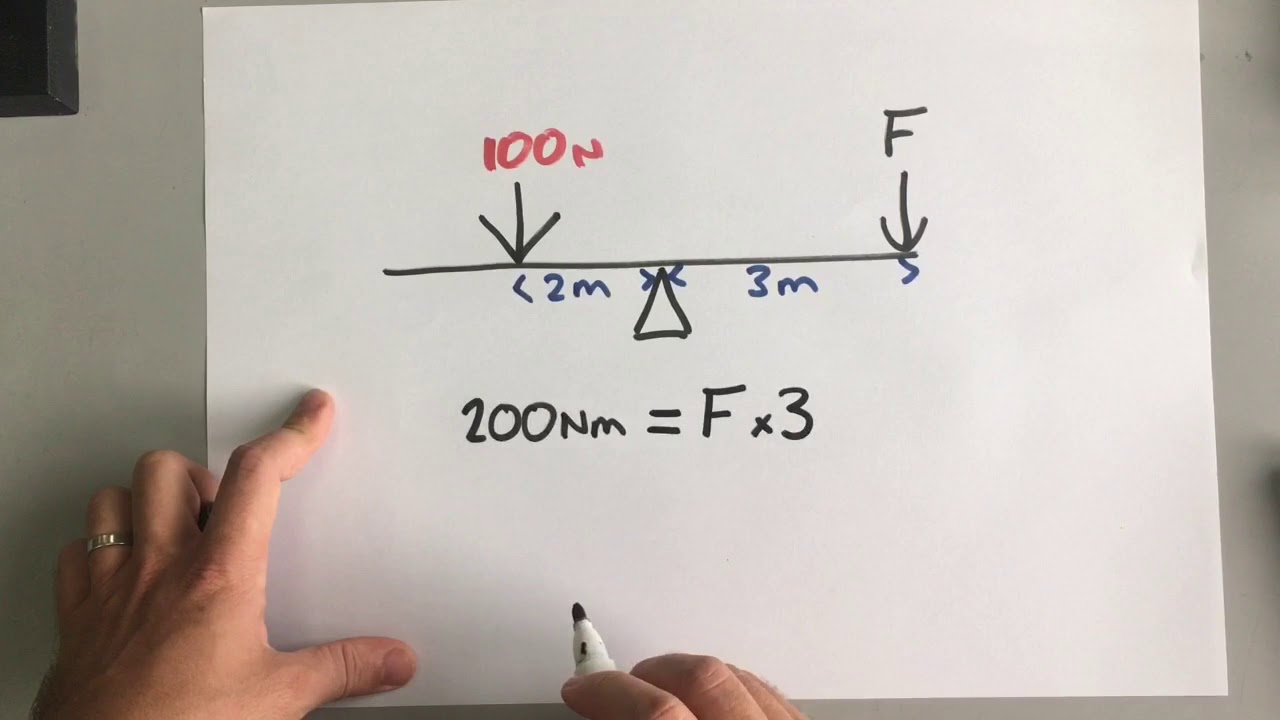
The Principle of Moments - A Level Physics
TLDRThe video discusses the concept of moments, which are the turning effects produced by applying a force at a certain distance from an axis of rotation. Using an Allen key as an example, it explains how a small force applied over a long distance can create a large moment. The video covers the textbook definition of a moment (force multiplied by perpendicular distance) and explores how to calculate moments when forces act at angles. It also introduces the principle of moments, stating that for rotational equilibrium, the sum of anticlockwise moments equals the sum of clockwise moments.
Takeaways
- 🔧 The video discusses the concept of moment, which is the turning effect produced by a force applied at a distance from an axis of rotation.
- 🛠️ An Allen key is used as an example of a force multiplier, allowing a small force applied over a long distance to create a large moment.
- 📚 The textbook definition of moment is the force multiplied by the perpendicular distance from the line of action of the force to the axis or point of rotation.
- 📏 Symbolically, moment is represented by a capital M, with force denoted by F and distance by X, so moment (M) equals F times X.
- ⚖️ The script introduces the idea of solving for moment when a force is acting at an angle, creating a more complex scenario than a straightforward vertical force.
- 📐 The importance of drawing a diagram to visualize and solve moment problems involving forces at an angle is emphasized.
- 📐 To find the moment when a force is at an angle, one can use the perpendicular distance from the line of action to the pivot, calculated using trigonometry (cos Theta).
- 📚 The moment can be calculated as the force (F) times the perpendicular distance (x') from the pivot to the line of action, which is F times X times cos Theta.
- 🔄 The script also explains an alternative approach by resolving the force into its vertical component and then calculating the moment based on this component.
- ⚖️ The principle of moments for rotational equilibrium is introduced, stating that the sum of anticlockwise moments equals the sum of clockwise moments, indicating balance.
- 🏋️♂️ A large moment does not necessarily mean an object will rotate; equilibrium can exist with counterbalancing moments, as demonstrated with the example of a boulder and a digger.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is the concept of moments and how force applied at a distance from an axis of rotation creates a turning effect, known as a moment.
How is an Allen key used as a force multiplier?
-An Allen key is used as a force multiplier by applying a small force at a long distance from the pivot point, creating a large moment which helps in tightening or loosening bolts.
What is the textbook definition of a moment?
-The textbook definition of a moment is the force multiplied by the perpendicular distance from the line of action of the force to the axis or the point of rotation.
What symbols are used to represent moment and force in the video?
-A capital 'M' is used to represent moment, a lowercase 'm' for mass, and 'F' for force.
How do you calculate the moment when a force is acting at an angle?
-To calculate the moment when a force is acting at an angle, you use the formula: Moment = F * X * cos(Theta), where F is the force, X is the distance from the pivot, and Theta is the angle of the force.
What is the importance of drawing a diagram when solving problems involving forces and moments?
-Drawing a diagram is crucial as it helps visualize the forces, distances, and angles involved, making it easier to apply the correct formulas and understand the problem better.
How do you find the perpendicular distance in the context of moments?
-The perpendicular distance is found by using trigonometric functions. If the force is at an angle, you can calculate the perpendicular distance by multiplying the distance X by cos(Theta).
What is the principle of moments for a body in rotational equilibrium?
-The principle of moments states that for a body in rotational equilibrium, the sum of the anticlockwise moments is equal to the sum of the clockwise moments.
Why doesn't a large moment necessarily mean that an object will start rotating?
-A large moment doesn't necessarily mean an object will start rotating because there may be other moments acting on the object that keep it in equilibrium, such as opposing moments that balance each other out.
What role does the angle Theta play in calculating the moment of a force?
-The angle Theta determines the component of the force that acts perpendicular to the distance from the pivot. It is used in the cosine function to calculate the effective perpendicular distance, which is essential for determining the moment.
Outlines
🔧 Understanding Moments and Force Multipliers
This paragraph introduces the concept of a moment, which is the turning effect produced by a force applied at a distance from an axis of rotation. The video script uses an allen key as an example of a force multiplier, explaining how applying a small force over a long distance can create a large moment, effectively loosening or tightening a bolt. The textbook definition of moment is given as the force multiplied by the perpendicular distance from the line of action of the force to the axis or point of rotation. The symbols for moment (capital M) and force (F) are introduced, along with the formula for calculating moment (M = F * X). The paragraph also touches on the concept of equilibrium, where vertical forces and distances are considered in balance.
📐 Calculating Moments with Forces at Angles
The second paragraph delves into the complexities of calculating moments when forces are applied at angles rather than directly vertically. It explains two methods for solving such problems: one involves using the cosine of the angle (theta) to find the perpendicular distance from the line of action to the pivot, resulting in the moment formula M = F * X * cos(Theta). The other method involves resolving the force into its vertical component and calculating the moment based on this component. The paragraph emphasizes the importance of drawing diagrams and understanding the geometry of the situation, including the use of right-angle triangles and trigonometric relationships. It also discusses the principle of moments, stating that for rotational equilibrium, the sum of anticlockwise moments must equal the sum of clockwise moments, indicating a state of balance without rotation.
Mindmap
Keywords
💡Bolt
💡Allen Key
💡Moment
💡Force Multiplier
💡Textbook Definition
💡Symbols
💡Right Angle Triangle
💡Cosine
💡Equilibrium
💡Principle of Moments
Highlights
Introduction to the concept of moment and its relation to force applied at a distance from an axis of rotation.
Explanation of using an Allen key as a force multiplier to tighten or loosen bolts.
Textbook definition of moment as force multiplied by the perpendicular distance from the line of action to the axis of rotation.
Symbol representation of moment with capital M and force with F, and the formula M = F * X.
Discussion on the balance of forces in equilibrium with examples of large and small forces at different distances.
Introduction of a more complex scenario where force is applied at an angle to the vertical.
Emphasis on the importance of drawing diagrams to solve problems involving forces at an angle.
Use of trigonometry to find the perpendicular distance from the line of action to the pivot (x' = X * cos Theta).
Calculation of moment when force is applied at an angle using the formula M = F * X * cos Theta.
Alternative approach to resolve the force into its vertical component and calculate the moment.
Explanation of the special case when force is vertical (Theta = 0) and cos Theta equals one.
Clarification that a large moment does not necessarily mean an object will rotate, introducing the concept of equilibrium.
Introduction of the principle of moments for rotational equilibrium and its significance.
Summary of the principle of moments stating that the sum of anticlockwise moments equals the sum of clockwise moments.
Illustration of equilibrium with an example of a heavy boulder and a digger, emphasizing the balance of moments.
Final note on the importance of considering all moments acting on a body to understand its rotational state.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: