GCSE Physics - How Moments Work - Spanners and Seesaws #46

Cognito
17 Nov 201905:40
EducationalLearning
32 Likes 10 Comments

TLDRIn today's video, we explore the concept of moments, which explain why longer spanners are easier to use than shorter ones and how people of different weights can balance on a seesaw. A moment is the rotational effect of a force, calculated as the force multiplied by the perpendicular distance from the pivot. The video demonstrates how to calculate moments using real-life examples, such as applying force to a spanner and balancing a seesaw. Key concepts include the importance of perpendicular distance and balancing multiple moments acting on an object.

Takeaways
  • 🔧 A moment is the rotational or turning effect of a force, which can be described as force times the perpendicular distance from the pivot.
  • 📐 The size of a moment is calculated using the equation: Moment = Force x Perpendicular Distance from the pivot.
  • 🔨 Using a longer spanner is easier because it provides a greater moment due to the increased distance from the pivot, making it easier to tighten or loosen nuts.
  • ⚖️ The perpendicular distance is crucial; it must be measured at right angles to the direction of the force applied.
  • 📏 Applying force at an angle reduces the perpendicular distance and thus the moment, making it less effective.
  • 🔢 An example calculation is provided: applying an 80 Newton force 20 cm (0.2 meters) from the pivot results in a moment of 16 Newton meters.
  • 🔄 If the same moment is desired at a closer distance to the pivot, a greater force is required, as demonstrated by needing 160 Newtons at 0.1 meters from the pivot.
  • 🤹‍♂️ Multiple moments can act on an object simultaneously, such as on a seesaw, where the moments from different sides must be compared.
  • ⚖️ The seesaw balances when the total anticlockwise moment equals the total clockwise moment, resulting in no net movement.
  • 🧭 To balance a seesaw, the force must be applied at a distance calculated by dividing the moment by the force, as shown in the script with an 800 Newton force needing to be 1.5 meters from the pivot to balance a 1200 Newton meter moment.
  • 👋 The video concludes with the hope that the information on moments was useful and invites viewers to return for more content.
Q & A

  • What is a moment in the context of the video?

    -A moment is the rotational or turning effect of a force, which can be described as the tendency of an object to rotate around a pivot point when a force is applied.

  • How is the size of a moment calculated?

    -The size of a moment is calculated using the equation where moment equals the force applied times the perpendicular distance from the pivot to the point where the force is applied.

  • Why is it important to use the perpendicular distance in calculating a moment?

    -The perpendicular distance is important because it measures the effective distance at a right angle to the direction of the force, which directly contributes to the turning effect.

  • If you apply an 80 Newton force to a spanner 20 centimeters from the pivot, what moment is generated?

    -First, convert 20 centimeters to meters (0.2 meters). Then, multiply 0.2 meters by 80 Newtons to get a moment of 16 Newton meters.

  • What would be the required force to generate the same moment of 16 Newton meters, but 0.1 meters from the pivot?

    -Rearranging the moment equation to force = moment / distance, and plugging in 16 Newton meters and 0.1 meters, the required force would be 160 Newtons.

  • Why does applying a force closer to the pivot require a larger force to achieve the same moment?

    -Applying a force closer to the pivot results in a smaller perpendicular distance, which means a larger force is needed to achieve the same turning effect or moment.

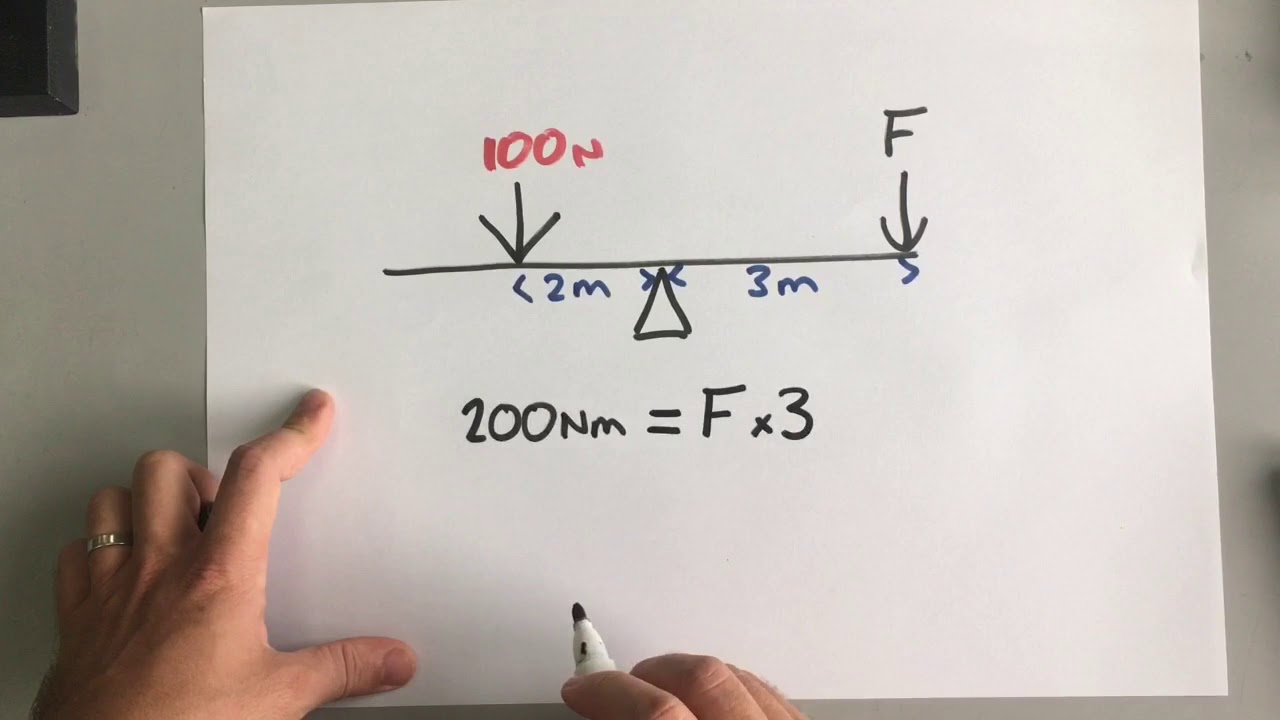
  • What is the significance of moments in the context of a seesaw?

    -In the context of a seesaw, moments are crucial because they determine the balance and movement of the seesaw. Each side of the seesaw can have a moment that can be clockwise or anti-clockwise, and the seesaw's movement depends on the comparison of these moments.

  • How can you determine if a seesaw will remain balanced?

    -A seesaw will remain balanced if the total anticlockwise moment equals the total clockwise moment, meaning they perfectly balance each other out.

  • If a seesaw has a total clockwise moment of 1200 Newton meters, how far from the pivot should an 800 Newton force be applied to balance it?

    -Using the rearranged equation distance = moment / force, 1200 Newton meters divided by 800 Newtons gives a distance of 1.5 meters from the pivot.

  • Why do we talk about moments in terms of clockwise or anti-clockwise rather than up or down?

    -We talk about moments in terms of clockwise or anti-clockwise because these terms describe the direction of the turning effect, which is more relevant to the rotational motion of an object than vertical or horizontal directions.

  • What did the video aim to teach about moments and their applications?

    -The video aimed to teach the concept of moments, how they are calculated, and their applications in everyday scenarios like using a spanner and balancing on a seesaw, emphasizing the importance of force and distance in creating a turning effect.

Outlines
00:00
🔧 Understanding Moments and their Calculation

This paragraph introduces the concept of a moment, which is the rotational effect of a force. It explains that a moment is created when a force is applied at a distance from a pivot point, causing a turning effect. The formula for calculating the moment is given as the force multiplied by the perpendicular distance from the pivot. The importance of perpendicular distance is emphasized, and an example calculation is provided using an 80 Newton force applied 20 centimeters from the pivot, resulting in a 16 Newton-meter moment. The paragraph also discusses the necessity of comparing moments when multiple forces are acting on an object, such as a seesaw, and how to balance these moments to achieve equilibrium.

05:03
📏 Balancing Moments on a Seesaw

The second paragraph delves into the application of moments in the context of a seesaw, where the pivot is at the center. It illustrates how to calculate the moment created by a force applied to one side of the seesaw and contrasts it with the moment on the opposite side to maintain balance. The paragraph provides a step-by-step explanation of how to rearrange the moment equation to find the distance required for a force to balance the seesaw, using the example of an 800 Newton force needing to be 1.5 meters from the pivot to counteract a 1200 Newton-meter clockwise moment. The summary concludes with the concept that if the total moments in both directions are equal, the seesaw will remain stationary due to the balance of forces.

Mindmap
Keywords
💡Moment
In the context of the video, 'moment' refers to the rotational or turning effect of a force. It is a fundamental concept in physics that helps explain why certain tools or mechanisms work effectively. The video defines moment as the product of the force applied and the perpendicular distance from the pivot point, which is crucial for understanding how to maximize the turning effect in various scenarios, such as using a spanner or balancing on a seesaw.
💡Spanner
A 'spanner' is a tool used to grip and turn nuts or bolts. The video uses the spanner as an example to illustrate the concept of moment. It explains that a longer spanner is easier to use because the force applied at the end of the spanner creates a larger moment when further from the pivot, making it more effective in turning the nut.
💡Pivot
The 'pivot' is the central point around which an object turns. In the video, the pivot is used to describe the point around which the spanner turns when a force is applied. Understanding the role of the pivot is essential for calculating the moment and determining the effectiveness of the turning force.
💡Force
'Force' in the video is the push or pull applied to an object, such as the downward force on a spanner. The video explains that the magnitude and direction of the force, as well as its distance from the pivot, are key factors in determining the moment and the object's rotational effect.
💡Perpendicular Distance
The 'perpendicular distance' is the distance measured at a right angle to the direction of the force applied. The video emphasizes its importance in calculating the moment, as it must be the shortest distance from the pivot to the point of force application, ensuring the maximum turning effect.
💡Newton
A 'newton' is the unit of force in the International System of Units (SI). The video uses newtons to quantify the force applied to the spanner, demonstrating how the force's magnitude affects the moment generated and the object's rotational movement.
💡Newton Meters
'Newton meters' is the unit used to measure moment. The video shows that moment is calculated by multiplying the force in newtons by the perpendicular distance in meters, resulting in a moment measured in newton meters, which indicates the turning effect's strength.
💡Seesaw
A 'seesaw' is a type of lever used for play or as a simple machine, often used to demonstrate the principle of moments. The video explains how moments on a seesaw can be calculated and balanced, with the pivot being the middle point, and the forces and their distances from the pivot determining the seesaw's movement.
💡Clockwise/Anti-Clockwise
The terms 'clockwise' and 'anti-clockwise' are used in the video to describe the direction of the turning effect created by the moments. This is important when considering the balance of a seesaw, as moments in opposite directions can either cause movement or balance each other out.
💡Balance
'Balance' in the video refers to the state where the total clockwise moment equals the total anti-clockwise moment, resulting in no net movement. The video uses the seesaw example to illustrate how balance is achieved by adjusting the force and its distance from the pivot.
Highlights

The video explains moments as the rotational or turning effect of a force.

A longer spanner is easier to use because it creates a larger moment due to the increased distance from the pivot.

Different weights can balance on a seesaw by adjusting the perpendicular distance from the pivot.

The moment is calculated using the equation: moment = force × perpendicular distance from the pivot.

Applying a force far away from the pivot maximizes the moment.

Perpendicular distance is crucial and means measuring at a right angle to the force's direction.

Applying force at an angle reduces the perpendicular distance and thus the moment.

An example calculation is provided to find the moment with an 80 Newton force applied 20 cm from the pivot.

To achieve the same moment with a different distance, the force required can be calculated by rearranging the moment equation.

A seesaw is used as an example to illustrate the concept of multiple moments acting on the same object.

The direction of moments is described in terms of clockwise or anti-clockwise rather than up or down.

The overall movement of a seesaw is determined by comparing the magnitudes of clockwise and anti-clockwise moments.

If two moments are equal in magnitude, they balance each other out, resulting in no movement.

To balance a seesaw, the force must be applied at a specific distance from the pivot, calculated using the moment equation.

The video concludes with an example of balancing a seesaw with an 800 Newton force at a calculated distance.

The video aims to provide a useful understanding of moments and their practical applications.

Transcripts

Browse More Related Video

The Principle of Moments - A Level Physics

Moments, Torque, Toppling & Couples - GCSE & A-level Physics (full version)

Turning Forces (Moments)

GCSE Physics - Forces 5 - Moments and Centre of Mass

Principle of Moments - Physics Revision

Moments (part 2) | Moments, torque, and angular momentum | Physics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsMomentsRotational EffectSpannerSeesawBalanceForcePivotDistanceEquilibrium