AP Calculus AB: Lesson 6.1 Finding Antiderivatives
TLDRIn this educational video, Michelle Crummel teaches the concept of anti-derivatives, focusing on polynomial type functions. She explains how to identify these functions and use the power rule in reverse to find anti-derivatives. Michelle demonstrates the process with various examples, including handling special cases like 1/x and square root of x, and emphasizes the importance of the constant of integration. She also covers practical applications, such as modeling the growth of shrubs and the motion of a particle, showcasing the relevance of anti-derivatives in real-world scenarios.
Takeaways
- 📚 The video is a tutorial on finding anti-derivatives of functions, specifically for polynomial-type functions.
- 🔍 The script defines polynomial-type functions as those where each term is a constant multiplied by a variable raised to a constant power, including constant terms as \( x^0 \).
- 📉 The video distinguishes between polynomial-type functions and actual polynomial functions, noting that the latter cannot have negative exponents.
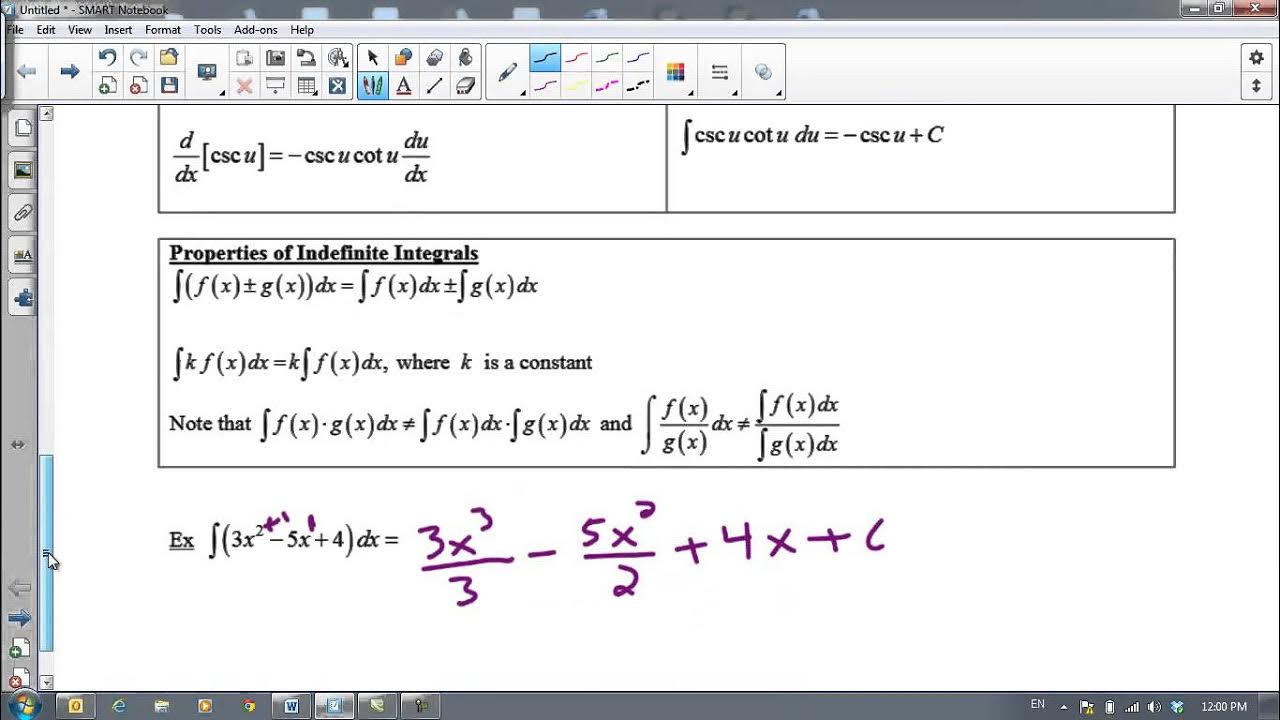
- 🔄 The process of finding anti-derivatives involves reversing the steps of the power rule used for differentiation.
- ➕ To find the anti-derivative, one should add 1 to the exponent of the term and then divide by the new exponent.
- 🔍 The script explains the importance of the constant of integration (\( +C \)) in anti-derivatives, which serves as a placeholder for unknown constant terms.
- 📈 The video provides examples of finding anti-derivatives for various functions, emphasizing the method of reversing the power rule.
- 🤔 The script highlights the potential confusion that can arise from derivatives of constants and the importance of considering the original function form.
- 📝 It demonstrates the process of integrating more complex functions by rewriting them into polynomial-type forms, where possible.
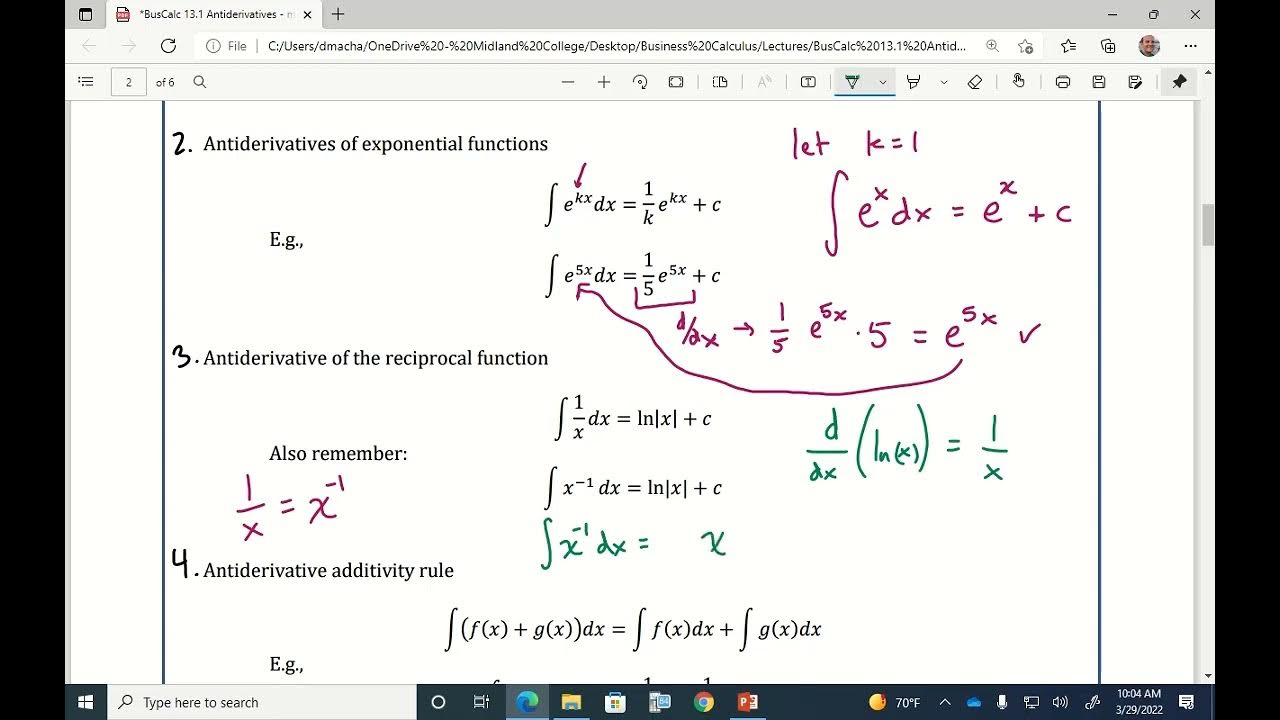
- 🧩 The video also touches on anti-derivatives of non-polynomial functions like \( \frac{1}{x} \), which requires special recognition and memorization of certain forms.
- 🔚 The tutorial concludes with practical applications of anti-derivatives, such as modeling the growth of shrubs and the motion of a particle, emphasizing the connection between derivatives and real-world rates of change.
Q & A
What is the main topic of the video?
-The main topic of the video is to teach viewers how to find the anti-derivative of a function, including identifying polynomial type functions and using the power rule to find anti-derivatives.
What is the definition of a polynomial type function according to the video?
-A polynomial type function is defined as a function where each term is in the form of a constant multiplied by a variable raised to some constant power, but it does not necessarily have to be a polynomial function due to the limitations on the definition of a polynomial.
Why can't all polynomial type functions be called polynomial functions?
-Not all polynomial type functions can be called polynomial functions because polynomial functions have specific limitations, such as not containing negative exponents and having whole numbers as their exponents, which are zero or more.
How does the video explain the process of finding the anti-derivative of a function?
-The video explains the process by reversing the steps of the power rule used for differentiation. This involves adding 1 to the exponent and then dividing by the new exponent.
What is the purpose of the constant of integration, 'c', in anti-derivatives?
-The constant of integration, 'c', is used as a placeholder in anti-derivatives because when reversing a derivative, the original constant term of the function is unknown and cannot be determined without additional information.
How does the video use the derivative of a function to find its anti-derivative?
-The video uses the derivative of a function to find its anti-derivative by applying the reverse power rule, which involves adjusting the exponents of the terms in the derivative and then adding the constant of integration.
What is the significance of the natural log function in anti-derivatives, as mentioned in the video?
-The natural log function is significant in anti-derivatives because it is the anti-derivative of the function 1/x, which is a common form that arises when dealing with anti-derivatives of inverse proportional functions.
How does the video handle the anti-derivative of functions that are not in polynomial type form?
-The video suggests rewriting the function into polynomial type form if possible, and if not, using recognition and memorization of specific anti-derivatives, such as the natural log for 1/x.
What is the role of the reverse power rule in finding anti-derivatives of polynomial type functions?
-The reverse power rule plays a crucial role in finding anti-derivatives of polynomial type functions by providing a systematic method to reverse the differentiation process and find the original function.
Can the quotient rule for derivatives be used to find anti-derivatives?
-No, the quotient rule for derivatives does not have a direct counterpart for finding anti-derivatives. Instead, functions need to be rewritten into polynomial type form or other recognized forms to apply the reverse power rule or other anti-derivative techniques.
How does the video address the anti-derivative of functions involving trigonometric functions like sine and cosine?
-The video addresses the anti-derivative of trigonometric functions by stating that the anti-derivative of cosine is sine and the anti-derivative of negative sine is cosine, with the inclusion of the constant of integration for each.
Outlines
📚 Introduction to Anti-derivatives and Polynomial Functions
Michelle Crummel introduces the concept of anti-derivatives, explaining how they are the reverse process of differentiation. She clarifies the difference between polynomial functions and polynomial-type functions, emphasizing that the latter includes any term in the form of a constant times a variable raised to a constant power, even if the power is not a whole number. The video will focus on finding anti-derivatives for polynomial-type functions using the power rule in reverse.
🔍 Identifying Polynomial-Type Functions and Their Derivatives
The script delves into identifying which given functions are polynomial-type by examining their terms. It explains how to rewrite non-standard terms into the polynomial form and discusses the limitations of polynomial functions, such as not containing negative exponents. The process of finding derivatives using the power rule is also reviewed, setting the stage for understanding how to find anti-derivatives by reversing these steps.
📝 The Process of Finding Anti-derivatives for Polynomial-Type Functions
Michelle demonstrates how to find anti-derivatives by reversing the power rule used in differentiation. This involves adding one to the exponent and then dividing by the new exponent. She applies this method to several equations, emphasizing the importance of including a constant of integration (+C) due to the indefinite nature of the original function's constant term.
🤔 Special Cases in Anti-derivative Calculations
The script addresses special cases in anti-derivative calculations, such as when the function is not in polynomial form or when it involves terms like 1/x. It explains the need for recognizing equivalent forms and using alternative methods, such as the natural logarithm for 1/x, to find anti-derivatives. The importance of domain matching when dealing with functions like ln(x) is highlighted.
📚 Expanding and Simplifying Expressions for Anti-derivatives
The video script covers the process of expanding and simplifying expressions to find their anti-derivatives. It shows how to rewrite complex expressions into polynomial-type forms and then apply the reverse power rule. The script also discusses the product rule for derivatives and how it does not have a direct counterpart for anti-derivatives, necessitating the expansion of products into simpler terms.
🧩 Integrating Functions with Trigonometric Components
Michelle provides examples of integrating functions that include sine and cosine components. She explains the straightforward anti-derivatives of cosine and sine functions and emphasizes the importance of checking work by differentiating the anti-derivative to ensure it matches the original function. The script also includes integrating a combination of sine and cosine functions with constant multiples.
🔄 Solving for Functions Given Second Derivatives
The script presents a method for solving for a function's equation when given its second derivative. It involves integrating the second derivative to find the first derivative and then integrating again to find the original function, using the constant of integration at each step. An example is provided where the function's value at a specific point is known, allowing for the determination of the constant of integration.
🌳 Applying Anti-derivatives to Real-World Problems: Plant Growth Rates
An application of anti-derivatives is shown in the context of plant growth rates. The script describes how the growth rate of a shrub can be modeled by a differential equation and how to find the height of the shrub at different times by integrating the growth rate function. It includes an example where the initial height and the growth rate equation are given, and the height at a future time is calculated.
🚀 Motion Analysis with Anti-derivatives: Particle Velocity and Position
The final part of the script applies anti-derivatives to analyze the motion of a particle along the x-axis. It explains how to find the velocity and position of a particle given its acceleration and initial conditions. The script provides an example where the velocity function is given, and the position function is derived by integrating the velocity. The acceleration at a specific time is also calculated.
Mindmap
Keywords
💡Anti-derivative
💡Polynomial type function
💡Power rule
💡Constant of integration
💡Derivative
💡Exponential function
💡Integration
💡Quotient rule
💡Product rule
💡Trigonometric functions
Highlights
Introduction to finding anti-derivatives and determining polynomial type functions.
Definition of polynomial type functions as those where each term is a constant multiplied by a variable raised to a constant power.
Explanation of how to rewrite non-standard terms to fit the polynomial type function form using algebra.
Identification of functions that are not polynomial functions due to negative exponents.
Demonstration of how to find the anti-derivative by reversing the steps of the power rule.
Clarification on the difference between polynomial functions and polynomial type functions in the context of anti-derivatives.
Use of the power rule for derivatives and its reverse process for finding anti-derivatives of polynomial type functions.
Introduction of the constant of integration, 'c', as a placeholder for unknown constants in anti-derivatives.
Illustration of the process to find the anti-derivative of a given polynomial function using the reverse power rule.
Discussion on the importance of checking anti-derivative solutions by taking their derivatives.
Explanation of how to handle anti-derivatives of functions not in polynomial type form by rewriting them.
Special case handling of the anti-derivative of 1 over x using natural logarithms and absolute values.
Integration of functions involving products and quotients by transforming them into polynomial type form.
Application of anti-derivatives to real-world problems such as calculating the height of shrubs over time.
Use of anti-derivatives to determine the position of a particle given its velocity function.
Introduction to the concept of acceleration as the derivative of velocity and its calculation.
Final summary of the process for finding anti-derivatives and their applications in various contexts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: