Calculus AB Homework 5.5: Particle Motion Practice
TLDRThis educational video script guides viewers through solving physics problems involving motion along the x-axis. It covers concepts like velocity, acceleration, and position, using graphs and equations to determine when a particle moves right or left, changes direction, and calculates average velocity and acceleration. The script also addresses the application of these concepts to real-life scenarios like a cyclist's motion and runners on a track, providing a clear explanation of how to analyze velocity graphs and derive acceleration functions.
Takeaways
- 📚 The video covers homework problems 29 to 35 from Unit 5, focusing on the analysis of a particle's motion along the x-axis using position and velocity graphs.
- 📈 For problem 29, the particle moves to the right when the velocity is positive, which corresponds to the interval from 0 to 1 seconds on the position graph.
- 🔄 For problem 29 Part B, the particle moves to the left during intervals where the position graph is decreasing, specifically from 2 to 3 seconds and from 5 to 6 seconds.
- 📉 In problem 29 Part C, the velocity function is expressed as a piecewise function, with different slopes for different time intervals, and undefined at endpoints and corner points.
- ⏱️ Problem 29 Part D involves calculating the average velocity over the interval from 1 to 6 seconds by finding the change in position over the change in time.
- 🚴 Problem 30 examines a particle's motion with velocity given by a trigonometric function and requires determining the number of times the particle changes direction within a specified interval.
- 🔢 The video uses a graph to show that the particle changes direction three times on the interval from 0 to 5 seconds, excluding instances where the velocity is momentarily at rest without a sign change.
- 🏃 Problem 31 discusses Jeff's bicycle motion, with velocity graphed and the task of finding the velocity and acceleration at specific times, including when Jeff turns around.
- 📊 For problem 32, the video compares the velocities of two runners, A and B, using both a graph and an equation, and calculates their velocities and accelerations at T equals 2 seconds.
- 🚗 Problem 33 analyzes a car's motion from a velocity graph, determining intervals of positive acceleration, average acceleration over a time interval, and the car's speed changes at a specific time.
- 🏃♂️ Problem 34 compares the motion of two runners on a racetrack using a velocity graph for runner A and a velocity equation for runner B, finding their velocities and accelerations at T equals 2 seconds.
- 🔁 Problem 35 deals with an object moving with a velocity function based on a sine function, calculating the object's acceleration at T equals 4 and analyzing the velocity and speed changes between 3 and 4.5 seconds.
Q & A
What is the criterion for a particle to be moving to the right according to the video?
-The particle is moving to the right when the velocity is positive, which corresponds to the position function being increasing on the graph.
How can you determine the intervals of time when the particle is moving to the left?
-The particle is moving to the left when the velocity is negative, which means the position function is decreasing on the graph. The intervals are identified by looking for these decreases.
What is the piecewise function for velocity expressed in the video?
-The piecewise function for velocity is defined by different slopes of the position function graph at various intervals, with the velocity being undefined at endpoints and corner points where the position is not differentiable.
Why is the velocity undefined at certain points in the video?
-The velocity is undefined at endpoints and corner points because these are the points where the position function is not differentiable, indicating a change in direction or an instantaneous stop.
How is the average velocity calculated for the interval from 1 to 6 in the video?
-The average velocity is calculated by finding the change in position (P of 6 minus P of 1) and dividing it by the change in time (6 minus 1).
What does it mean for a particle to change direction according to the video?
-A particle changes direction when its velocity changes sign, moving from positive to negative or vice versa.
How many times does the particle change direction on the interval from 0 to 5 in the video?
-The particle changes direction three times on the interval from 0 to 5, as identified by the velocity function changing sign at specific points.
What is the value of the velocity at time T equals 2 in the second problem presented in the video?
-At time T equals 2, the velocity is approximately zero, indicating the particle is momentarily at rest but not changing direction.
What is the average acceleration between T equals 1 and T equals 3.5 seconds in the video?
-The average acceleration is calculated by finding the change in velocity (V of 3.5 minus V of 1) and dividing it by the change in time (3.5 minus 1), resulting in approximately 0.8 meters per second squared.
How does the video explain the difference between velocity and acceleration?
-The video explains that velocity is the rate of change of position, while acceleration is the rate of change of velocity. A change in the sign of the velocity function indicates a change in direction, whereas acceleration indicates how quickly the velocity is changing.
What is the significance of the velocity being zero at a certain point in time in the video?
-A velocity of zero at a certain point in time indicates that the particle is momentarily at rest. However, this does not necessarily mean the particle will change direction, as the velocity must change sign to indicate a change in direction.
Why does the video mention that Rolle's Theorem cannot be applied on the interval from 0 to 5?
-Rolle's Theorem requires three conditions: continuity on the interval, differentiability on the interval (except possibly at the endpoints), and the function values at the endpoints to be the same. The video explains that the velocity function fails two of these conditions on the interval from 0 to 5.
How does the video determine when Jeff starts moving away from his point of origin?
-The video determines that Jeff starts moving away from his point of origin when the velocity becomes negative, which occurs after time T equals 4 minutes.
What does the video conclude about the acceleration of the particle at T equals two in the last problem?
-The video concludes that at T equals two, the acceleration is approximately 1.588 meters per second squared, indicating that the particle is slowing down as the acceleration and velocity have opposite signs.
Outlines
📚 Particle Motion Analysis
This paragraph discusses a physics problem involving a particle's motion along the x-axis. The problem provides a graph of the particle's position function over time and asks several questions about the particle's motion. The analysis includes determining when the particle is moving to the right (when velocity is positive), when it is moving to the left (when velocity is negative), expressing velocity as a piecewise function, identifying when velocity is undefined, and calculating the average velocity over a given interval. Key points include understanding the relationship between position, velocity, and acceleration, and applying calculus concepts to determine motion characteristics.
📉 Direction Changes and Velocity Analysis
The second paragraph continues the physics theme, focusing on a particle's velocity given by a specific function. The task is to determine how many times the particle changes direction within a certain time interval and to explain the reasoning. The analysis involves looking for where the velocity function changes sign, indicating a change in direction. The paragraph also includes finding the velocity and acceleration at a specific time, using a calculator to determine the number of direction changes, and describing the particle's motion at a moment when it is momentarily at rest. The summary highlights the importance of understanding the mathematical representation of motion and the physical implications of velocity and acceleration.
🚴♂️ Jeff's Bicycle Velocity and Acceleration
This paragraph presents a scenario where Jeff is riding his bicycle to school, and his velocity is graphed over a 15 to 40-minute interval. The analysis requires finding the acceleration at a specific time and determining intervals where the acceleration is zero. It also discusses the application of Rolle's Theorem to the velocity graph to find points of zero acceleration. The summary explains the process of calculating the slope of the velocity graph to find acceleration, the conditions for applying Rolle's Theorem, and the interpretation of the graph to understand Jeff's motion, including when he turns around to head back home.
📈 Particle's Velocity and Acceleration Calculations
The fourth paragraph involves calculating the acceleration of a particle moving along the x-axis, given its velocity function. The task includes finding the acceleration at a specific time without using a calculator, understanding the relationship between velocity and acceleration, and determining when the particle is slowing down. The summary emphasizes the mathematical process of deriving acceleration from velocity, the physical interpretation of the signs of these quantities, and the conditions under which the particle's speed increases or decreases.
🏎️ Car's Velocity and Acceleration Graph Interpretation
This paragraph analyzes the velocity graph of a car traveling on a straight road, provided with both a graph and a table of values. The discussion includes determining when the car's acceleration is positive, finding the average acceleration over a specific interval, estimating acceleration at a particular time, and assessing whether the car's speed is increasing or decreasing at a given moment. The summary focuses on interpreting the velocity graph to understand the car's motion, calculating average acceleration, and using the graph to determine the car's speed changes at specific times.
🏃♂️ Runners' Velocity and Acceleration Comparison
The sixth paragraph compares the motion of two runners on a racetrack, with one runner's velocity represented by a graph and the other's by an equation. The tasks involve finding the velocity and acceleration of each runner at a specific time and understanding their motion. The summary explains how to read the velocity from the graph, calculate the velocity using the given equation, and determine acceleration by analyzing the slope of the velocity graph and differentiating the velocity equation.
🌐 Trigonometric Velocity Function Analysis
The seventh paragraph examines an object's motion along the x-axis with a velocity function involving a trigonometric expression. The discussion includes finding the acceleration of the object at a specific time and considering two statements about the object's velocity and speed between certain times. The summary details the process of deriving the acceleration function from the velocity function, evaluating it at a given time, and analyzing the statements based on the signs of velocity and acceleration to determine the correctness of each.
📊 Velocity and Speed Analysis with Trigonometric Functions
The final paragraph delves into the analysis of an object's velocity and speed using a trigonometric function. It involves solving for when the velocity is zero, determining the intervals where the velocity and acceleration have the same or opposite signs, and evaluating statements about the object's speed. The summary highlights the mathematical approach to finding critical values for the velocity function, analyzing the intervals of motion, and understanding the physical implications of the velocity and acceleration signs on the object's speed.
Mindmap
Keywords
💡Position Function
💡Velocity
💡Piecewise Function
💡Acceleration
💡Average Velocity
💡Direction Change
💡Sign Change
💡Derivative
💡Continuous Function
💡Rolle's Theorem
💡Trigonometric Functions
Highlights
The video discusses unit 5 homework problems 29 through 35 involving the analysis of a particle's motion along the x-axis.
For problem 29, the particle moves to the right when the velocity is positive, identified by the increasing position graph from 0 to 1 second.
The particle moves to the left during intervals where the position graph decreases, specifically from 2 to 3 and 5 to 6 seconds.
Velocity is expressed as a piecewise function with different slopes corresponding to intervals of time and position graph changes.
Endpoints and corner points where the position is not differentiable result in undefined velocities.
For problem 30, the particle's velocity changes direction multiple times within the interval from 0 to 5 seconds, identified by the velocity graph's sign changes.
The velocity function V(t) involves a combination of a polynomial and trigonometric function, which complicates the analysis of direction changes.
At t equals 2, the particle is momentarily at rest with zero velocity but does not change direction, as indicated by the velocity graph.
Problem 31 involves calculating the average acceleration between t equals 1 and t equals 3.5 seconds using the velocity function.
The average acceleration is found by the change in velocity over the change in time, resulting in approximately 0.84 meters per second squared.
In problem 32, Jeff's bicycle velocity is analyzed on a graph, with the slope at t equals 4 minutes indicating a decrease in velocity.
Rolle's Theorem is discussed in the context of finding intervals where acceleration equals zero, but it does not apply due to non-differentiability points.
The particle's motion involves a change in direction after forgetting something at home, which is represented by a change from positive to negative velocity.
Problem 33 examines the car's acceleration from a velocity graph, identifying intervals of positive acceleration and calculating average acceleration.
The car's speed is analyzed for increasing or decreasing intervals, with the velocity graph indicating a decrease at t equals 40 seconds.
In problem 34, the velocities of two runners are compared at t equals 2 seconds using both a graph and an equation, revealing different methods for determining speed.
Acceleration for both runners is calculated at t equals 2 seconds, with runner B's acceleration determined through differentiation of the velocity equation.
Problem 35 involves an object's motion with a velocity function based on a sine function, leading to an acceleration function derived using calculus.
The acceleration of the object at t equals 4 is negative, indicating the object is slowing down, which is confirmed by the velocity and acceleration having opposite signs.
Statements regarding the object's velocity and speed changes between t equals 3 and 4.5 seconds are evaluated, with one being true and the other false due to the signs of velocity and acceleration.
Transcripts
Browse More Related Video

Calculus AB Homework 5.3: Position, Velocity, Acceleration

Calculus AB Unit 5 Review: Particle Motion

Rectilinear Motion or Particle Motion or Straight Line Motion!

Average Acceleration and Instantaneous Acceleration
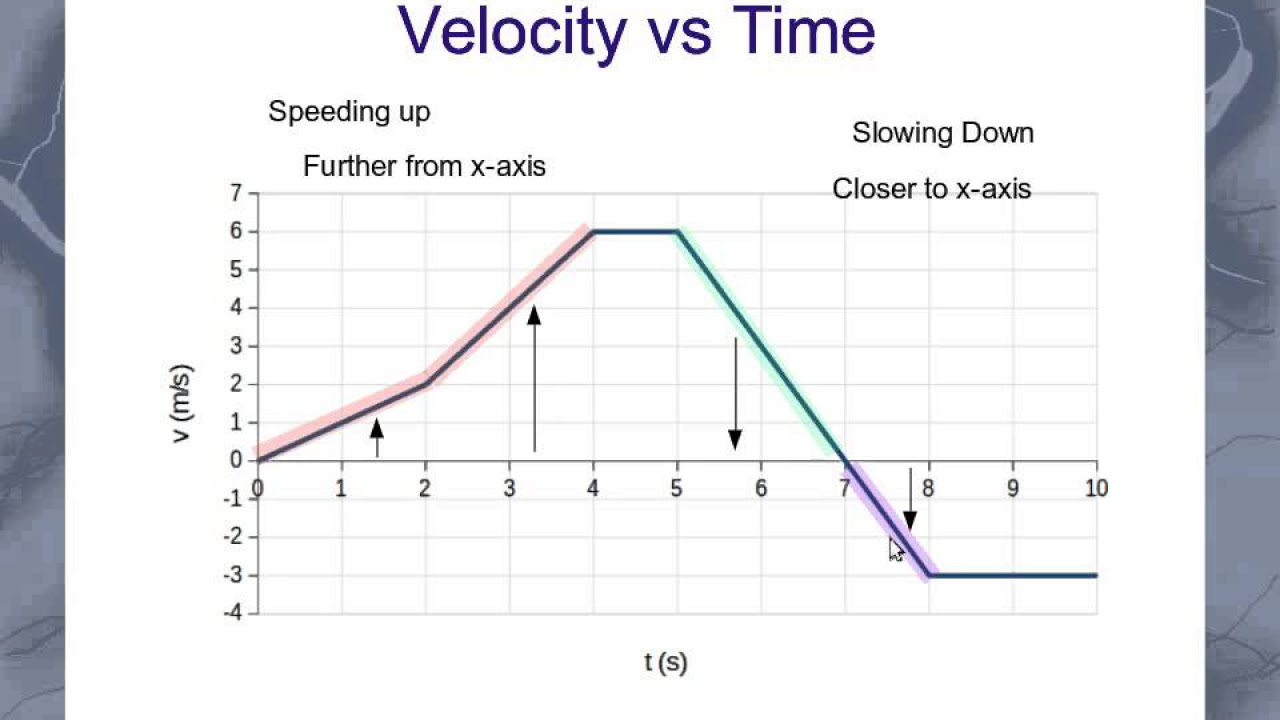
Interpreting Velocity graphs
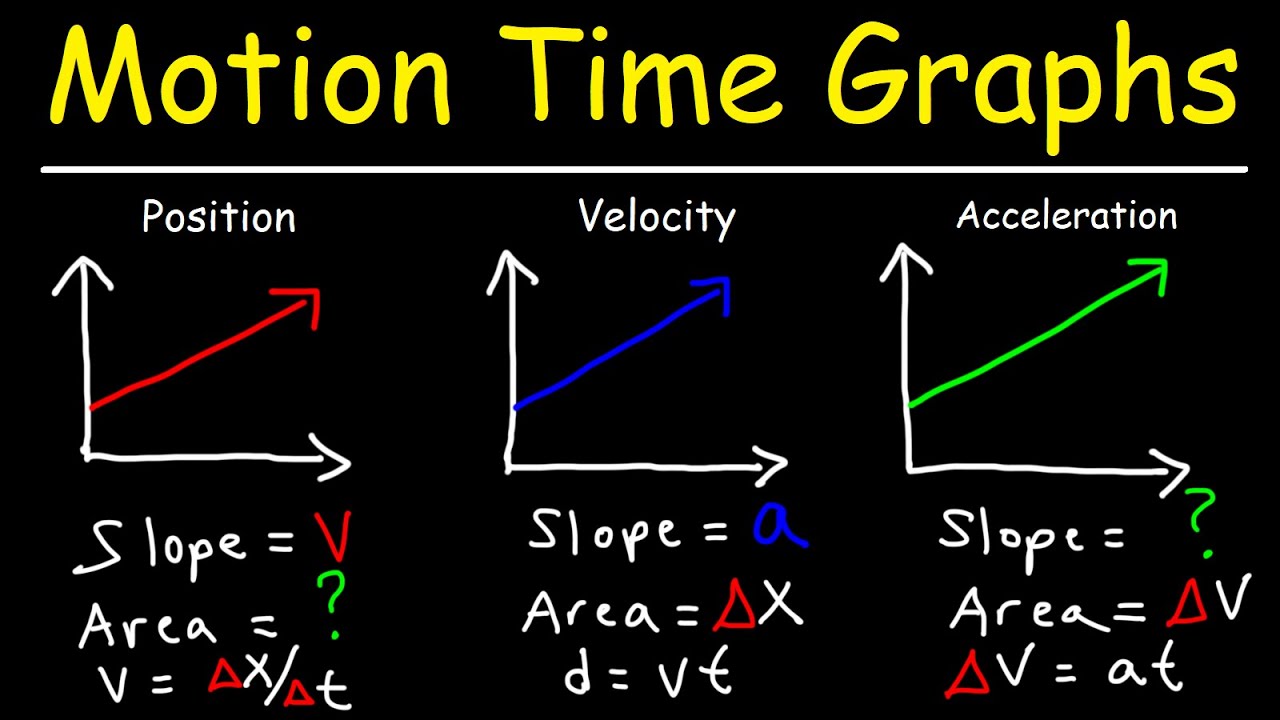
Velocity Time Graphs, Acceleration & Position Time Graphs - Physics
5.0 / 5 (0 votes)
Thanks for rating: